Inclusion Exclusion principle and programming applications

Sum Rule – If a task can be done in one of n₁ ways or one of n₂ ways, where none of the set of n₁ ways is the same as any of the set of n₂ ways, then there are n₁ + n₂ ways to do the task. The sum-rule mentioned above states that if there are multiple sets of ways of doing a task, there shouldn’t be any way that is common between two sets of ways because if there is, it would be counted twice and the enumeration would be wrong. 

The principle of inclusion-exclusion says that in order to count only unique ways of doing a task, we must add the number of ways to do it in one way and the number of ways to do it in another and then subtract the number of ways to do the task that are common to both sets of ways. 

The principle of inclusion-exclusion is also known as the subtraction principle. For two sets of ways A_iand  A₂, the enumeration would like- 
| A₁ ∪ A₂  |= |A₁ |+ | A₂| – |A₁ ∩ A₂|

Below are some examples to explain the application of inclusion-exclusion principle:  

Example 1: How many binary strings of length 8 either start with a ‘1’ bit or end with two bits ’00’? 

Solution: If the string starts with one, there are 7 characters left which can be filled in 2⁷ = 128 ways. 
If the string ends with ’00’ then 6 characters can be filled in 2 ⁶ = 64 ways. 

Now if we add the above sets of ways and conclude that it is the final answer, then it would be wrong. This is because there are strings with start with ‘1’ and end with ’00’ both, and since they satisfy both criteria they are counted twice. 
So we need to subtract such strings to get a correct count. 
Strings that start with ‘1’ and end with ’00’ have five characters that can be filled in 2⁵=32 ways. 
So by the inclusion-exclusion principle we get- Total strings = 128 + 64 – 32 = 160 

Example 2: How many numbers between 1 and 1000, including both, are divisible by 3 or 4? 
Solution: Number of numbers divisible by 3 =

= 

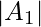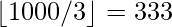
. Number of numbers divisible by 4 =
= 

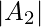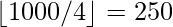
.Number of numbers divisible by 3 and 4 =
= 

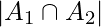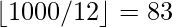
Therefore, number of numbers divisible by 3 or 4 =
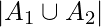 = 333 + 250 – 83 = 500 

Implementation

Problem 1: How many numbers between 1 and 1000, including both, are divisible by 3 or 4? 
The Approach will be the one discussed above, we add the number of numbers that are divisible by 3 and 4 and subtract the numbers which are divisible by 12. 

C++

// CPP program to count the
// number of numbers between
// 1 and 1000, including both,
// that are divisible by 3 or 4
#include <bits/stdc++.h>
using namespace std;

// function to count the divisors
int countDivisors(int N, int a, int b)
{
    // Counts of numbers
    // divisible by a and b
    int count1 = N / a;
    int count2 = N / b;

    // inclusion-exclusion
    // principle applied
    int count3 = (N / (a * b));

    return count1 + count2 - count3;
}

// Driver Code
int main()
{
    int N = 1000, a = 3, b = 4;
    cout << countDivisors(N, a, b);
    return 0;
}

Java

// Java program to count the
// number of numbers between
// 1 and 1000, including both,
// that are divisible by 3 or 4
import java.io.*;

class GFG {

    // function to count the divisors
    public static int countDivisors(int N, int a, int b)
    {
        // Counts of numbers
        // divisible by a and b
        int count1 = N / a;
        int count2 = N / b;

        // inclusion-exclusion
        // principle applied
        int count3 = (N / (a * b));

        return count1 + count2 - count3;
    }

    // Driver Code
    public static void main(String[] args)
    {
        int N = 1000, a = 3, b = 4;
        System.out.println(countDivisors(N, a, b));
    }
}

// This code is contributed by m_kit

Python3

# Python3 program to count the
# number of numbers between
# 1 and 1000, including both,
# that are divisible by 3 or 4

# function to count the divisors


def countDivisors(N, a, b):

    # Counts of numbers
    # divisible by a and b
    count1 = N // a
    count2 = N // b

    # inclusion-exclusion
    # principle applied
    count3 = (N // (a * b))

    return count1 + count2 - count3


# Driver Code
N = 1000
a = 3
b = 4
print(countDivisors(N, a, b))

# This code is contributed by shubhamsingh10

C#

// C# program to count the
// number of numbers between
// 1 and 1000, including both,
// that are divisible by 3 or 4
using System;

class GFG {

    // function to count
    // the divisors
    public static int countDivisors(int N, int a, int b)
    {
        // Counts of numbers
        // divisible by a and b
        int count1 = N / a;
        int count2 = N / b;

        // inclusion-exclusion
        // principle applied
        int count3 = (N / (a * b));

        return count1 + count2 - count3;
    }

    // Driver Code
    static public void Main()
    {
        int N = 1000, a = 3, b = 4;
        Console.WriteLine(countDivisors(N, a, b));
    }
}

// This code is contributed by aj_36

PHP

<?php
// PHP program to count the
// number of numbers between
// 1 and 1000, including both,
// that are divisible by 3 or 4

// function to count the divisors
function countDivisors($N, $a, $b)
{
    // Counts of numbers
    // divisible by a and b
    $count1 = $N / $a;
    $count2 = $N / $b;

    // inclusion-exclusion
    // principle applied
    $count3 = ($N / ($a * $b));

    return $count1 + $count2 - $count3;
}

// Driver Code
$N = 1000; $a = 3; $b = 4;
echo countDivisors($N, $a, $b);

// This code is contributed by aj_36
?>

Javascript

<script>

    // Javascript program to count the
    // number of numbers between
    // 1 and 1000, including both,
    // that are divisible by 3 or 4

    // function to count
    // the divisors
    function countDivisors(N, a, b)
    {
        // Counts of numbers
        // divisible by a and b
        let count1 = parseInt(N / a, 10);
        let count2 = parseInt(N / b, 10);

        // inclusion-exclusion
        // principle applied
        let count3 = parseInt(N / (a * b), 10);

        return count1 + count2 - count3;
    }

    let N = 1000, a = 3, b = 4;
      document.write(countDivisors(N, a, b));

</script>

Output :

500

Problem 2: Given N prime numbers and a number M, find out how many numbers from 1 to M are divisible by any of the N given prime numbers. 

Examples :

Input: N numbers = {2, 3, 5, 7}   M = 100 
Output: 78   

Input: N numbers = {2, 5, 7, 11}   M = 200
Output: 137

The approach for this problem will be to generate all the possible combinations of numbers using N prime numbers using power set in 2^N. For each of the given prime numbers P_i among N, it has M/P_i multiples. Suppose M=10, and we are given with 3 prime numbers(2, 3, 5), then the total count of multiples when we do 10/2 + 10/3 + 10/5 is 11. Since we are counting 6 and 10 twice, the count of multiples in range 1-M comes 11. Using inclusion-exclusion principle, we can get the correct number of multiples. The inclusion-exclusion principle for three terms can be described as: 

Similarly, for every N numbers, we can easily find the total number of multiples in range 1 to M by applying the formula for an intersection of N numbers. The numbers that are formed by multiplication of an odd number of prime numbers will be added and the numbers formed by multiplication of even numbers will thus be subtracted to get the total number of multiples in the range 1 to M.

Using power set we can easily get all the combination of numbers formed by the given prime numbers. To know if the number is formed by multiplication of odd or even numbers, simply count the number of set bits in all the possible combinations (1-1<<N).
Using power sets and adding the numbers created by combinations of odd and even prime numbers we get 123 and 45 respectively. Using inclusion-exclusion principle we get the number of numbers in range 1-M that is divided by any one of N prime numbers is (odd combinations-even combinations) = (123-45) = 78.

Below is the implementation of the above idea: 

C++

// CPP program to count the
// number of numbers in range
// 1-M that are divisible by
// given N prime numbers
#include <bits/stdc++.h>
using namespace std;

// function to count the number
// of numbers in range 1-M that
// are divisible by given N
// prime numbers
int count(int a[], int m, int n)
{
    int odd = 0, even = 0;
    int counter, i, j, p = 1;
    int pow_set_size = (1 << n);

    // Run from counter 000..0 to 111..1
    for (counter = 1; counter < pow_set_size; counter++) {
        p = 1;
        for (j = 0; j < n; j++) {

            // Check if jth bit in the
            // counter is set If set
            // then print jth element from set
            if (counter & (1 << j)) {
                p *= a[j];
            }
        }

        // if set bits is odd, then add to
        // the number of multiples
        if (__builtin_popcount(counter) & 1)
            odd += (m / p);
        else
            even += (m / p);
    }

    return odd - even;
}

// Driver Code
int main()
{
    int a[] = { 2, 3, 5, 7 };
    int m = 100;
    int n = sizeof(a) / sizeof(a[0]);
    cout << count(a, m, n);
    return 0;
}

Java

// Java program to count the
// number of numbers in range
// 1-M that are divisible by
// given N prime numbers

import java.io.*;

class GFG {
    // function to count the number
    // of numbers in range 1-M that
    // are divisible by given N
    // prime numbers
    public static int count(int a[], int m, int n)
    {
        int odd = 0;
        int even = 0;
        int counter = 0;
        int i = 0;
        int j = 0;
        int p = 1;
        int pow_set_size = (1 << n);

        // Run from counter 000..0 to 111..1
        for (counter = 1; counter < pow_set_size;
             counter++) {
            p = 1;
            for (j = 0; j < n; j++) {
                // Check if jth bit in the
                // counter is set If set
                // then print jth element from set
                if ((counter & (1 << j)) > 0) {
                    p *= a[j];
                }
            }

            // if set bits is odd, then add to
            // the number of multiples
            if (Integer.bitCount(counter) % 2 == 1) {
                odd += (m / p);
            }
            else {
                even += (m / p);
            }
        }

        return odd - even;
    }

    // Driver Code
    public static void main(String[] args)
    {
        int a[] = { 2, 3, 5, 7 };
        int m = 100;
        int n = a.length;
        System.out.println(count(a, m, n));
    }
}

Python3

# Python3 program to count the
# number of numbers in range
# 1-M that are divisible by
# given N prime numbers


def bitsoncount(x):
    return bin(x).count('1')

# function to count the number
# of numbers in range 1-M that
# are divisible by given N
# prime numbers


def count(a, m, n):

    odd = 0
    even = 0
    p = 1
    pow_set_size = 1 << n

    # Run from counter 000..0 to 111..1
    for counter in range(1, pow_set_size):

        p = 1
        for j in range(n):

            # Check if jth bit in the
            # counter is set If set
            # then print jth element from set
            if (counter & (1 << j)):

                p *= a[j]

        # if set bits is odd, then add to
        # the number of multiples
        if (bitsoncount(counter) & 1):
            odd += (m // p)
        else:

            even += (m // p)

    return odd - even


# Driver Code
a = [2, 3, 5, 7]
m = 100
n = len(a)
print(count(a, m, n))

# This code is contributed by shivanisinghss2110

C#

using System;

// C# program to count the
// number of numbers in range
// 1-M that are divisible by
// given N prime numbers
class GFG {

  public static int bitCount(int n)
  {
    int count = 0;
    while (n != 0)
    {
      count++;
      n &= (n - 1);
    }
    return count;
  }

  // function to count the number
  // of numbers in range 1-M that
  // are divisible by given N
  // prime numbers
  public static int count(int[] a, int m, int n)
  {
    int odd = 0, even = 0;
    int counter, i, j, p = 1;
    int pow_set_size = (1 << n);

    // Run from counter 000..0 to 111..1
    for (counter = 1; counter < pow_set_size; counter++) {
      p = 1;
      for (j = 0; j < n; j++) {

        // Check if jth bit in the
        // counter is set If set
        // then print jth element from set
        if ((counter & (1 << j)) != 0) {
          p = p * a[j];
        }
      }

      // if set bits is odd, then add to
      // the number of multiples
      if ((bitCount(counter) & 1) != 0)
        odd += (m / p);
      else
        even += (m / p);
    }

    return odd - even;
  }

  // Driver code
  static void Main() {
    int[] a = { 2, 3, 5, 7 };
    int m = 100;
    int n = a.Length;
    System.Console.WriteLine(count(a, m, n));
  }
}

// The  code is given by Gautam goel.

Javascript

<script>

// Javascript program to count the
// number of numbers in range
// 1-M that are divisible by
// given N prime numbers

// Bit count
function bitCount(n)
{
    n = n - ((n >> 1) & 0x55555555)
    n = (n & 0x33333333) +
        ((n >> 2) & 0x33333333)
    return ((n + (n >> 4) & 0xF0F0F0F) *
         0x1010101) >> 24
}

// Function to count the number
// of numbers in range 1-M that
// are divisible by given N
// prime numbers
function count(a, m, n)
{
    var odd = 0;
    var even = 0;
    var counter = 0;
    var i = 0;
    var j = 0;
    var p = 1;
    var pow_set_size = (1 << n);

    // Run from counter 000..0 to 111..1
    for(counter = 1;
        counter < pow_set_size;
        counter++)
    {
        p = 1;
        for(j = 0; j < n; j++)
        {

            // Check if jth bit in the
            // counter is set If set
            // then print jth element from set
            if ((counter & (1 << j)) > 0)
            {
                p *= a[j];
            }
        }

        // If set bits is odd, then add to
        // the number of multiples
        if (bitCount(counter) % 2 == 1)
        {
            odd += parseInt(m / p);
        }
        else
        {
            even += parseInt(m / p);
        }
    }
    return odd - even;
}

// Driver Code
var a = [ 2, 3, 5, 7 ];
var m = 100;
var n = a.length;

document.write(count(a, m, n));

// This code is contributed by Rajput-Ji

</script>

Output:

78

Time Complexity: O(2^N*N)