Line detection in python with OpenCV | Houghline method

The Hough Transform is a method that is used in image processing to detect any shape, if that shape can be represented in mathematical form. It can detect the shape even if it is broken or distorted a little bit. 
We will see how Hough transform works for line detection using the HoughLine transform method. To apply the Houghline method, first an edge detection of the specific image is desirable. For the edge detection technique go through the article Edge detection 

Basics of Houghline Method

A line can be represented as y = mx + c or in parametric form, as r = xcos? + ysin? where r is the perpendicular distance from origin to the line, and ? is the angle formed by this perpendicular line and horizontal axis measured in counter-clockwise ( That direction varies on how you represent the coordinate system. This representation is used in OpenCV). 

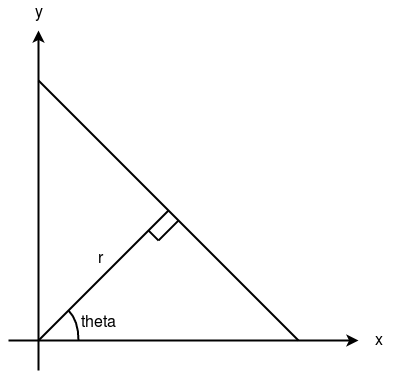
So Any line can be represented in these two terms, (r, ?).
Working of Houghline method:

• First it creates a 2D array or accumulator (to hold values of two parameters) and it is set to zero initially.
• Let rows denote the r and columns denote the (?)theta.
• Size of array depends on the accuracy you need. Suppose you want the accuracy of angles to be 1 degree, you need 180 columns(Maximum degree for a straight line is 180).
• For r, the maximum distance possible is the diagonal length of the image. So taking one pixel accuracy, number of rows can be diagonal length of the image.

Example:
Consider a 100×100 image with a horizontal line at the middle. Take the first point of the line. You know its (x,y) values. Now in the line equation, put the values ?(theta) = 0,1,2,….,180 and check the r you get. For every (r, ?) pair, you increment value by one in the accumulator in its corresponding (r, ?) cells. So now in accumulator, the cell (50,90) = 1 along with some other cells. 
Now take the second point on the line. Do the same as above. Increment the values in the cells corresponding to (r, ?) you got. This time, the cell (50,90) = 2. We are actually voting the (r, ?) values. You continue this process for every point on the line. At each point, the cell (50,90) will be incremented or voted up, while other cells may or may not be voted up. This way, at the end, the cell (50,90) will have maximum votes. So if you search the accumulator for maximum votes, you get the value (50,90) which says, there is a line in this image at distance 50 from origin and at angle 90 degrees. 

Everything explained above is encapsulated in the OpenCV function, cv2.HoughLines(). It simply returns an array of (r, 0) values. r is measured in pixels and 0 is measured in radians. 

Python

# Python program to illustrate HoughLine
# method for line detection
import cv2
import numpy as np

# Reading the required image in
# which operations are to be done.
# Make sure that the image is in the same
# directory in which this python program is
img = cv2.imread('image.jpg')

# Convert the img to grayscale
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

# Apply edge detection method on the image
edges = cv2.Canny(gray, 50, 150, apertureSize=3)

# This returns an array of r and theta values
lines = cv2.HoughLines(edges, 1, np.pi/180, 200)

# The below for loop runs till r and theta values
# are in the range of the 2d array
for r_theta in lines:
    arr = np.array(r_theta[0], dtype=np.float64)
    r, theta = arr
    # Stores the value of cos(theta) in a
    a = np.cos(theta)

    # Stores the value of sin(theta) in b
    b = np.sin(theta)

    # x0 stores the value rcos(theta)
    x0 = a*r

    # y0 stores the value rsin(theta)
    y0 = b*r

    # x1 stores the rounded off value of (rcos(theta)-1000sin(theta))
    x1 = int(x0 + 1000*(-b))

    # y1 stores the rounded off value of (rsin(theta)+1000cos(theta))
    y1 = int(y0 + 1000*(a))

    # x2 stores the rounded off value of (rcos(theta)+1000sin(theta))
    x2 = int(x0 - 1000*(-b))

    # y2 stores the rounded off value of (rsin(theta)-1000cos(theta))
    y2 = int(y0 - 1000*(a))

    # cv2.line draws a line in img from the point(x1,y1) to (x2,y2).
    # (0,0,255) denotes the colour of the line to be
    # drawn. In this case, it is red.
    cv2.line(img, (x1, y1), (x2, y2), (0, 0, 255), 2)

# All the changes made in the input image are finally
# written on a new image houghlines.jpg
cv2.imwrite('linesDetected.jpg', img)

Elaboration of function(cv2.HoughLines (edges,1,np.pi/180, 200)):

1. First parameter, Input image should be a binary image, so apply threshold edge detection before finding applying hough transform.
2. Second and third parameters are r and ?(theta) accuracies respectively.
3. Fourth argument is the threshold, which means minimum vote it should get for it to be considered as a line.
4. Remember, number of votes depend upon number of points on the line. So it represents the minimum length of line that should be detected. 
   

Alternate simpler method for directly extracting points:

Python3

import cv2
import numpy as np

# Read image
image = cv2.imread('path/to/image.png')

# Convert image to grayscale
gray = cv2.cvtColor(image,cv2.COLOR_BGR2GRAY)

# Use canny edge detection
edges = cv2.Canny(gray,50,150,apertureSize=3)

# Apply HoughLinesP method to
# to directly obtain line end points
lines_list =[]
lines = cv2.HoughLinesP(
            edges, # Input edge image
            1, # Distance resolution in pixels
            np.pi/180, # Angle resolution in radians
            threshold=100, # Min number of votes for valid line
            minLineLength=5, # Min allowed length of line
            maxLineGap=10 # Max allowed gap between line for joining them
            )

# Iterate over points
for points in lines:
      # Extracted points nested in the list
    x1,y1,x2,y2=points[0]
    # Draw the lines joing the points
    # On the original image
    cv2.line(image,(x1,y1),(x2,y2),(0,255,0),2)
    # Maintain a simples lookup list for points
    lines_list.append([(x1,y1),(x2,y2)])

# Save the result image
cv2.imwrite('detectedLines.png',image)

Summarizing the process

• In an image analysis context, the coordinates of the point(s) of edge segments (i.e. X,Y ) in the image are known and therefore serve as constants in the parametric line equation, while R(rho) and Theta(?) are the unknown variables we seek.
• If we plot the possible (r) values defined by each (theta), points in cartesian image space map to curves (i.e. sinusoids) in the polar Hough parameter space. This point-to-curve transformation is the Hough transformation for straight lines.
• The transform is implemented by quantizing the Hough parameter space into finite intervals or accumulator cells. As the algorithm runs, each (X,Y) is transformed into a discretized (r,0) curve and the accumulator(2D array) cells which lie along this curve are incremented.
• Resulting peaks in the accumulator array represent strong evidence that a corresponding straight line exists in the image.

Applications of Hough transform:

1. It is used to isolate features of a particular shape within an image.
2. Tolerant of gaps in feature boundary descriptions and is relatively unaffected by image noise.
3. Used extensively in barcode scanning, verification and recognition

If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.