Length of the chord of the circle whose radius and the angle subtended at the center by the chord is given
Last Updated :
07 Jun, 2022
Given a circle whose radius and the angle subtended at the centre by its chord is given. The task is to find the length of the chord.
Examples:
Input: r = 4, x = 63
Output: 4.17809
Input:: r = 9, x = 71
Output:: 10.448
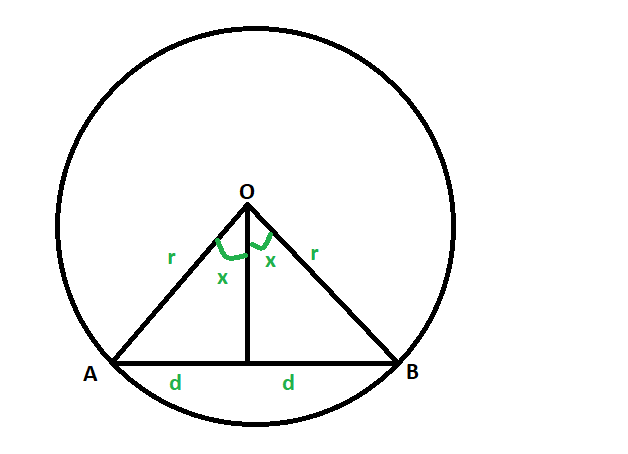
Approach:
- Let the circle has center at O and has radius r, and it’s chord be AB.
- length of the chord be 2d, and the angle subtended by it on the center be 2x degrees.
- As the perpendicular dropped at the chord bisects the chord so, the perpendicular also equally divides the subtended angle 2x in x degrees.
- So, from the diagram,
d/r = sin(x*π/180)(here x deg is converted in radians) - So, d = rsin(x*π/180)
therefore, 2d = 2rsin(x*π/180)
- So,
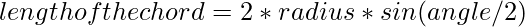
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void length_of_chord(double r, double x)
{
cout << "The length of the chord"
<< " of the circle is "
<< 2 * r * sin(x * (3.14 / 180))
<< endl;
}
int main()
{
double r = 4, x = 63;
length_of_chord(r, x);
return 0;
}
|
Java
class GFG
{
static void length_of_chord(double r, double x)
{
System.out.println("The length of the chord"
+ " of the circle is "
+ 2 * r * Math.sin(x * (3.14 / 180)));
}
public static void main(String[] args)
{
double r = 4, x = 63;
length_of_chord(r, x);
}
}
|
Python3
import math as mt
def length_of_chord(r, x):
print("The length of the chord"
," of the circle is "
,2 * r * mt.sin(x * (3.14 / 180)))
r = 4
x = 63;
length_of_chord(r, x)
|
C#
using System;
class GFG
{
static void length_of_chord(double r, double x)
{
Console.WriteLine("The length of the chord" +
" of the circle is " +
2 * r * Math.Sin(x * (3.14 / 180)));
}
public static void Main(String[] args)
{
double r = 4, x = 63;
length_of_chord(r, x);
}
}
|
PHP
<?php
function length_of_chord($r, $x)
{
echo "The length of the chord",
" of the circle is "
,2 * $r * sin($x * (3.14 / 180)) ;
}
$r = 4; $x = 63;
length_of_chord($r, $x);
?>
|
Javascript
<script>
function length_of_chord(r, x)
{
document.write("The length of the chord"
+ " of the circle is "
+ 2 * r * Math.sin(x * (3.14 / 180))
+ "<br>");
}
let r = 4, x = 63;
length_of_chord(r, x);
</script>
|
Output: The length of the chord of the circle is 7.12603
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...