Length of the perpendicular bisector of the line joining the centers of two circles
Last Updated :
03 Aug, 2022
Given are two circles whose radii are given, such that the smaller lies completely within the bigger circle, and they touch each other at one point. We have to find the length of the perpendicular bisector of the line joining the centres of the circles.
Examples:
Input: r1 = 5, r2 = 3
Output: 9.79796
Input: r1 = 8, r2 = 4
Output: 15.4919
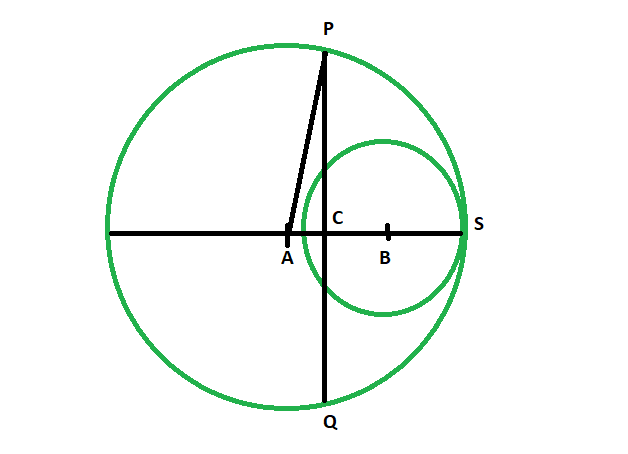
Approach:
- Let the two circles have center at A and B.The perpendicular bisector PQ, bisects the line at C.
- Let radius of bigger circle = r1
radius of smaller circle = r2
- so, AB = r1-r2,
- therefore, AC = (r1-r2)/2
- In, the figure, we see
PA = r1
- in triangle ACP,
PC^2 + AC^2 = PA^2
PC^2 = PA^2 – AC^2
PC^2 = r1^2 – (r1-r2)^2/4
- so, PQ = 2*√(r1^2 – (r1-r2)^2/4)
Length of the perpendicular bisector = 2 * sqrt(r1^2 – (r1-r2)*(r1-r2)/4)
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void lengperpbisect(double r1, double r2)
{
double z = 2 * sqrt((r1 * r1)
- ((r1 - r2)
* (r1 - r2) / 4));
cout << "The length of the "
<< "perpendicular bisector is "
<< z << endl;
}
int main()
{
double r1 = 5, r2 = 3;
lengperpbisect(r1, r2);
return 0;
}
|
Java
class GFG {
static void lengperpbisect(double r1, double r2)
{
double z = 2 * Math.sqrt((r1 * r1)
- ((r1 - r2)
* (r1 - r2) / 4));
System.out.println("The length of the "
+ "perpendicular bisector is "
+ z );
}
public static void main(String[] args)
{
double r1 = 5, r2 = 3;
lengperpbisect(r1, r2);
}
}
|
Python3
def lengperpbisect(r1, r2):
z = 2 * (((r1 * r1) - ((r1 - r2) * (r1 - r2) / 4))**(1/2));
print("The length of the perpendicular bisector is ", z);
r1 = 5; r2 = 3;
lengperpbisect(r1, r2);
|
C#
using System;
class GFG
{
static void lengperpbisect(double r1, double r2)
{
double z = 2 * Math.Sqrt((r1 * r1)
- ((r1 - r2)
* (r1 - r2) / 4));
Console.WriteLine("The length of the "
+ "perpendicular bisector is "
+ z );
}
public static void Main()
{
double r1 = 5, r2 = 3;
lengperpbisect(r1, r2);
}
}
|
Javascript
<script>
function lengperpbisect(r1 , r2)
{
var z = 2 * Math.sqrt((r1 * r1)
- ((r1 - r2)
* (r1 - r2) / 4));
document.write("The length of the "
+ "perpendicular bisector is "
+ z.toFixed(5) );
}
var r1 = 5, r2 = 3;
lengperpbisect(r1, r2);
</script>
|
Output:
The length of the perpendicular bisector is 9.79796
Time Complexity: O(log(n)), since using inbuilt sqrt function
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...