Radii of the three tangent circles of equal radius which are inscribed within a circle of given radius
Last Updated :
11 Sep, 2023
Given here is a circle of a given radius. Inside it, three tangent circles of equal radius are inscribed. The task is to find the radii of these tangent circles.
Examples:
Input: R = 4
Output: 1.858
Input: R = 11
Output: 5.1095
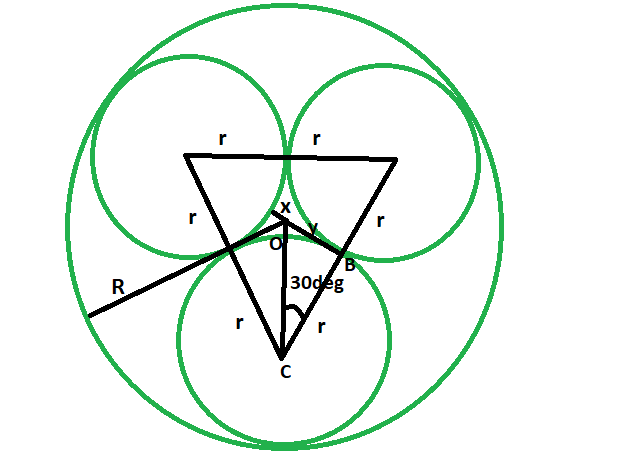
Approach:
Let the radii of the tangent circles be r, and the radius of the circumscribing circle
is R.x is the smaller distance from the circumference of the tangent circle and the center of the circumscribing circle.
From the diagram, it is very clear,
2r + x = R
- now in triangle OBC,
cos 30 = r/(r+x)
rcos30 + xcos30 = r
x = r(1-cos30)/cos30
- also, x = R-2r
- So,
R-2r = r(1-cos30)/cos30
R-2r = 0.133r/0.867
R-2r = 0.153r
R = 2.153r
so, r = 0.4645R
Radii of three tangent circles = 0.4645*radius of the circumscribed circle
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void threetangcircle(int R)
{
cout << "The radii of the tangent circles is "
<< 0.4645 * R << endl;
}
int main()
{
int R = 4;
threetangcircle(R);
return 0;
}
|
Java
import java.io.*;
class GFG {
static void threetangcircle(int R)
{
System.out.print(
"The radii of the tangent circles is "
+ 0.4645 * R);
}
public static void main(String[] args)
{
int R = 4;
threetangcircle(R);
}
}
|
Python3
def threetangcircle(R):
print("The radii of the tangent",
"circles is ", end="")
print(0.4645 * R)
R = 4
threetangcircle(R)
|
C#
using System;
class GFG {
static void threetangcircle(int R)
{
Console.WriteLine(
"The radii of the tangent circles is "
+ 0.4645 * R);
}
public static void Main()
{
int R = 4;
threetangcircle(R);
}
}
|
Javascript
<script>
function threetangcircle(R)
{
document.write("The radii of the tangent circles is "
+ 0.4645 * R);
}
var R = 4;
threetangcircle(R);
</script>
|
PHP
<?php
function threetangcircle($R)
{
echo "The radii of the tangent circles is ",
( 0.4645 * $R );
}
$R = 4;
threetangcircle($R);
?>
|
Output
The radii of the tangent circles is 1.858
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...