Shortest distance from the center of a circle to a chord
Last Updated :
26 Nov, 2022
Given a circle which has a chord inside it. The length of the chord and the radius of the circle are given. The task is to find the shortest distance from the chord to the center.
Examples:
Input: r = 4, d = 3
Output: 3.7081
Input: r = 9.8, d = 7.3
Output: 9.09492
Approach:
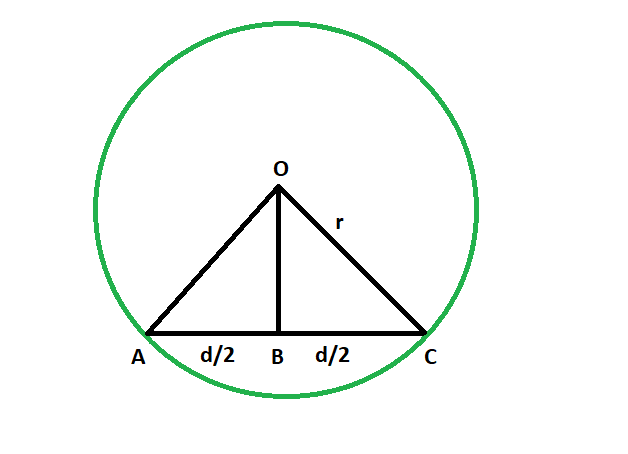
- We know that the line segment that is dropped from the center on the chord bisects the chord. The line is the perpendicular bisector of the chord, and we know the perpendicular distance is the shortest distance, so our task is to find the length of this perpendicular bisector.
- let radius of the circle = r
- length of the chord = d
- so, in triangle OBC,
from Pythagoras theorem,
OB^2 + (d/2)^2 = r^2
so, OB = √(r^2 – d^2/4) - So,
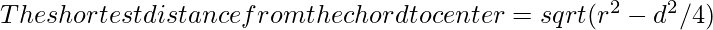
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void shortdis(double r, double d)
{
cout << "The shortest distance "
<< "from the chord to center "
<< sqrt((r * r) - ((d * d) / 4))
<< endl;
}
int main()
{
double r = 4, d = 3;
shortdis(r, d);
return 0;
}
|
Java
class GFG
{
static void shortdis(double r, double d)
{
System.out.println("The shortest distance "
+ "from the chord to center "
+ (Math.sqrt((r * r) - ((d * d) / 4))));
}
public static void main(String[] args)
{
double r = 4, d = 3;
shortdis(r, d);
}
}
|
Python3
def shortdis(r, d):
print("The shortest distance ",end="");
print("from the chord to center ",end="");
print(((r * r) - ((d * d) / 4))**(1/2));
r = 4;
d = 3;
shortdis(r, d);
|
C#
using System;
class GFG
{
static void shortdis(double r, double d)
{
Console.WriteLine("The shortest distance "
+ "from the chord to center "
+ (Math.Sqrt((r * r) - ((d * d) / 4))));
}
public static void Main()
{
double r = 4, d = 3;
shortdis(r, d);
}
}
|
PHP
<?php
function shortdis($r, $d)
{
echo "The shortest distance ";
echo "from the chord to center ";
echo sqrt(($r * $r) - (($d * $d) / 4));
}
$r = 4;
$d = 3;
shortdis($r, $d);
?>
|
Javascript
<script>
function shortdis(r, d)
{
document.write("The shortest distance "
+ "from the chord to center "
+ Math.sqrt((r * r) - ((d * d) / 4))
+ "<br>");
}
let r = 4, d = 3;
shortdis(r, d);
</script>
|
OutputThe shortest distance from the chord to center 3.7081
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...