Tree Traversal Techniques – Data Structure and Algorithm Tutorials
Last Updated :
29 Apr, 2024
Tree Traversal techniques include various ways to visit all the nodes of the tree. Unlike linear data structures (Array, Linked List, Queues, Stacks, etc) which have only one logical way to traverse them, trees can be traversed in different ways. In this article, we will discuss about all the tree traversal techniques along with their uses.
.webp)
Tree Traversal Meaning:
Tree Traversal refers to the process of visiting or accessing each node of the tree exactly once in a certain order. Tree traversal algorithms help us to visit and process all the nodes of the tree. Since tree is not a linear data structure, there are multiple nodes which we can visit after visiting a certain node. There are multiple tree traversal techniques which decide the order in which the nodes of the tree are to be visited.
Tree Traversal Techniques:
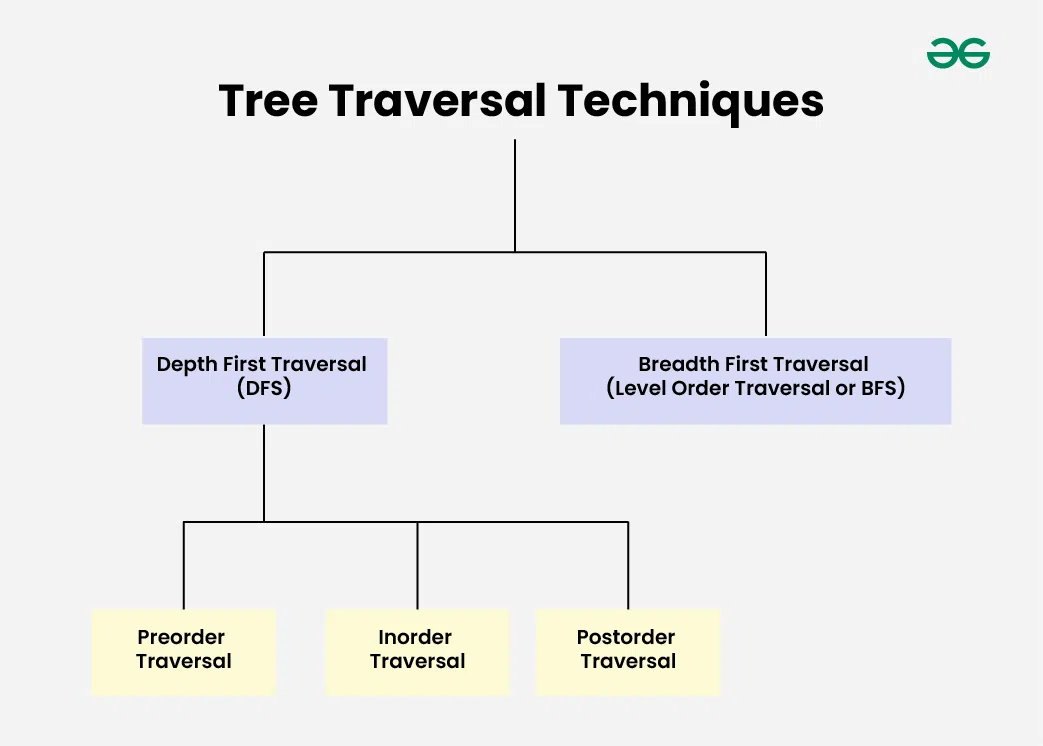
A Tree Data Structure can be traversed in following ways:
- Depth First Search or DFS
- Inorder Traversal
- Preorder Traversal
- Postorder Traversal
- Level Order Traversal or Breadth First Search or BFS
Inorder traversal visits the node in the order: Left -> Root -> Right
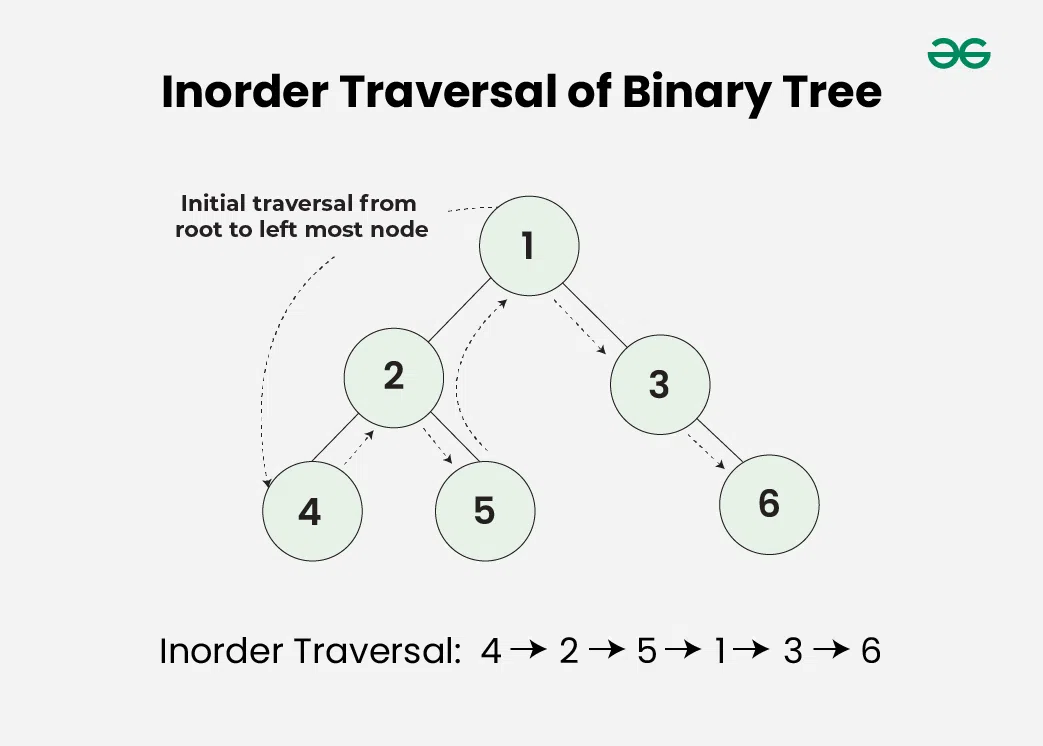
Algorithm for Inorder Traversal:
Inorder(tree)
- Traverse the left subtree, i.e., call Inorder(left->subtree)
- Visit the root.
- Traverse the right subtree, i.e., call Inorder(right->subtree)
Uses of Inorder Traversal:
- In the case of binary search trees (BST), Inorder traversal gives nodes in non-decreasing order.
- To get nodes of BST in non-increasing order, a variation of Inorder traversal where Inorder traversal is reversed can be used.
- Inorder traversal can be used to evaluate arithmetic expressions stored in expression trees.
Code Snippet for Inorder Traversal:
C++
// Given a binary tree, print its nodes in inorder
void printInorder(struct Node* node)
{
if (node == NULL)
return;
// First recur on left child
printInorder(node->left);
// Then print the data of node
cout << node->data << " ";
// Now recur on right child
printInorder(node->right);
}
// Given a binary tree, print its nodes in inorder
void printInorder(struct node* node)
{
if (node == NULL)
return;
// First recur on left child
printInorder(node->left);
// Then print the data of node
printf("%d ", node->data);
// Now recur on right child
printInorder(node->right);
}
void printInorder(Node node)
{
if (node == null)
return;
// First recur on left child
printInorder(node.left);
// Then print the data of node
System.out.print(node.key + " ");
// Now recur on right child
printInorder(node.right);
}
# A function to do inorder tree traversal
def printInorder(root):
if root:
# First recur on left child
printInorder(root.left)
# Then print the data of node
print(root.val, end=" "),
# Now recur on right child
printInorder(root.right)
// Given a binary tree, print
// its nodes in inorder
void printInorder(Node node)
{
if (node == null)
return;
// First recur on left child
printInorder(node.left);
// Then print the data of node
Console.Write(node.key + " ");
// Now recur on right child
printInorder(node.right);
}
// Given a binary tree, print its nodes in inorder
function printInorder(node) {
if (node == null)
return;
// First recur on left child */
printInorder(node.left);
// Then print the data of node
console.log(node.key + " ");
// Now recur on right child
printInorder(node.right);
}
OutputInorder traversal of binary tree is
4 2 5 1 3
Time Complexity: O(N)
Auxiliary Space: If we don’t consider the size of the stack for function calls then O(1) otherwise O(h) where h is the height of the tree.
Preorder traversal visits the node in the order: Root -> Left -> Right
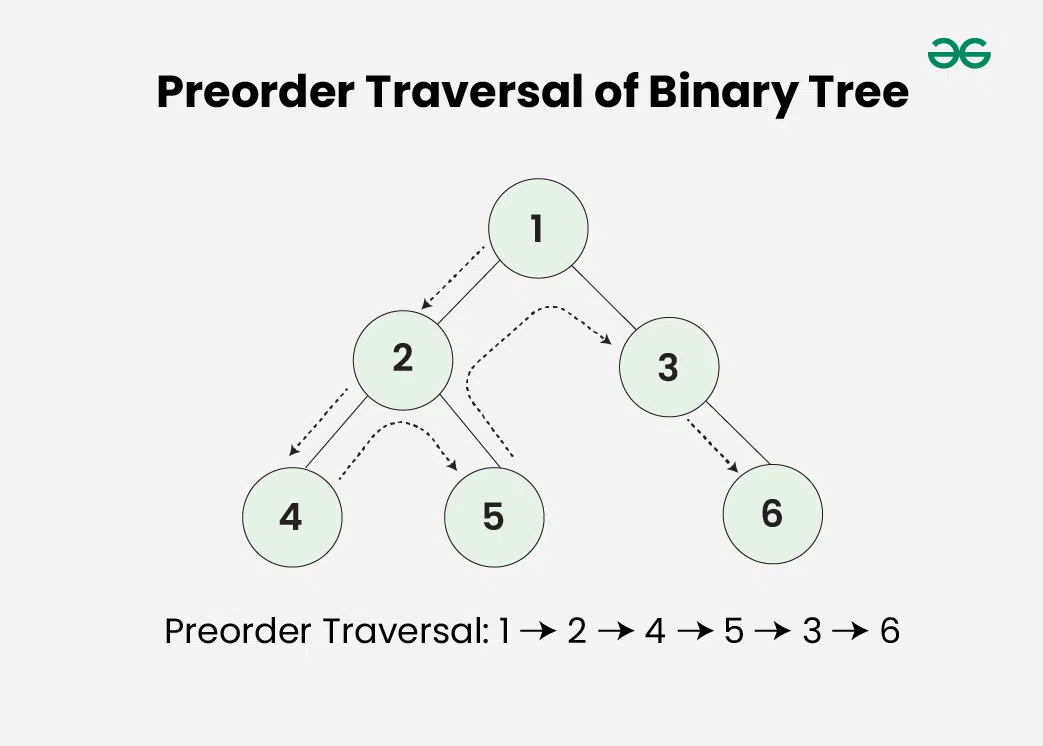
Algorithm for Preorder Traversal:
Preorder(tree)
- Visit the root.
- Traverse the left subtree, i.e., call Preorder(left->subtree)
- Traverse the right subtree, i.e., call Preorder(right->subtree)
Uses of Preorder Traversal:
- Preorder traversal is used to create a copy of the tree.
- Preorder traversal is also used to get prefix expressions on an expression tree.
Code Snippet for Preorder Traversal:
C++
// Given a binary tree, print its nodes in preorder
void printPreorder(struct Node* node)
{
if (node == NULL)
return;
// First print data of node
cout << node->data << " ";
// Then recur on left subtree
printPreorder(node->left);
// Now recur on right subtree
printPreorder(node->right);
}
// Given a binary tree, print its nodes in preorder
void printPreorder(struct node* node)
{
if (node == NULL)
return;
// First print data of node
printf("%d ", node->data);
// Then recur on left subtree
printPreorder(node->left);
// Now recur on right subtree
printPreorder(node->right);
}
// Given a binary tree, print its nodes in preorder
void printPreorder(Node node)
{
if (node == null)
return;
// First print data of node
System.out.print(node.key + " ");
// Then recur on left subtree
printPreorder(node.left);
// Now recur on right subtree
printPreorder(node.right);
}
# A function to do preorder tree traversal
def printPreorder(root):
if root:
# First print the data of node
print(root.val, end=" "),
# Then recur on left child
printPreorder(root.left)
# Finally recur on right child
printPreorder(root.right)
// Given a binary tree, print
// its nodes in preorder
void printPreorder(Node node)
{
if (node == null)
return;
// First print data of node
Console.Write(node.key + " ");
// Then recur on left subtree
printPreorder(node.left);
// Now recur on right subtree
printPreorder(node.right);
}
// Given a binary tree, print its nodes in preorder
function printPreorder(node) {
if (node == null)
return;
// First print data of node
document.write(node.key + " ");
// Then recur on left subtree
printPreorder(node.left);
// Now recur on right subtree
printPreorder(node.right);
}
OutputPreorder traversal of binary tree is
1 2 4 5 3
Time Complexity: O(N)
Auxiliary Space: If we don’t consider the size of the stack for function calls then O(1) otherwise O(h) where h is the height of the tree.
Postorder traversal visits the node in the order: Left -> Right -> Root
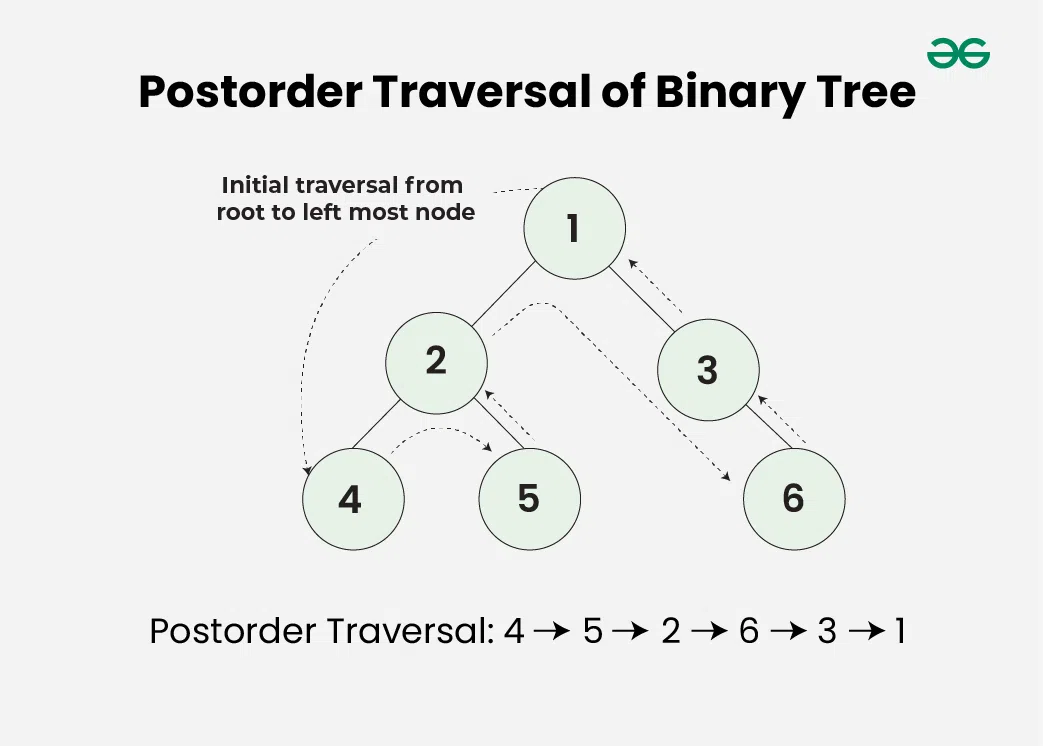
Algorithm for Postorder Traversal:
Algorithm Postorder(tree)
- Traverse the left subtree, i.e., call Postorder(left->subtree)
- Traverse the right subtree, i.e., call Postorder(right->subtree)
- Visit the root
Uses of Postorder Traversal:
- Postorder traversal is used to delete the tree. See the question for the deletion of a tree for details.
- Postorder traversal is also useful to get the postfix expression of an expression tree.
- Postorder traversal can help in garbage collection algorithms, particularly in systems where manual memory management is used.
Code Snippet for Postorder Traversal:
C++
// Given a binary tree, print its nodes according to the
// "bottom-up" postorder traversal.
void printPostorder(struct Node* node)
{
if (node == NULL)
return;
// First recur on left subtree
printPostorder(node->left);
// Then recur on right subtree
printPostorder(node->right);
// Now deal with the node
cout << node->data << " ";
}
// Given a binary tree, print its nodes according to the
// "bottom-up" postorder traversal.
void printPostorder(struct node* node)
{
if (node == NULL)
return;
// First recur on left subtree
printPostorder(node->left);
// Then recur on right subtree
printPostorder(node->right);
// Now deal with the node
printf("%d ", node->data);
}
// Given a binary tree, print its nodes according to the
// "bottom-up" postorder traversal.
void printPostorder(Node node)
{
if (node == null)
return;
// First recur on left subtree
printPostorder(node.left);
// Then recur on right subtree
printPostorder(node.right);
// Now deal with the node
System.out.print(node.key + " ");
}
# A function to do postorder tree traversal
def printPostorder(root):
if root:
# First recur on left child
printPostorder(root.left)
# The recur on right child
printPostorder(root.right)
# Now print the data of node
print(root.val, end=" "),
// Given a binary tree, print its nodes according to
// the "bottom-up" postorder traversal.
void printPostorder(Node node)
{
if (node == null)
return;
// First recur on left subtree
printPostorder(node.left);
// Then recur on right subtree
printPostorder(node.right);
// Now deal with the node
Console.Write(node.key + " ");
}
// Given a binary tree, print its nodes according
// to the "bottom-up" postorder traversal
function printPostorder(node) {
if (node == null)
return;
// First recur on left subtree
printPostorder(node.left);
// Then recur on right subtree
printPostorder(node.right);
// Now deal with the node
console.log(node.key + " ");
}
OutputPostorder traversal of binary tree is
4 5 2 3 1
Level Order Traversal visits all nodes present in the same level completely before visiting the next level.
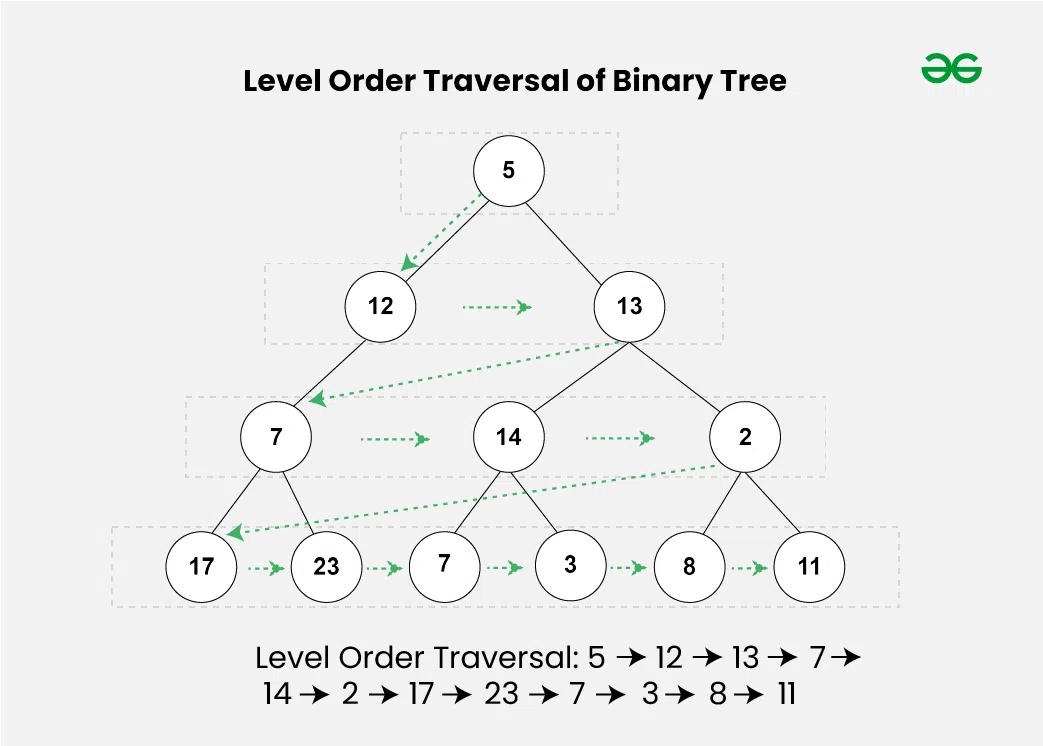
Algorithm for Level Order Traversal:
LevelOrder(tree)
- Create an empty queue Q
- Enqueue the root node of the tree to Q
- Loop while Q is not empty
- Dequeue a node from Q and visit it
- Enqueue the left child of the dequeued node if it exists
- Enqueue the right child of the dequeued node if it exists
Uses of Level Order:
Code Snippet for Level Order Traversal:
C++
// Iterative method to find height of Binary Tree
void printLevelOrder(Node* root)
{
// Base Case
if (root == NULL)
return;
// Create an empty queue for level order traversal
queue<Node*> q;
// Enqueue Root and initialize height
q.push(root);
while (q.empty() == false) {
// Print front of queue and remove it from queue
Node* node = q.front();
cout << node->data << " ";
q.pop();
// Enqueue left child
if (node->left != NULL)
q.push(node->left);
// Enqueue right child
if (node->right != NULL)
q.push(node->right);
}
}
// Given a binary tree, print its nodes in level order
// using array for implementing queue
void printLevelOrder(struct node* root)
{
int rear, front;
struct node** queue = createQueue(&front, &rear);
struct node* temp_node = root;
while (temp_node) {
printf("%d ", temp_node->data);
// Enqueue left child
if (temp_node->left)
enQueue(queue, &rear, temp_node->left);
// Enqueue right child
if (temp_node->right)
enQueue(queue, &rear, temp_node->right);
// Dequeue node and make it temp_node
temp_node = deQueue(queue, &front);
}
}
// Given a binary tree. Print
// its nodes in level order
// using array for implementing queue
void printLevelOrder()
{
Queue<Node> queue = new LinkedList<Node>();
queue.add(root);
while (!queue.isEmpty()) {
// poll() removes the present head.
Node tempNode = queue.poll();
System.out.print(tempNode.data + " ");
// Enqueue left child
if (tempNode.left != null) {
queue.add(tempNode.left);
}
// Enqueue right child
if (tempNode.right != null) {
queue.add(tempNode.right);
}
}
}
# Iterative Method to print the
# height of a binary tree
def printLevelOrder(root):
# Base Case
if root is None:
return
# Create an empty queue
# for level order traversal
queue = []
# Enqueue Root and initialize height
queue.append(root)
while(len(queue) > 0):
# Print front of queue and
# remove it from queue
print(queue[0].data, end=" ")
node = queue.pop(0)
# Enqueue left child
if node.left is not None:
queue.append(node.left)
# Enqueue right child
if node.right is not None:
queue.append(node.right)
// Given a binary tree. Print
// its nodes in level order using
// array for implementing queue
void printLevelOrder()
{
Queue<Node> queue = new Queue<Node>();
queue.Enqueue(root);
while (queue.Count != 0) {
Node tempNode = queue.Dequeue();
Console.Write(tempNode.data + " ");
// Enqueue left child
if (tempNode.left != null) {
queue.Enqueue(tempNode.left);
}
// Enqueue right child
if (tempNode.right != null) {
queue.Enqueue(tempNode.right);
}
}
}
// Function to perform level order traversal of a binary tree
function printLevelOrder(root) {
// Create a deque to store nodes for traversal
const queue = new Deque();
// Add the root node to the queue
queue.enqueue(root);
// Continue traversal until the queue is empty
while (!queue.isEmpty()) {
// Remove and get the first node from the queue
const tempNode = queue.dequeue();
// Print the data of the current node
console.log(tempNode.data + " ");
// Enqueue the left child if it exists
if (tempNode.left !== null) {
queue.enqueue(tempNode.left);
}
// Enqueue the right child if it exists
if (tempNode.right !== null) {
queue.enqueue(tempNode.right);
}
}
}
Other Tree Traversals:
- Boundary Traversal
- Diagonal Traversal
Boundary Traversal of a Tree includes:
- left boundary (nodes on left excluding leaf nodes)
- leaves (consist of only the leaf nodes)
- right boundary (nodes on right excluding leaf nodes)
Algorithm for Boundary Traversal:
BoundaryTraversal(tree)
- If root is not null:
- Print root’s data
- PrintLeftBoundary(root->left) // Print the left boundary nodes
- PrintLeafNodes(root->left) // Print the leaf nodes of left subtree
- PrintLeafNodes(root->right) // Print the leaf nodes of right subtree
- PrintRightBoundary(root->right) // Print the right boundary nodes
Uses of Boundary Traversal:
- Boundary traversal helps visualize the outer structure of a binary tree, providing insights into its shape and boundaries.
- Boundary traversal provides a way to access and modify these nodes, enabling operations such as pruning or repositioning of boundary nodes.
In the Diagonal Traversal of a Tree, all the nodes in a single diagonal will be printed one by one.
Algorithm for Diagonal Traversal:
DiagonalTraversal(tree):
- If root is not null:
- Create an empty map
- DiagonalTraversalUtil(root, 0, M) // Call helper function with initial diagonal level 0
- For each key-value pair (diagonalLevel, nodes) in M:
- For each node in nodes:
- Print node’s data
DiagonalTraversalUtil(node, diagonalLevel, M):
- If node is null:
- Return
- If diagonalLevel is not present in M:
- Create a new list in M for diagonalLevel
- Append node’s data to the list at M[diagonalLevel]
- DiagonalTraversalUtil(node->left, diagonalLevel + 1, M) // Traverse left child with increased diagonal level
- DiagonalTraversalUtil(node->right, diagonalLevel, M) // Traverse right child with same diagonal level
Uses of Diagonal Traversal:
- Diagonal traversal helps in visualizing the hierarchical structure of binary trees, particularly in tree-based data structures like binary search trees (BSTs) and heap trees.
- Diagonal traversal can be utilized to calculate path sums along diagonals in a binary tree.
Frequently Asked Questions (FAQs) on Tree Traversal Techniques:
1. What are tree traversal techniques?
Tree traversal techniques are methods used to visit and process all nodes in a tree data structure. They allow you to access each node exactly once in a systematic manner.
2. What are the common types of tree traversal?
The common types of tree traversal are: Inorder traversal, Preorder traversal, Postorder traversal, Level order traversal (Breadth-First Search)
3. What is Inorder traversal?
Inorder traversal is a depth-first traversal method where nodes are visited in the order: left subtree, current node, right subtree.
4. What is preorder traversal?
Preorder traversal is a depth-first traversal method where nodes are visited in the order: current node, left subtree, right subtree.
5. What is postorder traversal?
Postorder traversal is a depth-first traversal method where nodes are visited in the order: left subtree, right subtree, current node.
6. What is level order traversal?
Level order traversal, also known as Breadth-First Search (BFS), visits nodes level by level, starting from the root and moving to the next level before traversing deeper.
7. When should I use each traversal technique?
Inorder traversal is often used for binary search trees to get nodes in sorted order.
Preorder traversal is useful for creating a copy of the tree.
Postorder traversal is commonly used in expression trees to evaluate expressions.
Level order traversal is helpful for finding the shortest path between nodes.
8. How do I implement tree traversal algorithms?
Tree traversal algorithms can be implemented recursively or iteratively, depending on the specific requirements and programming language being used.
9. Can tree traversal algorithms be applied to other tree-like structures?
Yes, tree traversal algorithms can be adapted to traverse other tree-like structures such as binary heaps, n-ary trees, and graphs represented as trees.
10. Are there any performance considerations when choosing a traversal technique?
Performance considerations depend on factors such as the size and shape of the tree, available memory, and specific operations being performed during traversal. In general, the choice of traversal technique may affect the efficiency of certain operations, so it’s important to choose the most suitable method for your specific use case.
Some other important Tutorials:
Share your thoughts in the comments
Please Login to comment...