Mean in Mathematics is the measure of central tendency and is mostly used in Statistics. Mean is the easiest of all the measures. Data is of two types, Grouped data and ungrouped data. The method of finding the mean is also different depending on the type of data. Mean is generally the average of a given set of numbers or data. It is one of the most important measures of the central tendency of distributed data.
In statistics, the mean is the average of a data set. It is calculated by adding all the numbers in the data set and dividing by the number of values in the set. The mean is also known as the average. It is sensitive to skewed data and extreme values. For example, when the data are skewed, it can miss the mark.
In this article, we’ll explore all the things you need to know about What is Mean, Mean Definition, Mean Formula, Mean Examples, and others in detail.
Central Tendency in Statistics
In statistics, three measures are defined as central tendencies that are, Mean, Median, and Mode, where mean provides the average value of the dataset, median provides the central value of the dataset, and the most frequent value in the dataset is mode.
Calculation of central tendency such as mean, median, and mode is very useful in a lot of fields of study such as Data Science, Statistics, and Machine Learning.
What is Mean in Statistics?
Mean in Statistics means we are dealing with mean in the subject of statistics as mean is a very general term. If we want to find the mean of a set of given values (ungrouped data), just add the values and divide the sum by the number of values.
Mean is the central tendency of the distributed data, which refers to the average value of the given set of data. The mean corresponds to the single value from the distributed data and represents an appropriate value that can give us insights into the data. In statistics mean is one of the most basic methods for the analysis of data.
For example, if we want to calculate the average salary of employees present in a company can be calculated by using the mean by dividing the sum of all employee salaries and the number of employees or we want to calculate the average revenue per employee this can be calculated again by the division of total revenue by the number of employees.
Mean Definition
Mean is defined as the average of the given set of values and is used to measure of the central tendency. Central tendency is the measure that acknowledges the set of data or the distribution from a value. Therefore, it can be said that mean can describe the entire data. In statistics, the mean can be obtained by dividing the sum of observations by the total number of observations.
Mean Symbol
Mean is denoted as a bar on x or 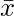 . Let’s say the dataset given is X = {x1, x2, x3, . . ., xn} The mean of this dataset is denoted as
. Let’s say the dataset given is X = {x1, x2, x3, . . ., xn} The mean of this dataset is denoted as 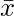 and is given by:
and is given by:

Mean Application
There are many uses and examples of mean in real life. Following are some of the real-life examples of mean:
- The average (mean) marks obtained by the students in a class.
- A cricketer’s average is also an example of a mean.
- The average salary package is also used for the marketing of the colleges and their placement cell.
Mean formula in statistics is defined as the sum of all observations in the given dataset divided by the total number of observations. The image added below shows the mean formula of given observation.

We use mean formula to easily calculate the mean of given data set for example,
Example: Calculate the mean of the first 10 natural numbers.
Solution:
First 10 natural numbers = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Sum of first 10 natural numbers = (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10)
Mean = Sum of 10 natural numbers/10
⇒ Mean = (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10)/10
⇒ Mean = 55/10
⇒ Mean = 5.5
How to Find Mean?
To find the mean value, we use the mean formula, which calculates the average of the given data. It is calculated by dividing the sum of all observed data values by the number of observed values. The mean formula is given by
Mean = (Sum of observed values in data)/(Total number of observed values in data)
There are two steps involved in the calculation of the mean:
Step 1: Calculate the sum of observed values in the data.
Step 2: Divide the sum of observed values into the number of observed values in the data.
Based on the type of dataset given, we can find out the mean using different methods. Let’s take a look at the different cases to find the mean:
Case 1: If there are ‘n’ number of items in a list. The data is {x1, x2, x3, … xn}. The Mean is calculated using the formula:


Case 2: Let’s assume there are n number of items in a set i.e., {x1, x2, x3, … xn}, and the frequency of each item is given as {f1, f2, f3, . . ., fn}. Then, the mean is calculated using the formula:


Case 3: When items of the set are given in the form of a range, for example, 1-10, 10-20, etc. To find the mean first we need to calculate the class mark for each class interval and then, the mean is calculated using the given formula:

Mean of Ungrouped Data
The mean of ungrouped data is the sum of all the observations divided by the total number of observations. Ungrouped data is known as raw data, where the dataset simply contains all the data in no particular manner. Following are the steps that are to be followed to find the mean of ungrouped data:
- Note down the entire dataset for which the mean is to be calculated.
- Now, apply any of the two formulas added below based on the observation of data.
Mean Formula For Ungrouped Data
The mean formula for ungrouped data is added below,


The mean formula for ungrouped data added above is used to find mean of ungrouped data, for example,
Example: Calculate the mean for the following set of data 2, 6, 7, 9, 15, 11, 13, 12.
Solution:
Given,
- Observed values 2, 6, 7, 9, 15, 11, 13, 12
- Total number of observed values = 8
Using Mean Formula for Grouped Data
Mean = (Sum of observed values in data) / (Total number of observed values in data)
Sum of observed values = 2 + 6 + 7 + 9 + 15 + 11 + 13 + 12 = 75
Total number of observed values = 8
Mean = 75/8
⇒ Mean = 9.375
Therefore, mean for the given observed values = 9.375
Types of Mean
In statistics, there are four types of mean, and they are weighted mean, Arithmetic Mean (AM), Geometric Mean (GM), and Harmonic Mean (HM). When not specified, the mean is generally referred to as the arithmetic mean. Let’s take a look into all the types of mean:
Arithmetic Mean
The arithmetic mean is calculated for a given set of data by calculating the ratio of the sum of all observed values to the total number of observed values. When the specification of the mean is not given, it is presumed that the mean is an arithmetic mean. The general formula for arithmetic mean is given as:
Arithmetic Mean = (Sum of observed values)÷(Number of observed values in data)

Where,
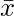 = Arithmetic mean
= Arithmetic mean- Fi = Frequency of each data
- N = Number of frequencies.
Geometric Mean
The geometric mean is calculated for a set of n values by calculating the nth root of the product of all n observed values. It is defined as the nth root of the product of n numbers in the dataset. The formula for the geometric mean is given as:
Geometric Mean = nth root of (x1 × x2 × x3 × x4 …. n values)
![Rendered by QuickLaTeX.com \bold{G.M. = \sqrt[n]{x_1\times x_2\times x_3\times \ldots \times x_n}}](https://quicklatex.com/cache3/04/ql_2af31e9a5f3ad01f9fbd73586f104f04_l3.png)
Harmonic Mean
The harmonic mean is calculated by dividing the number of values in the observed set by the sum of reciprocals of each observed data value. Therefore, the harmonic mean can also be called the reciprocal of the arithmetic mean. The formula for harmonic mean is given as:
Harmonic Mean = (Number of Observed Values) / (1/n1 + 1/n2 + 1/n3 + . . .)

Weighted Mean
Weighted Mean is calculated in certain cases of the dataset when the given set of data has some values more important than the other. In the dataset, a weight ‘wi‘ is connected to each data ‘xi‘, and the general formula for weighted mean is given as:

Where,
- xi is ith observations, and
- wi is the Weight of ith observations.
Mean of Grouped Data
Grouped data is the set of data that is obtained by forming individual observations of variables into groups. Grouped data is divided into groups. A frequency distribution table is required for the grouped data, which helps showcase the frequencies of the given data. The mean of grouped data can be obtained using three methods. The methods are:
- Direct Method
- Assumed Mean Method
- Step Deviation Method
Calculating Mean Using Direct Method
The direct method is the simplest method to find the mean of grouped data. The mean of grouped data using the direct method can be calculated using the following steps:
- Four columns are created in the table. The columns are Class interval, class marks (xi), frequencies (fi), the product of frequencies, and class marks (fi xi).
- Now, calculate the mean of grouped data using the formula
Mean Formula For Grouped Data (Using Direct Method)
The mean formula for grouped data using direct method is added below,

Example: Calculate the mean height for the following data using the direct method.
Height (in inches)
| 60 – 62
| 62 – 64
| 64 – 66
| 66 – 68
| 68 – 70
| 70 – 72
|
|---|
Frequency
| 3
| 6
| 9
| 12
| 8
| 2
|
|---|
Solution:
As, 
Height (in inches)
| Frequency(fi)
| Midpoint (xi)
| fi × xi
|
|---|
60 – 62
| 3
| 61
| 183
|
62 – 64
| 6
| 63
| 378
|
64 – 66
| 9
| 65
| 585
|
66 – 68
| 12
| 67
| 804
|
68 – 70
| 8
| 69
| 552
|
70 – 72
| 2
| 71
| 142
|
| | ∑fi = 40
|
| ∑fi xi = 2644
|
⇒ Mean = 2644/40 = 66.1
Thus, mean height is 66.1 inches.
Calculating Mean Using Assumed Mean Method
When the calculation of the mean for grouped data using the direct method becomes very tedious, then the mean can be calculated using the assumed mean method. To find the mean using the assumed mean method the following steps are needed:
- Five columns are created in the table i.e., class interval, class marks (xi), corresponding deviations (di = xi – A) where A is the central value from class marks as assumed mean, frequencies (fi), and product of fi and di.
- Now, the mean value can be calculated for the given data using the following formula.
Mean Formula For Grouped Data (Using Assumed Mean Method)
The mean formula for grouped data using assumed mean method is added below,

Example: Calculate the mean of the following data using the Assumed Mean Method.
Weight (in kg)
| 40 – 44
| 44 – 48
| 48 – 52
| 52 – 56
| 56 – 60
| 60 – 64
|
|---|
Frequency
| 2
| 3
| 5
| 7
| 2
| 1
|
|---|
Solution:
Let us assume the value of mean be A = 53,
and the required table for the given data is as follows for A = 53:
Weight (in kg)
| Frequency(fi)
| Midpoint (xi)
| Deviation (di = xi – A)
|
|---|
40 – 44
| 2
| 42
| -11
|
44 – 48
| 3
| 46
| -7
|
48 – 52
| 5
| 50
| -3
|
52 – 56
| 7
| 54
| 1
|
56 – 60
| 2
| 58
| 5
|
60 – 64
| 1
| 62
| 9
|
Add one more column to the table which give product of fi and di :
Weight (in kg)
| Frequency(fi)
| Midpoint (xi)
| Deviation (di = xi – A)
| fi × di
|
|---|
40 – 44
| 2
| 42
| -11
| -22
|
44 – 48
| 3
| 46
| -7
| -21
|
48 – 52
| 5
| 50
| -3
| -15
|
52 – 56
| 7
| 54
| 1
| 7
|
56 – 60
| 2
| 58
| 5
| 10
|
60 – 64
| 1
| 62
| 9
| 9
|
| ∑fi = 20
|
|
| ∑fi di = -32
|
Thus, Mean = 53 + (-32)/20 = 53 – 1.6 = 51.4
Thus, mean weight of the given data using assumed mean method is 51.4 Kg.
Calculating Mean Using Step Deviation Method
Step deviation method is also famously known as the scale method or shift of origin method. When finding the mean of grouped data becomes tedious, using step deviation method can be used. Following are the steps that should be followed while using the step deviation method:
- Five columns are created in the table. They are class interval, class marks (xi, here the central value is A), deviations (di), ui = di/h (h is class width), and product of fi and UIi.
- Now, the mean of the data can be calculated using the following formula
Mean Formula For Grouped Data (Using Step Deviation Method)
The mean formula for grouped data using step deviation mean method is added below,

Example: Calculate the mean of the following data using the Step Deviation method.
Age(in year)
| 20-24
| 24-28
| 28-32
| 32-36
| 36-40
| 40-44
| 44-48
|
|---|
Frequency
| 3
| 6
| 8
| 5
| 5
| 2
| 1
|
|---|
Solution:
Range of the data is 20 to 48, for assumption of mean, lets take average of the range values,
Assumed mean = (20 + 48) /2 = 68/2 = 34
Let’s A = 34 be the assumed mean of the data,
Now, using assumed mean value, let’s create the table for step deviation as follows:
Age (in years)
| Frequency(fi)
| Class Mark(xi)
| Deviation(di = xi – A)
| Step Deviation (ui = di/h)
| fi × ui
|
|---|
20 – 24
| 3
| 22
| -12
| -3
| -9
|
24 – 28
| 6
| 26
| -8
| -2
| -12
|
28 – 32
| 8
| 30
| -4
| -1
| -8
|
32 – 36
| 5
| 34
| 0
| 0
| 0
|
36 – 40
| 5
| 38
| 4
| 1
| 5
|
40 – 44
| 2
| 42
| 8
| 2
| 4
|
44 – 48
| 1
| 46
| 12
| 3
| 3
|
| | ∑fi = 20 | | | | ∑fi ui =- 17 |
Thus, Mean = 34 + 4 × (-17)/20 = 34 + 4 × (-0.85) = 34 – 3.4 = 30.6
Thus, mean age of data using step deviation method is 30.6
Arithmetic Mean vs. Geometric Mean
There are key differences between Arithmetic Mean and Geometric Mean, which can be listed as follows:
Arithmetic Mean
| Geometric Mean
|
|---|
| Sum of all values divided by the number of values | nth root of the product of all values |
| Suitable for symmetrical data with no extreme values | Suitable for data with positive values and extreme values |
| Sensitive to extreme values | Not sensitive to extreme values |
| Used for measuring the central tendency of data | Used for measuring the average growth rate |
| Can be used for both discrete and continuous data | Usually used for continuous data |
| Additive in nature | Multiplicative in nature |
| Denoted by “x̄” or “AM” | Denoted by “G” or “GM” |
Example 1: Calculate the mean of the first 5 even natural numbers.
Solution:
Given,
- Observed first 5 even natural numbers 2, 4, 6, 8, 10
- Total number of observed values = 5
Using Mean Formula
Mean = (Sum of observed values in data)/(Total number of observed values in data)
⇒ Sum of observed values = 2 + 4 + 6 + 8 + 10 = 30
Total number of observed values = 5
⇒ Mean = 30/5
⇒ Mean = 6
Therefore, mean for first 5 even numbers = 6
Example 2: Calculate the mean of the first 10 natural odd numbers.
Solution:
Given,
- Observed first 5 odd natural numbers 1, 3, 5, 7, 9.
- Total number of observed values = 5
Using Mean Formula
Mean = (Sum of observed values in data)/(Total number of observed values in data)
Sum of observed values = 1 + 3 + 5 + 7 + 9 = 25
Total number of observed values = 5
⇒ Mean = 25 / 5
⇒ Mean = 5
Therefore, mean for first 5 odd numbers = 5
Example 3: Calculate missing values from the observed set 2, 6, 7, x, whose mean is 6.
Solution:
Given,
- Observed values 2, 6, 7, x
- Number of observed values = 4
- Mean = 6
Using Mean Formula
Mean = (Sum of observed values in data)/(Total number of observed values in data)
⇒ Sum of observed values = 2 + 6 + 7 + x = 15 + x
Total number of observed values = 4
⇒ 6 = (15 + x)/4
⇒ 6 × 4 = 15 + x
⇒ x = 9
Therefore, missing value from the set is 9
Example 4: There are 20 students in class 10. The marks obtained by the students in mathematics (out of 100) are given below. Calculate the mean of the marks.
| Marks Obtained | Number of students |
|---|
100
| 1
|
92
| 3
|
80
| 5
|
75
| 10
|
70
| 1
|
Solution:
Given,
- Total number of students in class 10 = 20
- x1 = 100, x2 = 92, x3 = 80, x4 = 75, x5 = 70
- f1 = 1, f2 = 3, f3 = 5, f4 = 10, f5 = 1
Using Mean Formula

⇒ x̄ = {(100 × 1) + (92 × 3) + (80 × 5) + (75 × 10) + (70 × 1)}/20
⇒ x̄ = (100 + 276 + 400 + 750 + 70)/20
⇒ x̄ = 1596/20 = 79.8 marks
Example 5: Calculate the mean of the following dataset.
Height (in inches)
| 60 – 62
| 62 – 64
| 64 – 66
| 66 – 68
| 68 – 70
| 70 – 72
| 72 – 74
| 74 – 76
|
|---|
Frequency
| 2
| 3
| 4
| 6
| 5
| 3
| 1
| 1
|
|---|
Solution:
Range of data is 60 to 76, for assumption of mean, lets take average of the range values,
Assumed Mean = (60 + 76) /2 = 136/2 = 68
Now, Let’s A = 68 be assumed mean of the data,
Now, using assumed mean value, let’s create the table for step deviation as follows:
Height (in inches)
| Frequency(fi)
| Class Mark (xi)
| Deviation (di)
| Step Deviation (ui)
| fi × ui
|
|---|
60 – 62
| 2
| 61
| -7
| -3.5
| -7
|
62 – 64
| 3
| 63
| -5
| -2.5
| -7.5
|
64 – 66
| 4
| 65
| -3
| -1.5
| -6
|
66 – 68
| 6
| 67
| -1
| -0.5
| -3
|
68 – 70
| 5
| 69
| 1
| 0.5
| 2.5
|
70 – 72
| 3
| 71
| 3
| 1.5
| 4.5
|
72 – 74
| 1
| 73
| 5
| 2.5
| 2.5
|
74 – 76
| 1
| 75
| 7
| 3.5
| 3.5
|
| | ∑f = 25 | | | | ∑fiui = -10.5 |
Thus, Mean = 68 + 2 × (-10.5)/25
⇒ Mean = 68 + 2 × (-0.42)
⇒ Mean = 68 – 0.84 = 67.16
Thus, mean height of data using step deviation method is 67.16 inches.
Practice Questions on Mean
Q1: Find the Mean temperature of a week given that the temperatures from Monday to Sunday are 21℃, 23℃, 22.5℃, 21.6℃, 22.3℃, 24℃, 20.5℃.
Q2: Find the Mean height of students if the given heights are 150 cm, 152 cm, 155 cm, 160 cm, 148 cm.
Q3: Find the Mean of the given dataset
Marks
| Number of Students
|
|---|
|
0-10
|
3
|
|
10-20
|
5
|
|
20-30
|
9
|
|
30-40
|
8
|
|
40-50
|
5
|
Mean – FAQs
What is Mean in Statistics?
Mean in statistics is one of the important measures of central tendency, it is defined as the average of the set of values given.
What is Mean Formula?
There area different mean formulas based on the type of data present.
For ungrouped data,
Mean = (Sum of Observations) ÷ (Total number of observations)
For grouped data,
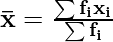
What are Different Types of Mean?
There are four different types of mean, that are:
- Arithmetic Mean
- Geometric Mean
- Harmonic Mean
- Weighted Mean
What are Applications of Mean in Real-Life?
There are many applications of mean in real-life. For example, in schools, the mean of marks in subjects are taken by teachers, the HR managers often find out the mean of salaries of employees, etc.
What is Mean Formula for ‘n’ Number of Observations?
Mean formula for ‘n’ number of observations is:
Mean = (Sum of n Observations)÷(Number of Observations)

What is Mean Formula for Grouped Data?
Mean formula to find the mean of a grouped set of data is,
x̄ = Σfixi/Σfi
What is Mean Formula for Ungrouped Data?
Mean formula to find the mean for an ungrouped set of data is,
Mean = (Sum of Data Values) / (Number of Data Values)
What is Mean of First 10 Natural Numbers?
First 10 natural numbers are: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Sum of first 10 natural numbers = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55; Mean = 55/10 = 5.5
How do you Calculate Mean with Examples?
Mean of the data set is calculated by using the mean formula as,
Mean = (Sum of Observation)/(Number of Observation)
Example: Mean of 1, 2, and 3 is (1 + 2 + 3) / 3 = 6 / 3 = 2
How to Find Average?
Average is the other name of Arithmetic Mean, and it is calculated by adding all the given numbers and then dividing the sum by the count of the number.
Find Mean of First 5 Composite Numbers?
First five composite numbers are 4, 6, 8, 9, 10 mean of these numbers (4 + 6 + 8 + 9 + 10)/5 = 37/5 = 7. 4
What is Mean of First 5 Even Natural Numbers?
First five even natural numbers are 2, 4, 6, 8, 10 mean of these numbers (2 + 4 + 6 + 8 + 10)/5 = 30/5 = 6
What is Relationship between Mean, Median and Mode?
Relation between Mean, Median and Mode is Mode = 3(median) – 2(mean)
How is Mean Represented?
Mean is represented by Greek Symbol, (μ)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...