Bit stands for binary digit. A bit is the basic unit of information and can only have one of two possible values that is 0 or 1.
In our world, we usually with numbers using the decimal base. In other words. we use the digit 0 to 9 However, there are other number representations that can be quite useful such as the binary number systems.

Introduction to Bitwise Algorithms – Data Structures and Algorithms Tutorial
Unlike humans, computers have no concepts of words and numbers. They receive data encoded at the lowest level as a series of zeros and ones (0 and 1). These are called bits, and they are the basis for all the commands they receive. We’ll begin by learning about bits and then explore a few algorithms for manipulating bits. We’ll then explore a few algorithms for manipulating bits. The tutorial is meant to be an introduction to bit algorithms for programmers.
Basics of Bit manipulation (Bitwise Operators)
An algorithmic operation known as bit manipulation involves the manipulation of bits at the bit level (bitwise). Bit manipulation is all about these bitwise operations. They improve the efficiency of programs by being primitive, fast actions.
The computer uses this bit manipulation to perform operations like addition, subtraction, multiplication, and division are all done at the bit level. This operation is performed in the arithmetic logic unit (ALU) which is a part of a computer’s CPU. Inside the ALU, all such mathematical operations are performed.
There are different bitwise operations used in bit manipulation. These bit operations operate on the individual bits of the bit patterns. Bit operations are fast and can be used in optimizing time complexity. Some common bit operators are:
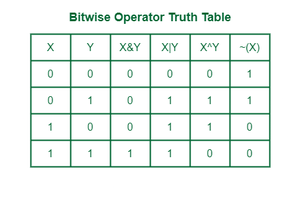
Bitwise Operator Truth Table
1. Bitwise AND Operator (&)
The bitwise AND operator is denoted using a single ampersand symbol, i.e. &. The & operator takes two equal-length bit patterns as parameters. The two-bit integers are compared. If the bits in the compared positions of the bit patterns are 1, then the resulting bit is 1. If not, it is 0.
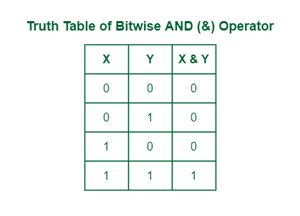
Truth table of AND operator
Example:
Take two bit values X and Y, where X = 7= (111)2 and Y = 4 = (100)2 . Take Bitwise and of both X & y

Bitwise ANDof (7 & 4)
Implementation of AND operator:
C++
#include <bits/stdc++.h>
using namespace std;
int main()
{
int a = 7, b = 4;
int result = a & b;
cout << result << endl;
return 0;
}
|
Java
import java.io.*;
class GFG {
public static void main (String[] args) {
int a = 7, b = 4;
int result = a & b;
System.out.println(result);
}
}
|
Python3
a = 7
b = 4
result = a & b
print(result)
|
C#
using System;
public class GFG{
static public void Main (){
int a = 7, b = 4;
int result = a & b;
Console.WriteLine(result);
}
}
|
Javascript
let a = 7, b = 4;
let result = a & b;
console.log(result);
|
Time Complexity: O(1)
Auxiliary Space: O(1)
2. Bitwise OR Operator (|)
The | Operator takes two equivalent length bit designs as boundaries; if the two bits in the looked-at position are 0, the next bit is zero. If not, it is 1.
.png)
Example:
Take two bit values X and Y, where X = 7= (111)2 and Y = 4 = (100)2 . Take Bitwise OR of both X, y

Bitwise OR of (7 | 4)
Explanation: On the basis of truth table of bitwise OR operator we can conclude that the result of
1 | 1 = 1
1 | 0 = 1
0 | 1 = 1
0 | 0 = 0
We used the similar concept of bitwise operator that are show in the image.
Implementation of OR operator:
C++
#include <bits/stdc++.h>
using namespace std;
int main()
{
int a = 12, b = 25;
int result = a | b;
cout << result;
return 0;
}
|
Java
import java.io.*;
class GFG {
public static void main(String[] args)
{
int a = 12, b = 25;
int result = a | b;
System.out.println(result);
}
}
|
Python3
a = 12
b = 25
result = a | b
print(result)
|
C#
using System;
public class GFG{
static public void Main (){
int a = 12, b = 25;
int result = a | b;
Console.WriteLine(result);
}
}
|
Javascript
let a = 12, b = 25;
let result = a | b;
document.write(result);
|
Time Complexity: O(1)
Auxiliary Space: O(1)
3. Bitwise XOR Operator (^)
The ^ operator (also known as the XOR operator) stands for Exclusive Or. Here, if bits in the compared position do not match their resulting bit is 1. i.e, The result of the bitwise XOR operator is 1 if the corresponding bits of two operands are opposite, otherwise 0.
.png)
Example:
Take two bit values X and Y, where X = 7= (111)2 and Y = 4 = (100)2 . Take Bitwise and of both X & y

Bitwise OR of (7 ^ 4)
Explanation: On the basis of truth table of bitwise XOR operator we can conclude that the result of
1 ^ 1 = 0
1 ^ 0 = 1
0 ^ 1 = 1
0 ^ 0 = 0
We used the similar concept of bitwise operator that are show in the image.
Implementation of XOR operator:
C++
#include <iostream>
using namespace std;
int main()
{
int a = 12, b = 25;
cout << (a ^ b);
return 0;
}
|
Java
import java.io.*;
class GFG {
public static void main(String[] args)
{
int a = 12, b = 25;
int result = a ^ b;
System.out.println(result);
}
}
|
Python3
a = 12
b = 25
result = a ^ b
print(result)
|
C#
using System;
public class GFG {
static public void Main()
{
int a = 12, b = 25;
int result = a ^ b;
Console.WriteLine(result);
}
}
|
Javascript
let a = 12;
let b = 25;
console.log((a ^ b));
|
Time Complexity: O(1)
Auxiliary Space: O(1)
4. Bitwise NOT Operator (!~)
All the above three bitwise operators are binary operators (i.e, requiring two operands in order to operate). Unlike other bitwise operators, this one requires only one operand to operate.
The bitwise Not Operator takes a single value and returns its one’s complement. The one’s complement of a binary number is obtained by toggling all bits in it, i.e, transforming the 0 bit to 1 and the 1 bit to 0.

Truth Table of Bitwise Operator NOT
Example:
Take two bit values X and Y, where X = 5= (101)2 . Take Bitwise NOT of X.

Explanation: On the basis of truth table of bitwise NOT operator we can conclude that the result of
~1 = 0
~0 = 1
We used the similar concept of bitwise operator that are show in the image.
Implementation of NOT operator:
C++
#include <iostream>
using namespace std;
int main()
{
int a = 0;
cout << "Value of a without using NOT operator: " << a;
cout << "\nInverting using NOT operator (with sign bit): " << (~a);
cout << "\nInverting using NOT operator (without sign bit): " << (!a);
return 0;
}
|
Java
import java.io.*;
class GFG {
public static void main(String[] args)
{
int a = 0;
System.out.println(
"Value of a without using NOT operator: " + a);
System.out.println(
"Inverting using NOT operator (with sign bit): "
+ (~a));
if (a != 1)
System.out.println(
"Inverting using NOT operator (without sign bit): 1");
else
System.out.println(
"Inverting using NOT operator (without sign bit): 0");
}
}
|
Python3
a = 0
print("Value of a without using NOT operator: " , a)
print("Inverting using NOT operator (with sign bit): " , (~a))
print("Inverting using NOT operator (without sign bit): " , int(not(a)))
|
C#
using System;
public class GFG {
static public void Main()
{
int a = 0;
Console.WriteLine(
"Value of a without using NOT operator: " + a);
Console.WriteLine(
"Inverting using NOT operator (with sign bit): "
+ (~a));
if (a != 1)
Console.WriteLine(
"Inverting using NOT operator (without sign bit): 1");
else
Console.WriteLine(
"Inverting using NOT operator (without sign bit): 0");
}
}
|
Javascript
let a =0;
document.write("Value of a without using NOT operator: " + a);
document.write( "Inverting using NOT operator (with sign bit): " + (~a));
if(!a)
document.write( "Inverting using NOT operator (without sign bit): 1" );
else
document.write( "Inverting using NOT operator (without sign bit): 0" );
|
Output
Value of a without using NOT operator: 0
Inverting using NOT operator (with sign bit): -1
Inverting using NOT operator (without sign bit): 1
Time Complexity: O(1)
Auxiliary Space: O(1)
5. Left-Shift (<<)
The left shift operator is denoted by the double left arrow key (<<). The general syntax for left shift is shift-expression << k. The left-shift operator causes the bits in shift expression to be shifted to the left by the number of positions specified by k. The bit positions that the shift operation has vacated are zero-filled.
Note: Every time we shift a number towards the left by 1 bit it multiply that number by 2.

Logical left Shift
Example:
Input: Left shift of 5 by 1.
Binary representation of 5 = 00101 and Left shift of 001012 by 1 (i.e, 00101 << 1)

Left shift of 5 by 1
Output: 10
Explanation: All bit of 5 will be shifted by 1 to left side and this result in 010102, Which is equivalent to 10
Input: Left shift of 5 by 2.
Binary representation of 5 = 00101 and Left shift of 001012 by 1 (i.e, 00101 << 2)

Left shift of 5 by 2
Output: 20
Explanation: All bit of 5 will be shifted by 1 to left side and this result in 101002, Which is equivalent to 20
Input: Left shift of 5 by 3.
Binary representation of 5 = 00101 and Left shift of 001012 by 1 (i.e, 00101 << 3)

Left shift of 5 by 3
Output: 40
Explanation: All bit of 5 will be shifted by 1 to left side and this result in 010002, Which is equivalent to 40
Implementation of Left shift operator:
C++
#include <bits/stdc++.h>
using namespace std;
int main()
{
unsigned int num1 = 1024;
bitset<32> bt1(num1);
cout << bt1 << endl;
unsigned int num2 = num1 << 1;
bitset<32> bt2(num2);
cout << bt2 << endl;
unsigned int num3 = num1 << 2;
bitset<16> bitset13{ num3 };
cout << bitset13 << endl;
}
|
Java
import java.io.*;
class GFG {
public static void main(String[] args)
{
int num1 = 1024;
String bt1 = Integer.toBinaryString(num1);
bt1 = String.format("%32s", bt1).replace(' ', '0');
System.out.println(bt1);
int num2 = num1 << 1;
String bt2 = Integer.toBinaryString(num2);
bt2 = String.format("%32s", bt2).replace(' ', '0');
System.out.println(bt2);
int num3 = num1 << 2;
String bitset13 = Integer.toBinaryString(num3);
bitset13 = String.format("%16s", bitset13)
.replace(' ', '0');
System.out.println(bitset13);
}
}
|
Python3
num1 = 1024
bt1 = bin(num1)[2:].zfill(32)
print(bt1)
num2 = num1 << 1
bt2 = bin(num2)[2:].zfill(32)
print(bt2)
num3 = num1 << 2
bitset13 = bin(num3)[2:].zfill(16)
print(bitset13)
|
C#
using System;
class GFG {
public static void Main(string[] args)
{
int num1 = 1024;
string bt1 = Convert.ToString(num1, 2);
bt1 = bt1.PadLeft(32, '0');
Console.WriteLine(bt1);
int num2 = num1 << 1;
string bt2 = Convert.ToString(num2, 2);
bt2 = bt2.PadLeft(32, '0');
Console.WriteLine(bt2);
int num3 = num1 << 2;
string bitset13 = Convert.ToString(num3, 2);
bitset13 = bitset13.PadLeft(16, '0');
Console.WriteLine(bitset13);
}
}
|
Javascript
let num1 = 1024;
let bt1 = num1.toString(2).padStart(32, '0');
console.log(bt1);
let num2 = num1 << 1;
let bt2 = num2.toString(2).padStart(32, '0');
console.log(bt2);
let num3 = num1 << 2;
let bitset13 = num3.toString(2).padStart(16, '0');
console.log(bitset13);
|
Output
00000000000000000000010000000000
00000000000000000000100000000000
0001000000000000
Time Complexity: O(1)
Auxiliary Space: O(1)
6. Right-Shift (>>)
The right shift operator is denoted by the double right arrow key (>>). The general syntax for the right shift is “shift-expression >> k”. The right-shift operator causes the bits in shift expression to be shifted to the right by the number of positions specified by k. For unsigned numbers, the bit positions that the shift operation has vacated are zero-filled. For signed numbers, the sign bit is used to fill the vacated bit positions. In other words, if the number is positive, 0 is used, and if the number is negative, 1 is used.
Note: Every time we shift a number towards the right by 1 bit it divides that number by 2.
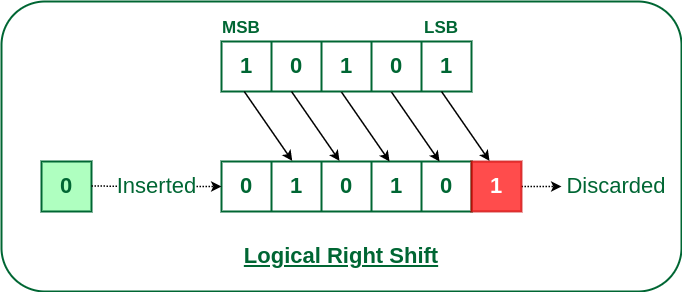
Logical Right Shift
Example:
Input: Right shift of 5 by 1.
Binary representation of 5 = 00101 and Right shift of 00101 by 1 (i.e, 00101 >> 1)

Right shift of 5 by 1
Output: 2
Explanation: All bit of 5 will be shifted by 1 to Rightside and this result in 00010 Which is equivalent to 2
Input: Right shift of 5 by 2.
Binary representation of 5 = 00101 and Right shift of 00101 by 2 (i.e, 00101 >> 2)

Right shift of 5 by 2
Output: 1
Explanation: All bit of 5 will be shifted by 2 to Right side and this result in 00001, Which is equivalent to 1
Input: Right shift of 5 by 3.
Binary representation of 5 = 00101 and Right shift of 00101 by 3 (i.e, 00101 >> 3)

Right shift of 5 by 3
Output: 0
Explanation: All bit of 5 will be shifted by 3 to Right side and this result in 00000, Which is equivalent to 0
Implementation of Right shift operator:
C++
#include <bitset>
#include <iostream>
using namespace std;
int main()
{
unsigned int num1 = 1024;
bitset<32> bt1(num1);
cout << bt1 << endl;
unsigned int num2 = num1 >> 1;
bitset<32> bt2(num2);
cout << bt2 << endl;
unsigned int num3 = num1 >> 2;
bitset<16> bitset13{ num3 };
cout << bitset13 << endl;
}
|
Javascript
let num1 = 1024;
let bt1 = num1.toString(2).padStart(32, '0');
console.log(bt1);
let num2 = num1 >> 1;
let bt2 = num2.toString(2).padStart(32, '0');
console.log(bt2);
let num3 = num1 >> 2;
let bitset13 = num3.toString(2).padStart(16, '0');
console.log(bitset13);
|
Output
00000000000000000000010000000000
00000000000000000000001000000000
0000000100000000
Time Complexity: O(1)
Auxiliary Space: O(1)
Application of BIT Operators
- Bit operations are used for the optimization of embedded systems.
- The Exclusive-or operator can be used to confirm the integrity of a file, making sure it has not been corrupted, especially after it has been in transit.
- Bitwise operations are used in Data encryption and compression.
- Bits are used in the area of networking, framing the packets of numerous bits which are sent to another system generally through any type of serial interface.
- Digital Image Processors use bitwise operations to enhance image pixels and to extract different sections of a microscopic image.
Important Practice Problems on Bitwise Algorithm:
If we want to set a bit at nth position in the number ‘num’, it can be done using the ‘OR’ operator( | ).
- First, we left shift 1 to n position via (1<<n)
- Then, use the “OR” operator to set the bit at that position. “OR” operator is used because it will set the bit even if the bit is unset previously in the binary representation of the number ‘num’.
Note: If the bit would be already set then it would remain unchanged.
Below is the implementation:
C++
#include <iostream>
using namespace std;
void set(int& num, int pos)
{
num |= (1 << pos);
}
int main()
{
int num = 4, pos = 1;
set(num, pos);
cout << (int)(num) << endl;
return 0;
}
|
Java
import java.io.*;
class GFG {
public static void main(String[] args)
{
int num = 4, pos = 1;
num = set(num, pos);
System.out.println(num);
}
public static int set(int num, int pos)
{
num |= (1 << pos);
return num;
}
}
|
Python3
def set(num, pos):
num |= (1 << pos)
print(num)
num, pos = 4, 1
set(num, pos)
|
C#
using System;
public class GFG {
static public void Main()
{
int num = 4, pos = 1;
set(num, pos);
}
static public void set(int num, int pos)
{
num |= (1 << pos);
Console.WriteLine(num);
}
}
|
Javascript
<script>
function set(num,pos)
{
num |= (1 << pos);
console.log(parseInt(num));
}
let num = 4;
let pos = 1;
set(num, pos);
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Suppose we want to unset a bit at nth position in number ‘num’ then we have to do this with the help of “AND” (&) operator.
- First, we left shift ‘1’ to n position via (1<<n) then we use bitwise NOT operator ‘~’ to unset this shifted ‘1’.
- Now after clearing this left shifted ‘1’ i.e making it to ‘0’ we will ‘AND'(&) with the number ‘num’ that will unset bit at nth position.
Below is the implementation:
C++
#include <iostream>
using namespace std;
void unset(int& num, int pos)
{
num &= (~(1 << pos));
}
int main()
{
int num = 7;
int pos = 1;
unset(num, pos);
cout << num << endl;
return 0;
}
|
Java
import java.io.*;
class GFG {
public static void main(String[] args)
{
int num = 7, pos = 1;
num = unset(num, pos);
System.out.println(num);
}
public static int unset(int num, int pos)
{
num = num & (~(1 << pos));
return num;
}
}
|
Python3
def unset(num, pos):
num &= (~(1 << pos))
print(num)
num, pos = 7, 1
unset(num, pos)
|
C#
using System;
public class GFG {
static public void Main()
{
int num = 7, pos = 1;
unset(num, pos);
}
static public void unset(int num, int pos)
{
num &= (~(1 << pos));
Console.WriteLine(num);
}
}
|
Javascript
function unset(num, pos)
{
return num &= (~(1 << pos));
}
let num = 7;
let pos = 1;
console.log(unset(num, pos));
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Toggling means to turn bit ‘on'(1) if it was ‘off'(0) and to turn ‘off'(0) if it was ‘on'(1) previously. We will be using the ‘XOR’ operator here which is this ‘^’. The reason behind the ‘XOR’ operator is because of its properties.
- Properties of ‘XOR’ operator.
- 1^1 = 0
- 0^0 = 0
- 1^0 = 1
- 0^1 = 1
- If two bits are different then the ‘XOR’ operator returns a set bit(1) else it returns an unset bit(0).
Below is the implementation:
C++
#include <iostream>
using namespace std;
void toggle(int& num, int pos) { num ^= (1 << pos); }
int main()
{
int num = 4;
int pos = 1;
toggle(num, pos);
cout << num << endl;
return 0;
}
|
Java
import java.io.*;
class GFG {
public static void main(String[] args)
{
int num = 4, pos = 1;
num = toggle(num, pos);
System.out.println(num);
}
public static int toggle(int num, int pos)
{
num ^= (1 << pos);
return num;
}
}
|
Python3
def toggle(num, pos):
num ^= (1 << pos)
print(num)
num, pos = 4, 1
toggle(num, pos)
|
C#
using System;
public class GFG {
static public void Main()
{
int num = 4, pos = 1;
toggle(num, pos);
}
static public void toggle(int num, int pos)
{
num ^= (1 << pos);
Console.WriteLine(num);
}
}
|
Javascript
function toggle(num, pos){
num ^= (1 << pos)
console.log(num)
}
let num = 4;
let pos = 1;
toggle(num, pos);
|
Time Complexity: O(1)
Auxiliary Space: O(1)
We used the left shift (<<) operation on 1 to shift the bits to nth position and then use the & operation with number given number, and check if it is not-equals to 0.
Below is the implementation:
C++
#include <iostream>
using namespace std;
bool at_position(int num, int pos)
{
bool bit = num & (1 << pos);
return bit;
}
int main()
{
int num = 5;
int pos = 2;
bool bit = at_position(num, pos);
cout << bit << endl;
return 0;
}
|
Java
import java.io.*;
class GFG {
public static void main(String[] args)
{
int num = 5;
int pos = 0;
int bit = at_position(num, pos);
System.out.println(bit);
}
public static int at_position(int num, int pos)
{
int bit = num & (1 << pos);
return bit;
}
}
|
Python3
def at_position(num, pos):
bit = num & (1 << pos)
return bit
num = 5
pos = 0
bit = at_position(num, pos)
print(bit)
|
C#
using System;
public class GFG {
public static bool at_position(int num, int pos)
{
int bit = num & (1 << pos);
if (bit == 0)
return false;
return true;
}
static public void Main()
{
int num = 5;
int pos = 2;
bool bit = at_position(num, pos);
Console.WriteLine(bit);
}
}
|
Javascript
<script>
function at_position(num,pos)
{
return num & (1<<pos);
}
let num = 5;
let pos = 0;
console.log(at_position(num, pos));
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Below is the implementation:
C++
#include <iostream>
using namespace std;
int main()
{
int num = 12;
int ans = num << 1;
cout << ans << endl;
return 0;
}
|
Java
import java.io.*;
class GFG {
public static void main(String[] args)
{
int num = 12;
int ans = num << 1;
System.out.println(ans);
}
}
|
Python3
num = 12
ans = num << 1
print(ans)
|
C#
using System;
public class GFG {
static public void Main()
{
int num = 12;
Console.WriteLine(num << 1);
}
}
|
Javascript
<script>
var num = 12;
var ans = num<<1;
document.write(ans);
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
6. Divide a number 2 using the right shift operator
Below is the implementation:
C++
#include <iostream>
using namespace std;
int main()
{
int num = 12;
int ans = num >> 1;
cout << ans << endl;
return 0;
}
|
Java
import java.io.*;
class GFG {
public static void main(String[] args)
{
int num = 12;
int ans = num >> 1;
System.out.println(ans);
}
}
|
Python3
num = 12
ans = num >> 1
print(ans)
|
C#
using System;
public class GFG {
static public void Main()
{
int num = 12;
Console.WriteLine(num >> 1);
}
}
|
Javascript
<script>
var num = 12;
var ans = num>>1;
document.write(ans);
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
The problem can be solved based on the following observations:
Say x = n % 4. The XOR value depends on the value if x.
If, x = 0, then the answer is n.
x = 1, then answer is 1.
x = 2, then answer is n+1.
x = 3, then answer is 0.
Below is the implementation of the above approach.
C++
int computeXOR(int n)
{
if (n % 4 == 0)
return n;
if (n % 4 == 1)
return 1;
if (n % 4 == 2)
return n + 1;
else
return 0;
}
|
Java
import java.io.*;
class GFG {
public static int computeXOR(int n)
{
if (n % 4 == 0)
return n;
if (n % 4 == 1)
return 1;
if (n % 4 == 2)
return n + 1;
else
return 0;
}
public static void main(String[] args) {}
}
|
Python
def set(num, pos):
num |= (1 << pos)
print(num)
num, pos = 4, 1
set(num, pos)
|
C#
using System;
public class GFG {
public static int computeXOR(int n)
{
if (n % 4 == 0)
return n;
if (n % 4 == 1)
return 1;
if (n % 4 == 2)
return n + 1;
else
return 0;
}
public static void Main() {}
}
|
Javascript
<script>
function computeXOR(n)
{
if (n % 4 == 0)
return n;
if (n % 4 == 1)
return 1;
if (n % 4 == 2)
return n + 1;
else
return 0;
}
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
This can be solved based on the following fact:
If a number N is a power of 2, then the bitwise AND of N and N-1 will be 0. But this will not work if N is 0. So just check these two conditions, if any of these two conditions is true.
Below is the implementation of the above approach.
C++
bool isPowerOfTwo(int x)
{
return x && (!(x & (x - 1)));
}
|
Java
public static boolean isPowerOfTwo(int x)
{
return x != 0 && ((x & (x - 1)) == 0);
}
|
Python
def isPowerOfTwo(x):
return x and (not(x & (x - 1)))
|
C#
using System;
public class GFG {
static public bool isPowerOfTwo(int x)
{
return (x != 0) && ((x & (x - 1)) == 0);
}
static public void Main() {}
}
|
Javascript
function isPowerOfTwo(x)
{
return x && (!(x & (x - 1)));
}
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Counting set bits means, counting total number of 1’s in the binary representation of an integer. For this problem we go through all the bits of given number and check whether it is set or not by performing AND operation (with 1).
Below is the implementation:
C++
int countBits(int n)
{
int count = 0;
while (n) {
count += n & 1;
n >>= 1;
}
return count;
}
|
Java
public static int countBits(int n)
{
int count = 0;
while (n > 0) {
count += n & 1;
n >>= 1;
}
return count;
}
|
Python3
def countBits(n):
count = 0
while n:
count += n & 1
n >>= 1
return count
|
C#
using System;
public class GFG {
public static int countBits(int n)
{
int count = 0;
while (n > 0)
{
count += n & 1;
n >>= 1;
}
return count;
}
static public void Main() {}
}
|
Javascript
function countBits(n)
{
let count = 0;
while (n) {
count += n & 1;
n >>= 1;
}
return count;
}
|
Time Complexity: O(log(n))
Auxiliary Space: O(1)
The idea is to unset the rightmost bit of number n and XOR the result with n. Then the rightmost set bit in n will be the position of the only set bit in the result. Note that if n is odd, we can directly return 1 as the first bit is always set for odd numbers.
Example:
The number 20 in binary is 00010100, and the position of the rightmost set bit is 3.
00010100 & (n = 20)
00010011 (n-1 = 19)
——————-
00010000 ^ (XOR result number with n)
00010100
——————-
00000100 ——-> rightmost set bit will tell us the position
Below is the implementation:
C++
int positionOfRightmostSetBit(int n)
{
if (n & 1) {
return 1;
}
n = n ^ (n & (n - 1));
int pos = 0;
while (n) {
n = n >> 1;
pos++;
}
return pos;
}
|
Java
public static int positionOfRightmostSetBit(int n)
{
if ((n & 1) != 0) {
return 1;
}
n = n ^ (n & (n - 1));
int pos = 0;
while (n != 0) {
n = n >> 1;
pos++;
}
return pos;
}
|
Python
def positionOfRightmostSetBit(n):
if n & 1:
return 1
n = n ^ (n & (n - 1))
pos = 0
while n:
n = n >> 1
pos = pos + 1
return pos
|
C#
public static int positionOfRightmostSetBit(int n)
{
if ((n & 1) != 0) {
return 1;
}
n = n ^ (n & (n - 1));
int pos = 0;
while (n != 0) {
n = n >> 1;
pos++;
}
return pos;
}
|
Javascript
function positionOfRightmostSetBit( n)
{
if (n & 1) {
return 1;
}
n = n ^ (n & (n - 1));
let pos = 0;
while (n) {
n = n >> 1;
pos++;
}
return pos;
}
|
Time Complexity: O(log(n))
Auxiliary Space: O(1)
Related article:
Share your thoughts in the comments
Please Login to comment...