Hopcroft–Karp Algorithm for Maximum Matching | Set 1 (Introduction)
Last Updated :
28 Jun, 2022
A matching in a Bipartite Graph is a set of the edges chosen in such a way that no two edges share an endpoint. A maximum matching is a matching of maximum size (maximum number of edges). In a maximum matching, if any edge is added to it, it is no longer a matching. There can be more than one maximum matching for a given Bipartite Graph.
We have discussed importance of maximum matching and Ford Fulkerson Based approach for maximal Bipartite Matching in previous post. Time complexity of the Ford Fulkerson based algorithm is O(V x E). Hopcroft Karp algorithm is an improvement that runs in O(√V x E) time. Let us define few terms before we discuss the algorithm
Free Node or Vertex: Given a matching M, a node that is not part of matching is called free node. Initially all vertices as free (See first graph of below diagram). In second graph, u2 and v2 are free. In third graph, no vertex is free.
Matching and Not-Matching edges: Given a matching M, edges that are part of matching are called Matching edges and edges that are not part of M (or connect free nodes) are called Not-Matching edges. In first graph, all edges are non-matching. In second graph, (u0, v1), (u1, v0) and (u3, v3) are matching and others not-matching.
Alternating Paths: Given a matching M, an alternating path is a path in which the edges belong alternatively to the matching and not matching. All single edges paths are alternating paths. Examples of alternating paths in middle graph are u0-v1-u2 and u2-v1-u0-v2.
Augmenting path: Given a matching M, an augmenting path is an alternating path that starts from and ends on free vertices. All single edge paths that start and end with free vertices are augmenting paths. In below diagram, augmenting paths are highlighted with blue color. Note that the augmenting path always has one extra matching edge. The Hopcroft Karp algorithm is based on below concept. A matching M is not maximum if there exists an augmenting path. It is also true other way, i.e, a matching is maximum if no augmenting path exists So the idea is to one by one look for augmenting paths. And add the found paths to current matching.
Hopcroft Karp Algorithm:
- Initialize Maximal Matching M as empty.
- While there exists an Augmenting Path p
- Remove matching edges of p from M and add not-matching edges of p to M
- (This increases size of M by 1 as p starts and ends with a free vertex)
- Return M.
Below diagram shows working of the algorithm.
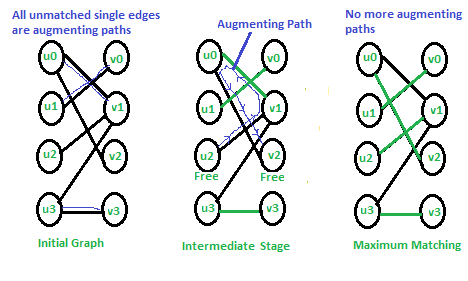
In the initial graph all single edges are augmenting paths and we can pick in any order. In the middle stage, there is only one augmenting path. We remove matching edges of this path from M and add not-matching edges. In final matching, there are no augmenting paths so the matching is maximum.
Implementation of Hopcroft Karp algorithm is discussed in set 2.
Hopcroft–Karp Algorithm for Maximum Matching | Set 2 (Implementation)
Share your thoughts in the comments
Please Login to comment...