Maximum Bipartite Matching
Last Updated :
01 Jun, 2023
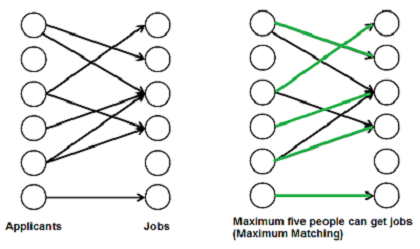
A matching in a Bipartite Graph is a set of the edges chosen in such a way that no two edges share an endpoint. A maximum matching is a matching of maximum size (maximum number of edges). In a maximum matching, if any edge is added to it, it is no longer a matching. There can be more than one maximum matchings for a given Bipartite Graph.
Why do we care?
There are many real world problems that can be formed as Bipartite Matching. For example, consider the following problem:
“There are M job applicants and N jobs. Each applicant has a subset of jobs that he/she is interested in. Each job opening can only accept one applicant and a job applicant can be appointed for only one job. Find an assignment of jobs to applicants in such that as many applicants as possible get jobs.”
We strongly recommend to read the following post first. “Ford-Fulkerson Algorithm for Maximum Flow Problem”
Maximum Bipartite Matching and Max Flow Problem :
Maximum Bipartite Matching (MBP) problem can be solved by converting it into a flow network (See this video to know how did we arrive this conclusion). Following are the steps.

1) Build a Flow Network : There must be a source and sink in a flow network. So we add a source and add edges from source to all applicants. Similarly, add edges from all jobs to sink. The capacity of every edge is marked as 1 unit.

2) Find the maximum flow: We use Ford-Fulkerson algorithm to find the maximum flow in the flow network built in step 1. The maximum flow is actually the MBP we are looking for.
How to implement the above approach?
Let us first define input and output forms. Input is in the form of Edmonds matrix which is a 2D array ‘bpGraph[M][N]’ with M rows (for M job applicants) and N columns (for N jobs). The value bpGraph[i][j] is 1 if i’th applicant is interested in j’th job, otherwise 0.
Output is number maximum number of people that can get jobs.
A simple way to implement this is to create a matrix that represents adjacency matrix representation of a directed graph with M+N+2 vertices. Call the fordFulkerson() for the matrix. This implementation requires O((M+N)*(M+N)) extra space.
Extra space can be reduced and code can be simplified using the fact that the graph is bipartite and capacity of every edge is either 0 or 1. The idea is to use DFS traversal to find a job for an applicant (similar to augmenting path in Ford-Fulkerson). We call bpm() for every applicant, bpm() is the DFS based function that tries all possibilities to assign a job to the applicant.
In bpm(), we one by one try all jobs that an applicant ‘u’ is interested in until we find a job, or all jobs are tried without luck. For every job we try, we do following.
If a job is not assigned to anybody, we simply assign it to the applicant and return true. If a job is assigned to somebody else say x, then we recursively check whether x can be assigned some other job. To make sure that x doesn’t get the same job again, we mark the job ‘v’ as seen before we make recursive call for x. If x can get other job, we change the applicant for job ‘v’ and return true. We use an array maxR[0..N-1] that stores the applicants assigned to different jobs.
If bmp() returns true, then it means that there is an augmenting path in flow network and 1 unit of flow is added to the result in maxBPM().
Implementation:
C++
#include <iostream>
#include <string.h>
using namespace std;
#define M 6
#define N 6
bool bpm(bool bpGraph[M][N], int u,
bool seen[], int matchR[])
{
for (int v = 0; v < N; v++)
{
if (bpGraph[u][v] && !seen[v])
{
seen[v] = true;
if (matchR[v] < 0 || bpm(bpGraph, matchR[v],
seen, matchR))
{
matchR[v] = u;
return true;
}
}
}
return false;
}
int maxBPM(bool bpGraph[M][N])
{
int matchR[N];
memset(matchR, -1, sizeof(matchR));
int result = 0;
for (int u = 0; u < M; u++)
{
bool seen[N];
memset(seen, 0, sizeof(seen));
if (bpm(bpGraph, u, seen, matchR))
result++;
}
return result;
}
int main()
{
bool bpGraph[M][N] = {{0, 1, 1, 0, 0, 0},
{1, 0, 0, 1, 0, 0},
{0, 0, 1, 0, 0, 0},
{0, 0, 1, 1, 0, 0},
{0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 1}};
cout << "Maximum number of applicants that can get job is "
<< maxBPM(bpGraph);
return 0;
}
|
Java
import java.util.*;
import java.lang.*;
import java.io.*;
class GFG
{
static final int M = 6;
static final int N = 6;
boolean bpm(boolean bpGraph[][], int u,
boolean seen[], int matchR[])
{
for (int v = 0; v < N; v++)
{
if (bpGraph[u][v] && !seen[v])
{
seen[v] = true;
if (matchR[v] < 0 || bpm(bpGraph, matchR[v],
seen, matchR))
{
matchR[v] = u;
return true;
}
}
}
return false;
}
int maxBPM(boolean bpGraph[][])
{
int matchR[] = new int[N];
for(int i = 0; i < N; ++i)
matchR[i] = -1;
int result = 0;
for (int u = 0; u < M; u++)
{
boolean seen[] =new boolean[N] ;
for(int i = 0; i < N; ++i)
seen[i] = false;
if (bpm(bpGraph, u, seen, matchR))
result++;
}
return result;
}
public static void main (String[] args)
throws java.lang.Exception
{
boolean bpGraph[][] = new boolean[][]{
{false, true, true,
false, false, false},
{true, false, false,
true, false, false},
{false, false, true,
false, false, false},
{false, false, true,
true, false, false},
{false, false, false,
false, false, false},
{false, false, false,
false, false, true}};
GFG m = new GFG();
System.out.println( "Maximum number of applicants that can"+
" get job is "+m.maxBPM(bpGraph));
}
}
|
Python3
class GFG:
def __init__(self,graph):
self.graph = graph
self.ppl = len(graph)
self.jobs = len(graph[0])
def bpm(self, u, matchR, seen):
for v in range(self.jobs):
if self.graph[u][v] and seen[v] == False:
seen[v] = True
if matchR[v] == -1 or self.bpm(matchR[v],
matchR, seen):
matchR[v] = u
return True
return False
def maxBPM(self):
matchR = [-1] * self.jobs
result = 0
for i in range(self.ppl):
seen = [False] * self.jobs
if self.bpm(i, matchR, seen):
result += 1
return result
bpGraph =[[0, 1, 1, 0, 0, 0],
[1, 0, 0, 1, 0, 0],
[0, 0, 1, 0, 0, 0],
[0, 0, 1, 1, 0, 0],
[0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 1]]
g = GFG(bpGraph)
print ("Maximum number of applicants that can get job is %d " % g.maxBPM())
|
C#
using System;
class GFG
{
static int M = 6;
static int N = 6;
bool bpm(bool [,]bpGraph, int u,
bool []seen, int []matchR)
{
for (int v = 0; v < N; v++)
{
if (bpGraph[u, v] && !seen[v])
{
seen[v] = true;
if (matchR[v] < 0 || bpm(bpGraph, matchR[v],
seen, matchR))
{
matchR[v] = u;
return true;
}
}
}
return false;
}
int maxBPM(bool [,]bpGraph)
{
int []matchR = new int[N];
for(int i = 0; i < N; ++i)
matchR[i] = -1;
int result = 0;
for (int u = 0; u < M; u++)
{
bool []seen = new bool[N] ;
for(int i = 0; i < N; ++i)
seen[i] = false;
if (bpm(bpGraph, u, seen, matchR))
result++;
}
return result;
}
public static void Main ()
{
bool [,]bpGraph = new bool[,]
{{false, true, true,
false, false, false},
{true, false, false,
true, false, false},
{false, false, true,
false, false, false},
{false, false, true,
true, false, false},
{false, false, false,
false, false, false},
{false, false, false,
false, false, true}};
GFG m = new GFG();
Console.Write( "Maximum number of applicants that can"+
" get job is "+m.maxBPM(bpGraph));
}
}
|
PHP
<?php
$M = 6;
$N = 6;
function bpm($bpGraph, $u, &$seen, &$matchR)
{
global $N;
for ($v = 0; $v < $N; $v++)
{
if ($bpGraph[$u][$v] && !$seen[$v])
{
$seen[$v] = true;
if ($matchR[$v] < 0 || bpm($bpGraph, $matchR[$v],
$seen, $matchR))
{
$matchR[$v] = $u;
return true;
}
}
}
return false;
}
function maxBPM($bpGraph)
{
global $N,$M;
$matchR = array_fill(0, $N, -1);
$result = 0;
for ($u = 0; $u < $M; $u++)
{
$seen=array_fill(0, $N, false);
if (bpm($bpGraph, $u, $seen, $matchR))
$result++;
}
return $result;
}
$bpGraph = array(array(0, 1, 1, 0, 0, 0),
array(1, 0, 0, 1, 0, 0),
array(0, 0, 1, 0, 0, 0),
array(0, 0, 1, 1, 0, 0),
array(0, 0, 0, 0, 0, 0),
array(0, 0, 0, 0, 0, 1));
echo "Maximum number of applicants that can get job is ".maxBPM($bpGraph);
?>
|
Javascript
<script>
let M = 6;
let N = 6;
function bpm(bpGraph, u, seen, matchR)
{
for (let v = 0; v < N; v++)
{
if (bpGraph[u][v] && !seen[v])
{
seen[v] = true;
if (matchR[v] < 0 || bpm(bpGraph, matchR[v],
seen, matchR))
{
matchR[v] = u;
return true;
}
}
}
return false;
}
function maxBPM(bpGraph)
{
let matchR = new Array(N);
for(let i = 0; i < N; ++i)
matchR[i] = -1;
let result = 0;
for (let u = 0; u < M; u++)
{
let seen =new Array(N);
for(let i = 0; i < N; ++i)
seen[i] = false;
if (bpm(bpGraph, u, seen, matchR))
result++;
}
return result;
}
let bpGraph = [
[false, true, true,
false, false, false],
[true, false, false,
true, false, false],
[false, false, true,
false, false, false],
[false, false, true,
true, false, false],
[false, false, false,
false, false, false],
[false, false, false,
false, false, true]];
document.write( "Maximum number of applicants that can"+
" get job is "+ maxBPM(bpGraph));
</script>
|
Output
Maximum number of applicants that can get job is 5
Time Complexity: O(V*E)
The time complexity of the above algorithm is O(V*E) where V is the number of vertices in the graph and E is the number of edges. The algorithm iterates over each vertex in the graph and then performs a DFS on the corresponding edges to find the maximum bipartite matching.
Space Complexity: O(V + E)
The space complexity of this algorithm is O(V + E) as it uses a two-dimensional boolean array to store the graph and an array to store the maximum matching.
You may like to see below also:
Hopcroft–Karp Algorithm for Maximum Matching | Set 1 (Introduction)
Hopcroft–Karp Algorithm for Maximum Matching | Set 2 (Implementation)
Share your thoughts in the comments
Please Login to comment...