Fibonacci Series
Last Updated :
29 Feb, 2024
Ever wondered about the cool math behind the Fibonacci series? This simple pattern has a remarkable presence in nature, from the arrangement of leaves on plants to the spirals of seashells. We’re diving into this Fibonacci Series sequence. It’s not just math, it’s in art, nature, and more! Let’s discover the secrets of the Fibonacci series together.
What is the Fibonacci Series?
The Fibonacci series is the sequence where each number is the sum of the previous two numbers of the sequence. The first two numbers of the Fibonacci series are 0 and 1 and are used to generate the Fibonacci series.
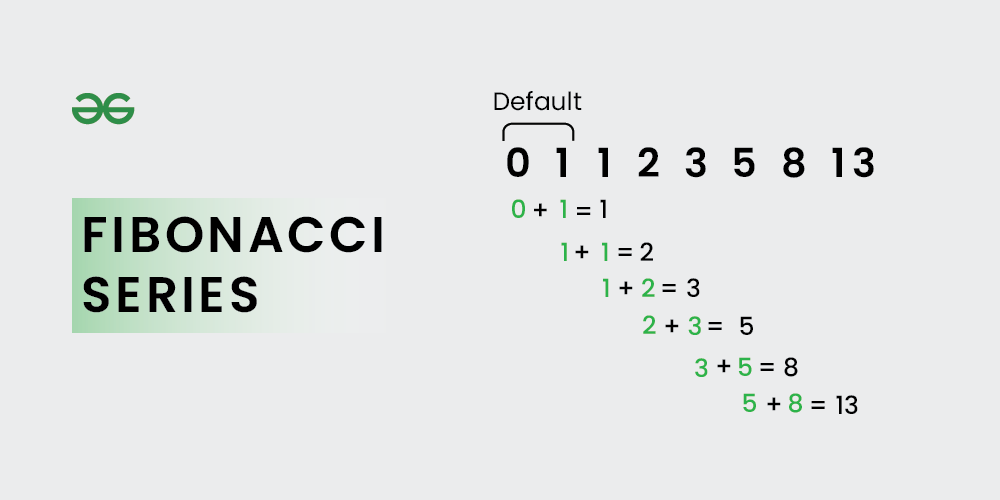
Fibonacci Series
How to Find the Nth term of Fibonacci Series?
In mathematical terms, the number at the nth position can be represented by:
Fn = Fn-1 + Fn-2
where, F0 = 0 and F1 = 1.
For example, Fibonacci series upto 10 terms is: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34
Program to print first N term of Fibonacci Series:
1. Print Fibonacci series using Recursion:
In this method, we will use a function that prints the first two terms, and the rest of the terms are then handled by the other function that makes use of a recursive technique to print the next terms of the sequence.
Below is the implementation of the above idea:
C++
#include <iostream>
using namespace std;
int prev1 = 1;
int prev2 = 0;
void fib(int n)
{
if (n < 3) {
return;
}
int fn = prev1 + prev2;
prev2 = prev1;
prev1 = fn;
cout << fn << " ";
return fib(n - 1);
}
void printFib(int n)
{
if (n < 1) {
cout << "Invalid number of terms\n";
}
else if (n == 1) {
cout << 0;
}
else if (n == 2) {
cout << "0 1";
}
else {
cout << "0 1 ";
fib(n);
}
return;
}
int main()
{
int n = 9;
printFib(n);
return 0;
}
|
Java
import java.io.*;
public class FibonacciSeries {
static void fib(int n, int prev1, int prev2) {
if (n < 3) {
return;
}
int fn = prev1 + prev2;
prev2 = prev1;
prev1 = fn;
System.out.print(fn + " ");
fib(n - 1, prev1, prev2);
}
static void printFib(int n) {
if (n < 1) {
System.out.println("Invalid number of terms");
}
else if (n == 1) {
System.out.println(0);
}
else if (n == 2) {
System.out.println("0 1");
}
else {
System.out.print("0 1 ");
fib(n, 1, 0);
}
}
public static void main(String[] args) {
int n = 9;
printFib(n);
}
}
|
Python3
def fib(n, prev1, prev2):
if n < 3:
return
fn = prev1 + prev2
prev2 = prev1
prev1 = fn
print(fn, end=" ")
fib(n - 1, prev1, prev2)
def print_fib(n):
if n < 1:
print("Invalid number of terms")
elif n == 1:
print(0)
elif n == 2:
print("0 1")
else:
print("0 1", end=" ")
fib(n, 1, 0)
if __name__ == "__main__":
n = 9
print_fib(n)
|
C#
using System;
class Program
{
static int prev1 = 1;
static int prev2 = 0;
static void Fib(int n)
{
if (n < 3)
{
return;
}
int fn = prev1 + prev2;
prev2 = prev1;
prev1 = fn;
Console.Write(fn + " ");
Fib(n - 1);
}
static void PrintFib(int n)
{
if (n < 1)
{
Console.WriteLine("Invalid number of terms");
}
else if (n == 1)
{
Console.WriteLine(0);
}
else if (n == 2)
{
Console.WriteLine("0 1");
}
else
{
Console.Write("0 1 ");
Fib(n);
}
}
static void Main()
{
int n = 9;
PrintFib(n);
}
}
|
Javascript
function fib(n, prev1, prev2) {
if (n < 3) {
return;
}
let fn = prev1 + prev2;
prev2 = prev1;
prev1 = fn;
process.stdout.write(fn + " ");
fib(n - 1, prev1, prev2);
}
function printFib(n) {
if (n < 1) {
console.log("Invalid number of terms");
}
else if (n === 1) {
console.log(0);
}
else if (n === 2) {
console.log("0 1");
}
else {
process.stdout.write("0 1 ");
fib(n, 1, 0);
}
}
const n = 9;
printFib(n);
|
Complexity Analysis:
- Time complexity: O(n), It is because, for printing n terms, the fib() function will call itself recursively for (n – 2) times and each time it will take constant time.
- Auxiliary Space: O(n), It is because, for each recursive call of the fib() function, a separate stack frame is created. For (n-2) calls, (n-2) stack frames are created with results in the O(n) space complexity.
2. Fibonacci series using loops
In this method, we use one of the C loops to iterate and print the current term. The first two terms, F1 and F2 are handled separately. After that, we use two variables to store the previous two terms and keep updating them as we move to print the next term.
Below is the implementation of the above idea:
C++
#include <iostream>
using namespace std;
void printFib(int n)
{
if (n < 1) {
cout << "Invalid Number of terms\n";
return;
}
int prev1 = 1;
int prev2 = 0;
for (int i = 1; i <= n; i++) {
if (i > 2) {
int num = prev1 + prev2;
prev2 = prev1;
prev1 = num;
cout << num << " ";
}
if (i == 1) {
cout << prev2 << " ";
}
if (i == 2) {
cout << prev1 << " ";
}
}
}
int main()
{
int n = 9;
printFib(n);
return 0;
}
|
Java
public class FibonacciSeries {
static void printFib(int n) {
if (n < 1) {
System.out.println("Invalid Number of terms");
return;
}
int prev1 = 1;
int prev2 = 0;
for (int i = 1; i <= n; i++) {
if (i > 2) {
int num = prev1 + prev2;
prev2 = prev1;
prev1 = num;
System.out.print(num + " ");
}
if (i == 1) {
System.out.print(prev2 + " ");
}
if (i == 2) {
System.out.print(prev1 + " ");
}
}
}
public static void main(String[] args) {
int n = 9;
printFib(n);
}
}
|
Python3
def print_fib(n):
if n < 1:
print("Invalid Number of terms")
return
prev1 = 1
prev2 = 0
for i in range(1, n + 1):
if i > 2:
num = prev1 + prev2
prev2 = prev1
prev1 = num
print(num, end=" ")
if i == 1:
print(prev2, end=" ")
if i == 2:
print(prev1, end=" ")
n = 9
print_fib(n)
|
C#
using System;
class Program
{
static void PrintFib(int n)
{
if (n < 1)
{
Console.WriteLine("Invalid Number of terms");
return;
}
int prev1 = 1;
int prev2 = 0;
for (int i = 1; i <= n; i++)
{
if (i > 2)
{
int num = prev1 + prev2;
prev2 = prev1;
prev1 = num;
Console.Write(num + " ");
}
if (i == 1)
{
Console.Write(prev2 + " ");
}
if (i == 2)
{
Console.Write(prev1 + " ");
}
}
}
static void Main(string[] args)
{
int n = 9;
PrintFib(n);
}
}
|
Javascript
function printFib(n) {
if (n < 1) {
console.log("Invalid Number of terms");
return;
}
let prev1 = 1;
let prev2 = 0;
for (let i = 1; i <= n; i++) {
if (i > 2) {
const num = prev1 + prev2;
prev2 = prev1;
prev1 = num;
console.log(num + " ");
}
if (i === 1) {
console.log(prev2 + " ");
}
if (i === 2) {
console.log(prev1 + " ");
}
}
console.log();
}
const n = 9;
printFib(n);
|
Complexity Analysis
- Time Complexity: O(n), Because for n number for terms, the loop inside the printFib() function will be executed n times.
- Auxiliary Space: O(1), Because we only used a few variables which don’t depends on the number of terms to be printed
Relation Between Pascal triangle and Fibonacci numbers:
Pascal’s triangle is the arrangement of the data in triangular form which is used to represent the coefficients of the binomial expansions, i.e. the second row in Pascal’s triangle represents the coefficients in (x+y)2 and so on. In Pascal’s triangle, each number is the sum of the above two numbers. Pascal’s triangle has various applications in probability theory, combinatorics, algebra, and various other branches of mathematics.
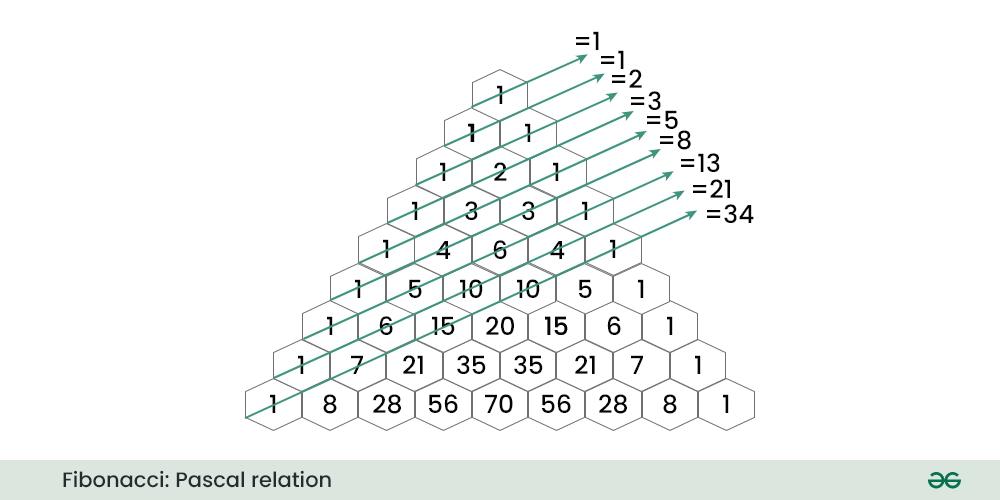
As shown in the image the diagonal sum of the pascal’s triangle forms a fibonacci sequence.
Mathematically: [Tex]\Sigma_{k=0}^{\left \lfloor n/2 \right \rfloor} \binom{n-k}{k} = F_{n+1}
[/Tex]
where [Tex]F_{t}
[/Tex] is the t-th term of the Fibonacci sequence.
Golden Ratio:
Definition: The golden ratio, often denoted by the Greek letter phi (Φ) or the mathematical symbol τ (tau), is a special mathematical constant that has been of interest to mathematicians, scientists, artists, and architects for centuries. It is an irrational number, meaning its decimal representation goes on forever without repeating, and it is approximately equal to 1.6180339887…
The below image shows how the division of consecutive Fibonacci number forms a Golden Ratio i.e,
- x-axis : F(n+1)/F(n), where F( ) represents a Fibonacci number.
- y-axis : represents the value of the fraction obtained in x-axis.
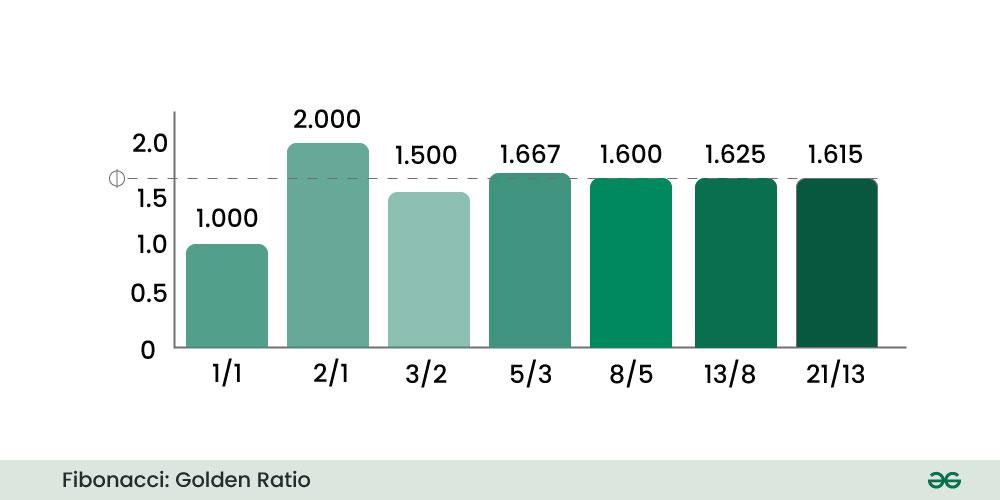
The ratio of successive Fibonacci numbers approximates the golden ratio, and this relationship becomes more accurate as you move further along the Fibonacci sequence.
Fibonacci Spiral:
The Fibonacci spiral is created using a series of quarter circles, with radii that correspond to the Fibonacci numbers as shown in below image: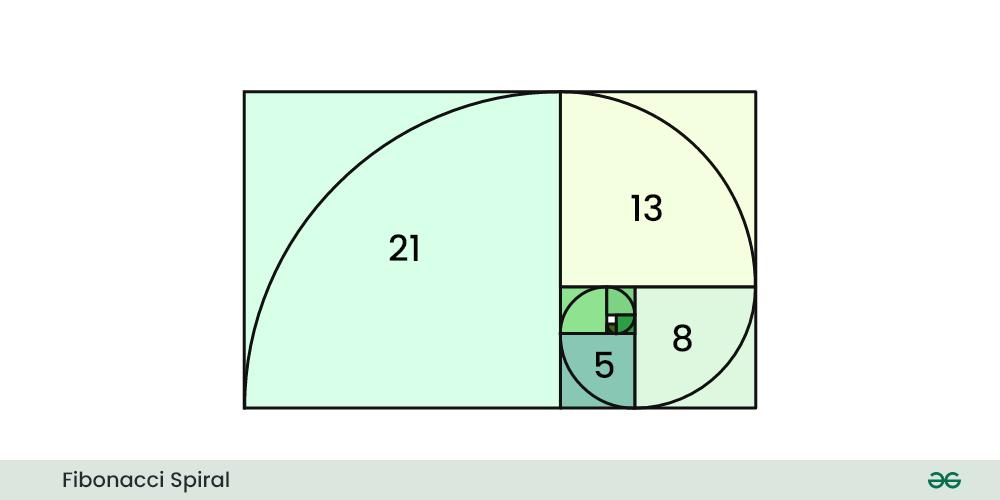
The resulting spiral is known as a “Fibonacci spiral” or a “Golden Spiral” It is often associated with the Golden Ratio, which is an irrational number approximately equal to 1.61803398875. The Fibonacci spiral is considered visually pleasing and can be found in various aspects of art, architecture, and nature due to its aesthetic qualities and mathematical significance.
Problems based on Fibonacci Number/Series:
Some Facts about Fibonacci Numbers:
- The Fibonacci numbers were first mentioned in Indian mathematics in a work by Pingala on enumerating potential patterns of Sanskrit poetry built from syllables of two lengths. The numbers were named after the Italian mathematician Leonardo of Pisa, also known as Fibonacci.
- The Fibonacci sequence and the golden ratio are often found in natural patterns, such as the arrangement of leaves on a stem, the spirals of a pinecone, the seeds in a sunflower, and in art and architecture, like the Parthenon in Athens.
- November 23 is Fibonacci Day as it forms the first 4 digits of fibonacci numbers 11/23.
- Honey bees’ family tree follows fibonacci sequence.
Applications of Fibonacci Number/Series:
- Mile to kilometre approximation : If a distance in miles is a fibonacci number then the succeeding fibonacci number is its kilmometer representation. Example: If we take a number from Fibonacci series i.e., 13 then the kilometre value will be 20.9215 by formulae, which is nearly 21 by rounding.
- Financial Analysis: In the field of technical analysis in finance, Fibonacci retracement is a popular tool used to identify potential levels of support and resistance in stock and commodity price charts.
- Art and Design: The golden ratio, which is closely related to Fibonacci numbers, is often used in art and design to create aesthetically pleasing proportions and layouts. It can be seen in architecture, paintings, and sculptures.
- Data Structures and Algorithms: Fibonacci heaps, a type of data structure in computer science, are used in certain algorithms, such as Dijkstra’s algorithm, for efficient graph processing.
Share your thoughts in the comments
Please Login to comment...