Python Program for n-th Fibonacci number

In mathematical terms, the sequence Fn of Fibonacci numbers is defined by the recurrence relation 

Fn = Fn-1 + Fn-2

With seed values 

F0 = 0 and F1 = 1.

Method 1 ( Use recursion ) :

Python3

# Function for nth Fibonacci number

def Fibonacci(n):
    if n<= 0:
        print("Incorrect input")
    # First Fibonacci number is 0
    elif n == 1:
        return 0
    # Second Fibonacci number is 1
    elif n == 2:
        return 1
    else:
        return Fibonacci(n-1)+Fibonacci(n-2)

# Driver Program

print(Fibonacci(10))

# This code is contributed by Saket Modi

Output

34

Time Complexity: O(2^N)
Auxiliary Space: O(N)

Method 2 ( Use Dynamic Programming ) : 

Python3

# Function for nth fibonacci number - Dynamic Programming
# Taking 1st two fibonacci numbers as 0 and 1

FibArray = [0, 1]

def fibonacci(n):
    if n<0:
        print("Incorrect input")
    elif n<= len(FibArray):
        return FibArray[n-1]
    else:
        temp_fib = fibonacci(n-1)+fibonacci(n-2)
        FibArray.append(temp_fib)
        return temp_fib

# Driver Program

print(fibonacci(9))

# This code is contributed by Saket Modi

Output

21

Time Complexity: O(N)
Auxiliary Space: O(N)

Method 3 ( Use Dynamic Programming with Space Optimization) :

Python3

# Function for nth fibonacci number - Space Optimisation
# Taking 1st two fibonacci numbers as 0 and 1

def fibonacci(n):
    a = 0
    b = 1
    if n < 0:
        print("Incorrect input")
    elif n == 0:
        return a
    elif n == 1:
        return b
    else:
        for i in range(2, n):
            c = a + b
            a = b
            b = c
        return b

# Driver Program

print(fibonacci(9))

# This code is contributed by Saket Modi

Output

21

Time Complexity: O(N)
Auxiliary Space: O(1)

Method 4 ( Using Arrays ) :

Python3

# creating an array in the function to find the
#nth number in fibonacci series. [0, 1, 1, ...]
def fibonacci(n):
    if n <= 0:
        return "Incorrect Output"
    data = [0, 1]
    if n > 2:
        for i in range(2, n):
            data.append(data[i-1] + data[i-2])
    return data[n-1]

# Driver Program
print(fibonacci(9))

# This Code is contributed by Prasun Parate (prasun_parate)

Output

21

Time Complexity: O(N)
Auxiliary Space: O(N)

Explanation:

[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144]
As we know that the Fibonacci series is the sum of the previous two terms, so if we enter 12 as the input in the program, so we should get 144 as the output. And that is what is the result. 

Method 5 ( Using Direct Formula ) : 

The formula for finding the n-th Fibonacci number is as follows:

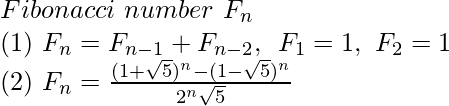
Python3

# To find the n-th Fibonacci Number using formula
from math import sqrt
# import square-root method from math library
def nthFib(n):
    res = (((1+sqrt(5))**n)-((1-sqrt(5)))**n)/(2**n*sqrt(5))
    # compute the n-th fibonacci number
    print(int(res),'is',str(n)+'th fibonacci number')
    # format and print the number

# driver code
nthFib(12)

# This code is contributed by Kush Mehta

Output

144 is 12th fibonacci number

Time Complexity: O(1)
Auxiliary Space: O(1)

Method 6: Using power of the matrix {{1, 1}, {1, 0}}

This is another O(n) that relies on the fact that if we n times multiply the matrix M = {{1,1},{1,0}} to itself (in other words calculate power(M, n)), then we get the (n+1)th Fibonacci number as the element at row and column (0, 0) in the resultant matrix.
The matrix representation gives the following closed expression for the Fibonacci numbers: 

Python

# Helper function that multiplies
# 2 matrices F and M of size 2*2,
# and puts the multiplication
# result back to F[][]

# Helper function that calculates
# F[][] raise to the power n and
# puts the result in F[][]
# Note that this function is
# designed only for fib() and
# won't work as general
# power function
def fib(n):
    F = [[1, 1],
         [1, 0]]
    if (n == 0):
        return 0
    power(F, n - 1)
    return F[0][0]


def multiply(F, M):
  x = (F[0][0] * M[0][0] + F[0][1] * M[1][0])
  y = (F[0][0] * M[0][1] + F[0][1] * M[1][1])
  z = (F[1][0] * M[0][0] + F[1][1] * M[1][0])
  w = (F[1][0] * M[0][1] + F[1][1] * M[1][1])
  F[0][0] = x
  F[0][1] = y
  F[1][0] = z
  F[1][1] = w


def power(F, n):
    M = [[1, 1], [1, 0]]
    # n - 1 times multiply the
    # matrix to {{1,0},{0,1}}
    for i in range(2, n + 1):
        multiply(F, M)


# Driver Code
if __name__ == "__main__":
    n = 9
    print(fib(n))

# This code is contributed by Yash Agarwal

Output

34

Time Complexity: O(n) 
Auxiliary Space: O(1)

Method 7: Optimization of method 6

Method 6 can be optimized to work in O(Logn) time complexity. We can do recursive multiplication to get power(M, n) in the previous method.

Steps:

1. To optimize method 6, we need to just change the power function of the method 6.
2. In method 6, the power function takes O(n) time for which the time complexity of the whole program becomes O(n).
3. In this method, we modify the power function using recursion, calling (F and n//2) which makes n half at each calling and achieve time complexity of O(log N).

Python3

# Nth Fibonacci Number using
# optimized power of the matrix method

# function that returns nth
# Fibonacci number


def fib(n):
    F = [[1, 1],
         [1, 0]]
    if (n == 0):
        return 0
    power(F, n - 1)

    return F[0][0]


def multiply(F, M):
    x = (F[0][0] * M[0][0] +
         F[0][1] * M[1][0])
    y = (F[0][0] * M[0][1] +
         F[0][1] * M[1][1])
    z = (F[1][0] * M[0][0] +
         F[1][1] * M[1][0])
    w = (F[1][0] * M[0][1] +
         F[1][1] * M[1][1])

    F[0][0] = x
    F[0][1] = y
    F[1][0] = z
    F[1][1] = w

# Optimized version of
# power() in method 6


def power(F, n):
    if(n == 0 or n == 1):
        return
    M = [[1, 1],
         [1, 0]]

    power(F, n // 2)
    multiply(F, F)

    if (n % 2 != 0):
        multiply(F, M)


# Driver Code
if __name__ == "__main__":
    n = 5
    print(fib(n))

Output

5

Time Complexity: O(log N)
Auxiliary Space: O(log N), if we consider the function call stack size, otherwise O(1).

Please refer complete article on Program for Fibonacci numbers for more details!