Fibonacci Search
Last Updated :
11 Oct, 2023
Given a sorted array arr[] of size n and an element x to be searched in it. Return index of x if it is present in array else return -1.
Examples:
Input: arr[] = {2, 3, 4, 10, 40}, x = 10
Output: 3
Element x is present at index 3.
Input: arr[] = {2, 3, 4, 10, 40}, x = 11
Output: -1
Element x is not present.
Fibonacci Search is a comparison-based technique that uses Fibonacci numbers to search an element in a sorted array.
Similarities with Binary Search:
- Works for sorted arrays
- A Divide and Conquer Algorithm.
- Has Log n time complexity.
Differences with Binary Search:
- Fibonacci Search divides given array into unequal parts
- Binary Search uses a division operator to divide range. Fibonacci Search doesn’t use /, but uses + and -. The division operator may be costly on some CPUs.
- Fibonacci Search examines relatively closer elements in subsequent steps. So when the input array is big that cannot fit in CPU cache or even in RAM, Fibonacci Search can be useful.
Background:
Fibonacci Numbers are recursively defined as F(n) = F(n-1) + F(n-2), F(0) = 0, F(1) = 1. First few Fibonacci Numbers are 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
Observations:
Below observation is used for range elimination, and hence for the O(log(n)) complexity.
F(n - 2) ≈ (1/3)*F(n) and
F(n - 1) ≈ (2/3)*F(n).
Algorithm:
Let the searched element be x.
The idea is to first find the smallest Fibonacci number that is greater than or equal to the length of the given array. Let the found Fibonacci number be fib (m’th Fibonacci number). We use (m-2)’th Fibonacci number as the index (If it is a valid index). Let (m-2)’th Fibonacci Number be i, we compare arr[i] with x, if x is same, we return i. Else if x is greater, we recur for subarray after i, else we recur for subarray before i.
Below is the complete algorithm
Let arr[0..n-1] be the input array and the element to be searched be x.
- Find the smallest Fibonacci Number greater than or equal to n. Let this number be fibM [m’th Fibonacci Number]. Let the two Fibonacci numbers preceding it be fibMm1 [(m-1)’th Fibonacci Number] and fibMm2 [(m-2)’th Fibonacci Number].
- While the array has elements to be inspected:
- Compare x with the last element of the range covered by fibMm2
- If x matches, return index
- Else If x is less than the element, move the three Fibonacci variables two Fibonacci down, indicating elimination of approximately rear two-third of the remaining array.
- Else x is greater than the element, move the three Fibonacci variables one Fibonacci down. Reset offset to index. Together these indicate the elimination of approximately front one-third of the remaining array.
- Since there might be a single element remaining for comparison, check if fibMm1 is 1. If Yes, compare x with that remaining element. If match, return index.
C++
#include <bits/stdc++.h>
using namespace std;
int min(int x, int y) { return (x <= y) ? x : y; }
int fibMonaccianSearch(int arr[], int x, int n)
{
int fibMMm2 = 0;
int fibMMm1 = 1;
int fibM = fibMMm2 + fibMMm1;
while (fibM < n) {
fibMMm2 = fibMMm1;
fibMMm1 = fibM;
fibM = fibMMm2 + fibMMm1;
}
int offset = -1;
while (fibM > 1) {
int i = min(offset + fibMMm2, n - 1);
if (arr[i] < x) {
fibM = fibMMm1;
fibMMm1 = fibMMm2;
fibMMm2 = fibM - fibMMm1;
offset = i;
}
else if (arr[i] > x) {
fibM = fibMMm2;
fibMMm1 = fibMMm1 - fibMMm2;
fibMMm2 = fibM - fibMMm1;
}
else
return i;
}
if (fibMMm1 && arr[offset + 1] == x)
return offset + 1;
return -1;
}
int main()
{
int arr[]
= { 10, 22, 35, 40, 45, 50, 80, 82, 85, 90, 100,235};
int n = sizeof(arr) / sizeof(arr[0]);
int x = 235;
int ind = fibMonaccianSearch(arr, x, n);
if(ind>=0)
cout << "Found at index: " << ind;
else
cout << x << " isn't present in the array";
return 0;
}
|
C
#include <stdio.h>
int min(int x, int y) { return (x <= y) ? x : y; }
int fibMonaccianSearch(int arr[], int x, int n)
{
int fibMMm2 = 0;
int fibMMm1 = 1;
int fibM = fibMMm2 + fibMMm1;
while (fibM < n) {
fibMMm2 = fibMMm1;
fibMMm1 = fibM;
fibM = fibMMm2 + fibMMm1;
}
int offset = -1;
while (fibM > 1) {
int i = min(offset + fibMMm2, n - 1);
if (arr[i] < x) {
fibM = fibMMm1;
fibMMm1 = fibMMm2;
fibMMm2 = fibM - fibMMm1;
offset = i;
}
else if (arr[i] > x) {
fibM = fibMMm2;
fibMMm1 = fibMMm1 - fibMMm2;
fibMMm2 = fibM - fibMMm1;
}
else
return i;
}
if (fibMMm1 && arr[offset + 1] == x)
return offset + 1;
return -1;
}
int main(void)
{
int arr[]
= { 10, 22, 35, 40, 45, 50, 80, 82, 85, 90, 100,235};
int n = sizeof(arr) / sizeof(arr[0]);
int x = 235;
int ind = fibMonaccianSearch(arr, x, n);
if(ind>=0)
printf("Found at index: %d",ind);
else
printf("%d isn't present in the array",x);
return 0;
}
|
Java
import java.util.*;
class Fibonacci {
public static int min(int x, int y)
{
return (x <= y) ? x : y;
}
public static int fibMonaccianSearch(int arr[], int x,
int n)
{
int fibMMm2 = 0;
int fibMMm1 = 1;
int fibM = fibMMm2 + fibMMm1;
while (fibM < n) {
fibMMm2 = fibMMm1;
fibMMm1 = fibM;
fibM = fibMMm2 + fibMMm1;
}
int offset = -1;
while (fibM > 1) {
int i = min(offset + fibMMm2, n - 1);
if (arr[i] < x) {
fibM = fibMMm1;
fibMMm1 = fibMMm2;
fibMMm2 = fibM - fibMMm1;
offset = i;
}
else if (arr[i] > x) {
fibM = fibMMm2;
fibMMm1 = fibMMm1 - fibMMm2;
fibMMm2 = fibM - fibMMm1;
}
else
return i;
}
if (fibMMm1 == 1 && arr[n-1] == x)
return n-1;
return -1;
}
public static void main(String[] args)
{
int arr[] = { 10, 22, 35, 40, 45, 50,
80, 82, 85, 90, 100,235};
int n = 12;
int x = 235;
int ind = fibMonaccianSearch(arr, x, n);
if(ind>=0)
System.out.print("Found at index: "
+ind);
else
System.out.print(x+" isn't present in the array");
}
}
|
Python3
from bisect import bisect_left
def fibMonaccianSearch(arr, x, n):
fibMMm2 = 0
fibMMm1 = 1
fibM = fibMMm2 + fibMMm1
while (fibM < n):
fibMMm2 = fibMMm1
fibMMm1 = fibM
fibM = fibMMm2 + fibMMm1
offset = -1
while (fibM > 1):
i = min(offset+fibMMm2, n-1)
if (arr[i] < x):
fibM = fibMMm1
fibMMm1 = fibMMm2
fibMMm2 = fibM - fibMMm1
offset = i
elif (arr[i] > x):
fibM = fibMMm2
fibMMm1 = fibMMm1 - fibMMm2
fibMMm2 = fibM - fibMMm1
else:
return i
if(fibMMm1 and arr[n-1] == x):
return n-1
return -1
arr = [10, 22, 35, 40, 45, 50,
80, 82, 85, 90, 100,235]
n = len(arr)
x = 235
ind = fibMonaccianSearch(arr, x, n)
if ind>=0:
print("Found at index:",ind)
else:
print(x,"isn't present in the array");
|
C#
using System;
class GFG {
public static int min(int x, int y)
{
return (x <= y) ? x : y;
}
public static int fibMonaccianSearch(int[] arr, int x,
int n)
{
int fibMMm2 = 0;
int fibMMm1 = 1;
int fibM = fibMMm2 + fibMMm1;
while (fibM < n) {
fibMMm2 = fibMMm1;
fibMMm1 = fibM;
fibM = fibMMm2 + fibMMm1;
}
int offset = -1;
while (fibM > 1) {
int i = min(offset + fibMMm2, n - 1);
if (arr[i] < x) {
fibM = fibMMm1;
fibMMm1 = fibMMm2;
fibMMm2 = fibM - fibMMm1;
offset = i;
}
else if (arr[i] > x) {
fibM = fibMMm2;
fibMMm1 = fibMMm1 - fibMMm2;
fibMMm2 = fibM - fibMMm1;
}
else
return i;
}
if (fibMMm1 == 1 && arr[n-1] == x)
return n-1;
return -1;
}
public static void Main()
{
int[] arr = { 10, 22, 35, 40, 45, 50,
80, 82, 85, 90, 100,235 };
int n = 12;
int x = 235;
int ind = fibMonaccianSearch(arr, x, n);
if(ind>=0)
Console.Write("Found at index: "+ind);
else
Console.Write(x+" isn't present in the array");
}
}
|
PHP
<?php
function fibMonaccianSearch($arr, $x, $n)
{
$fibMMm2 = 0;
$fibMMm1 = 1;
$fibM = $fibMMm2 + $fibMMm1;
while ($fibM < $n)
{
$fibMMm2 = $fibMMm1;
$fibMMm1 = $fibM;
$fibM = $fibMMm2 + $fibMMm1;
}
$offset = -1;
while ($fibM > 1)
{
$i = min($offset+$fibMMm2, $n-1);
if ($arr[$i] < $x)
{
$fibM = $fibMMm1;
$fibMMm1 = $fibMMm2;
$fibMMm2 = $fibM - $fibMMm1;
$offset = $i;
}
else if ($arr[$i] > $x)
{
$fibM = $fibMMm2;
$fibMMm1 = $fibMMm1 - $fibMMm2;
$fibMMm2 = $fibM - $fibMMm1;
}
else return $i;
}
if($fibMMm1 && $arr[$n-1] == $x)return $n-1;
return -1;
}
$arr = array(10, 22, 35, 40, 45, 50, 80, 82,85, 90, 100,235);
$n = count($arr);
$x = 235;
$ind = fibMonaccianSearch($arr, $x, $n);
if($ind>=0)
printf("Found at index: ".$ind);
else
printf($x." isn't present in the array");
?>
|
Javascript
<script>
function fibMonaccianSearch(arr, x, n)
{
let fibMMm2 = 0;
let fibMMm1 = 1;
let fibM = fibMMm2 + fibMMm1;
while (fibM < n)
{
fibMMm2 = fibMMm1;
fibMMm1 = fibM;
fibM = fibMMm2 + fibMMm1;
}
let offset = -1;
while (fibM > 1)
{
let i = Math.min(offset + fibMMm2, n-1);
if (arr[i] < x)
{
fibM = fibMMm1;
fibMMm1 = fibMMm2;
fibMMm2 = fibM - fibMMm1;
offset = i;
}
else if (arr[i] > x)
{
fibM = fibMMm2;
fibMMm1 = fibMMm1 - fibMMm2;
fibMMm2 = fibM - fibMMm1;
}
else return i;
}
if(fibMMm1 && arr[n-1] == x){
return n-1
}
return -1;
}
let arr = [10, 22, 35, 40, 45, 50, 80, 82,85, 90, 100,235];
let n = arr.length;
let x = 235;
let ind = fibMonaccianSearch(arr, x, n);
if(ind>=0){
document.write("Found at index: " + ind);
}else{
document.write(x + " isn't present in the array");
}
</script>
|
Output
Found at index: 11
Illustration:
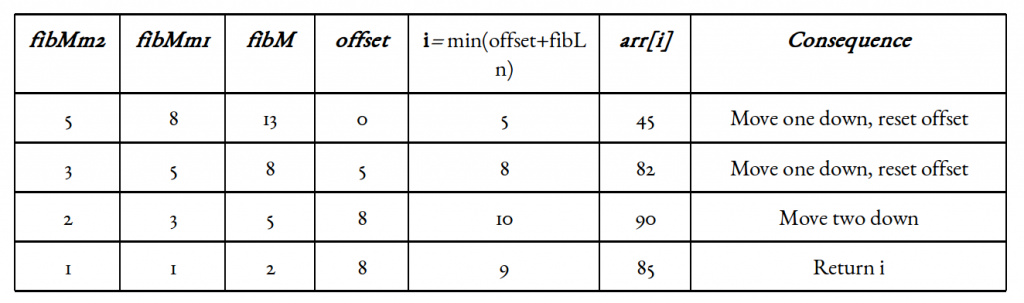
Let us understand the algorithm with the below example:

Illustration assumption: 1-based indexing. Target element x is 85. Length of array n = 11.
Smallest Fibonacci number greater than or equal to 11 is 13. As per our illustration, fibMm2 = 5, fibMm1 = 8, and fibM = 13.
Another implementation detail is the offset variable (zero-initialized). It marks the range that has been eliminated, starting from the front. We will update it from time to time.
Now since the offset value is an index and all indices including it and below it have been eliminated, it only makes sense to add something to it. Since fibMm2 marks approximately one-third of our array, as well as the indices it marks, are sure to be valid ones, we can add fibMm2 to offset and check the element at index i = min(offset + fibMm2, n).
Visualization:
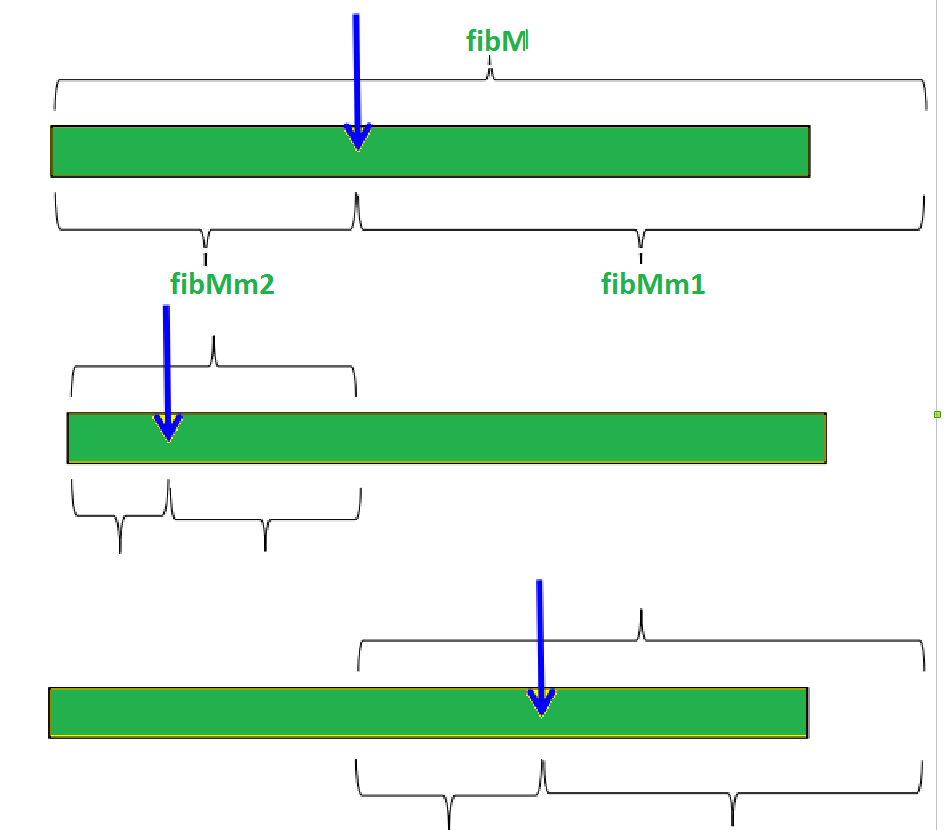
Time Complexity analysis:
The worst-case will occur when we have our target in the larger (2/3) fraction of the array, as we proceed to find it. In other words, we are eliminating the smaller (1/3) fraction of the array every time. We call once for n, then for(2/3) n, then for (4/9) n, and henceforth.
Consider that:

Auxiliary Space: O(1)
References:
https://en.wikipedia.org/wiki/Fibonacci_search_technique
Approach 2: Iterative implementation
Fibonacci Search is a searching algorithm used to find the position of an element in a sorted array. The basic idea behind Fibonacci Search is to use Fibonacci numbers to determine the split points in the array and perform binary search on the appropriate subarray.
Here’s a Python implementation of Fibonacci Search using an iterative approach:
C++
#include <iostream>
using namespace std;
int fibonacciSearch(int arr[], int n, int x) {
if (n == 0) {
return -1;
}
int fib1 = 0, fib2 = 1, fib3 = fib1 + fib2;
while (fib3 < n) {
fib1 = fib2;
fib2 = fib3;
fib3 = fib1 + fib2;
}
int offset = -1;
while (fib3 > 1) {
int i = min(offset + fib2, n-1);
if (arr[i] < x) {
fib3 = fib2;
fib2 = fib1;
fib1 = fib3 - fib2;
offset = i;
}
else if (arr[i] > x) {
fib3 = fib1;
fib2 = fib2 - fib1;
fib1 = fib3 - fib2;
}
else {
return i;
}
}
if (fib2 == 1 && arr[offset+1] == x) {
return offset + 1;
} else {
return -1;
}
}
int main() {
int arr[] = {10, 22, 35, 40, 45, 50, 80, 82, 85, 90, 100, 235};
int n = sizeof(arr)/sizeof(arr[0]);
int x = 235;
int ind = fibonacciSearch(arr, n, x);
if (ind >= 0) {
cout << "Found at index: " << ind << endl;
} else {
cout << x << " isn't present in the array" << endl;
}
return 0;
}
|
Java
import java.util.*;
class Main {
public static int fibonacciSearch(int[] arr, int x) {
int n = arr.length;
if (n == 0) {
return -1;
}
int fib1 = 0, fib2 = 1, fib3 = fib1 + fib2;
while (fib3 < n) {
fib1 = fib2;
fib2 = fib3;
fib3 = fib1 + fib2;
}
int offset = -1;
while (fib3 > 1) {
int i = Math.min(offset + fib2, n-1);
if (arr[i] < x) {
fib3 = fib2;
fib2 = fib1;
fib1 = fib3 - fib2;
offset = i;
}
else if (arr[i] > x) {
fib3 = fib1;
fib2 = fib2 - fib1;
fib1 = fib3 - fib2;
}
else {
return i;
}
}
if (fib2 == 1 && arr[offset+1] == x) {
return offset + 1;
} else {
return -1;
}
}
public static void main(String[] args) {
int[] arr = {10, 22, 35, 40, 45, 50, 80, 82, 85, 90, 100, 235};
int n = arr.length;
int x = 235;
int ind = fibonacciSearch(arr, x);
if (ind >= 0) {
System.out.println("Found at index: " + ind);
} else {
System.out.println(x + " isn't present in the array");
}
}
}
|
Python3
def fibonacci_search(arr, x):
n = len(arr)
if n == 0:
return -1
fib1, fib2 = 0, 1
fib3 = fib1 + fib2
while fib3 < n:
fib1, fib2 = fib2, fib3
fib3 = fib1 + fib2
offset = -1
while fib3 > 1:
i = min(offset + fib2, n-1)
if arr[i] < x:
fib3 = fib2
fib2 = fib1
fib1 = fib3 - fib2
offset = i
elif arr[i] > x:
fib3 = fib1
fib2 = fib2 - fib1
fib1 = fib3 - fib2
else:
return i
if fib2 == 1 and arr[offset+1] == x:
return offset + 1
else:
return -1
arr = [10, 22, 35, 40, 45, 50,
80, 82, 85, 90, 100,235]
n = len(arr)
x = 235
ind = fibonacci_search(arr, x)
if ind>=0:
print("Found at index:",ind)
else:
print(x,"isn't present in the array");
|
C#
using System;
class GFG {
public static int FibonacciSearch(int[] arr, int x) {
int n = arr.Length;
if (n == 0) {
return -1;
}
int fib1 = 0, fib2 = 1, fib3 = fib1 + fib2;
while (fib3 < n) {
fib1 = fib2;
fib2 = fib3;
fib3 = fib1 + fib2;
}
int offset = -1;
while (fib3 > 1) {
int i = Math.Min(offset + fib2, n - 1);
if (arr[i] < x) {
fib3 = fib2;
fib2 = fib1;
fib1 = fib3 - fib2;
offset = i;
}
else if (arr[i] > x) {
fib3 = fib1;
fib2 = fib2 - fib1;
fib1 = fib3 - fib2;
}
else {
return i;
}
}
if (fib2 == 1 && arr[offset + 1] == x) {
return offset + 1;
} else {
return -1;
}
}
public static void Main(string[] args) {
int[] arr = { 10, 22, 35, 40, 45, 50, 80, 82, 85, 90, 100, 235 };
int n = arr.Length;
int x = 235;
int ind = FibonacciSearch(arr, x);
if (ind >= 0) {
Console.WriteLine("Found at index: " + ind);
} else {
Console.WriteLine(x + " isn't present in the array");
}
}
}
|
Javascript
function fibonacci_search(arr, x) {
var n = arr.length;
if (n === 0) {
return -1;
}
var fib1 = 0;
var fib2 = 1;
var fib3 = fib1 + fib2;
while (fib3 < n) {
fib1 = fib2;
fib2 = fib3;
fib3 = fib1 + fib2;
}
var offset = -1;
while (fib3 > 1) {
var i = Math.min(offset + fib2, n - 1);
if (arr[i] < x) {
fib3 = fib2;
fib2 = fib1;
fib1 = fib3 - fib2;
offset = i;
} else if (arr[i] > x) {
fib3 = fib1;
fib2 = fib2 - fib1;
fib1 = fib3 - fib2;
} else {
return i;
}
}
if (fib2 === 1 && arr[offset + 1] === x) {
return offset + 1;
} else {
return -1;
}
}
var arr = [10, 22, 35, 40, 45, 50,
80, 82, 85, 90, 100,235];
var n = arr.length;
var x = 235;
var ind = fibonacci_search(arr, x);
if (ind >= 0) {
console.log("Found at index:", ind);
} else {
console.log(x,"isn't present in the array");
}
|
Output
Found at index: 11
The time complexity of Fibonacci Search is O(log n), where n is the length of the input array.
This is because at each iteration of the algorithm, the search range is reduced by a factor of approximately 1/?, where ? is the golden ratio (? ? 1.618). The number of iterations required to reduce the search range to a single element is approximately log?(n), where log? denotes the natural logarithm.
Since each iteration of Fibonacci Search requires constant time, the overall time complexity of the algorithm is O(log n). This makes Fibonacci Search a faster algorithm than linear search, but slower than binary search and other logarithmic search algorithms such as interpolation search and exponential search.
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...