Find nth Fibonacci number using Golden ratio
Last Updated :
02 Feb, 2023
Fibonacci series = 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ……..
Different methods to find nth Fibonacci number are already discussed. Another simple way of finding nth Fibonacci number is using golden ratio as Fibonacci numbers maintain approximate golden ratio till infinite.
Golden ratio:
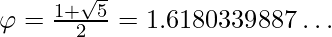
Examples:
Input : n = 9
Output : 34
Input : n = 7
Output : 13
Approach:
Golden ratio may give us incorrect answer.
We can get correct result if we round up the result at each point.
nth fibonacci number = round(n-1th Fibonacci number X golden ratio)
fn = round(fn-1 * 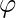 )
)
Till 4th term, the ratio is not much close to golden ratio (as 3/2 = 1.5, 2/1 = 2, …). So, we will consider from 5th term to get next fibonacci number. To find out the 9th fibonacci number f9 (n = 9) :
f6 = round(f5 * 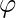 ) = 8 f7 = round(f6 *
) = 8 f7 = round(f6 * 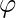 ) = 13 f8 = round(f7 *
) = 13 f8 = round(f7 * 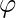 ) = 21 f9 = round(f8 *
) = 21 f9 = round(f8 * 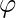 ) = 34
) = 34
Note: This method can calculate first 34 fibonacci numbers correctly. After that there may be difference from the correct value.
Below is the implementation of above approach:
CPP
#include <bits/stdc++.h>
using namespace std;
double PHI = 1.6180339;
int f[6] = { 0, 1, 1, 2, 3, 5 };
int fib(int n)
{
if (n < 6)
return f[n];
int t = 5, fn = 5;
while (t < n) {
fn = round(fn * PHI);
t++;
}
return fn;
}
int main()
{
int n = 9;
cout << n << "th Fibonacci Number = " << fib(n) << endl;
return 0;
}
|
C
#include <math.h>
#include <stdio.h>
double PHI = 1.6180339;
int f[6] = { 0, 1, 1, 2, 3, 5 };
int fib(int n)
{
if (n < 6)
return f[n];
int t = 5, fn = 5;
while (t < n) {
fn = round(fn * PHI);
t++;
}
return fn;
}
int main()
{
int n = 9;
printf("%d th Fibonacci Number = %d\n", n, fib(n));
return 0;
}
|
Java
class GFG
{
static double PHI = 1.6180339;
static int f[] = { 0, 1, 1, 2, 3, 5 };
static int fib (int n)
{
if (n < 6)
return f[n];
int t = 5;
int fn = 5;
while (t < n) {
fn = (int)Math.round(fn * PHI);
t++;
}
return fn;
}
public static void main (String[] args)
{
int n = 9;
System.out.println(n + "th Fibonacci Number = "
+fib(n));
}
}
|
Python3
PHI = 1.6180339
f = [ 0, 1, 1, 2, 3, 5 ]
def fib ( n ):
if n < 6:
return f[n]
t = 5
fn = 5
while t < n:
fn = round(fn * PHI)
t+=1
return fn
n = 9
print(n, "th Fibonacci Number =", fib(n))
|
C#
using System;
class GFG {
static double PHI = 1.6180339;
static int []f = { 0, 1, 1, 2, 3, 5 };
static int fib (int n)
{
if (n < 6)
return f[n];
int t = 5;
int fn = 5;
while (t < n) {
fn = (int)Math.Round(fn * PHI);
t++;
}
return fn;
}
public static void Main ()
{
int n = 9;
Console.WriteLine(n + "th Fibonacci"
+ " Number = " + fib(n));
}
}
|
PHP
<?php
$PHI = 1.6180339;
function fib ($n)
{
global $PHI;
$f = array(0, 1, 1, 2, 3, 5);
if ($n < 6)
return $f[$n];
$t = 5;
$fn = 5;
while ($t < $n)
{
$fn = round($fn * $PHI);
$t++;
}
return $fn;
}
$n = 9;
echo $n, "th Fibonacci Number = ",
fib($n), "\n";
?>
|
Javascript
<script>
let PHI = 1.6180339;
let f = [ 0, 1, 1, 2, 3, 5 ];
function fib (n)
{
if (n < 6)
return f[n];
let t = 5, fn = 5;
while (t < n) {
fn = Math.round(fn * PHI);
t++;
}
return fn;
}
let n = 9;
document.write(n + "th Fibonacci Number = " + fib(n) + "<br>");
</script>
|
Output9th Fibonacci Number = 34
Time complexity: O(n)
Auxiliary space: O(1)
We can optimize above solution work in O(Log n) by using efficient method to compute power.
The above method may not always produce correct results as floating point computations are involved. This is the reason, this method is not used practically even if it can be optimized to work in O(Log n). Please refer below MIT video for more details.
https://www.youtube.com/watch?v=-EQTVuAhSFY
Share your thoughts in the comments
Please Login to comment...