Minimum number of Fibonacci jumps to reach end
Last Updated :
07 Jun, 2021
Given an array of 0s and 1s, If any particular index i has value 1 then it is a safe index and if the value is 0 then it is an unsafe index. A man is standing at index -1(source) can only land on a safe index and he has to reach the Nth index (last position). At each jump, the man can only travel a distance equal to any Fibonacci Number. You have to minimize the number of steps, provided man can jump only in forward direction.
Note: First few Fibonacci numbers are – 0, 1, 1, 2, 3, 5, 8, 13, 21….
Examples:
Input: arr[]= {0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0}
Output: 3
The person will jump from:
1) index -1 to index 4 (a distance of jump = 5)
2) index 4 to index 6 (a distance of jump = 2)
3) index 6 to the destination (a distance of jump = 5)
Input: arr[]= {0, 0}
Output: 1
The person will jump from:
1) index -1 to destination (a distance of jump = 3)
Approach:
- First, we will create an array fib[] for storing fibonacci numbers.
- Then, we will create a DP array and initialize it with INT_MAX and the 0th index DP[0] = 0 and will move in the same way as Coin Change Problem with minimum number of coins.
- The DP definition and recurrence is as followed:
DP[i] = min( DP[i], 1 + DP[i-fib[j]] )
where i is the current index and j denotes
the jth fibonacci number of which the
jump is possible
- Here DP[i] denotes the minimum steps required to reach index i considering all Fibonacci numbers.
Below is the implementation of the approach:
C++
#include <bits/stdc++.h>
using namespace std;
#define MAX 1e9
int minJumps(int arr[], int N)
{
int fib[30];
fib[0] = 0;
fib[1] = 1;
for (int i = 2; i < 30; i++)
fib[i] = fib[i - 1] + fib[i - 2];
int DP[N + 2];
DP[0] = 0;
for (int i = 1; i <= N + 1; i++)
DP[i] = MAX;
for (int i = 1; i <= N + 1; i++) {
for (int j = 1; j < 30; j++) {
if ((arr[i - 1] == 1
|| i == N + 1)
&& i - fib[j] >= 0)
DP[i] = min(DP[i],
1 + DP[i - fib[j]]);
}
}
if (DP[N + 1] != MAX)
return DP[N + 1];
else
return -1;
}
int main()
{
int arr[] = { 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0 };
int n = sizeof(arr) / sizeof(arr[0]);
cout << minJumps(arr, n);
return 0;
}
|
Java
import java.util.*;
import java.lang.*;
class GFG
{
public static int minJumps(int arr[], int N)
{
int MAX = 1000000;
int[] fib = new int[30];
fib[0] = 0;
fib[1] = 1;
for (int i = 2; i < 30; i++)
fib[i] = fib[i - 1] + fib[i - 2];
int[] DP = new int[N + 2];
DP[0] = 0;
for (int i = 1; i <= N + 1; i++)
DP[i] = MAX;
for (int i = 1; i <= N + 1; i++)
{
for (int j = 1; j < 30; j++)
{
if ((i == N + 1 ||
arr[i - 1] == 1) &&
i - fib[j] >= 0)
DP[i] = Math.min(DP[i], 1 +
DP[i - fib[j]]);
}
}
if (DP[N + 1] != MAX)
return DP[N + 1];
else
return -1;
}
public static void main (String[] args)
{
int[] arr = new int[]{ 0, 0, 0, 1, 1, 0,
1, 0, 0, 0, 0 };
int n = 11;
int ans = minJumps(arr, n);
System.out.println(ans);
}
}
|
Python3
MAX = 1e9
def minJumps(arr, N):
fib = [0 for i in range(30)]
fib[0] = 0
fib[1] = 1
for i in range(2, 30):
fib[i] = fib[i - 1] + fib[i - 2]
DP = [0 for i in range(N + 2)]
DP[0] = 0
for i in range(1, N + 2):
DP[i] = MAX
for i in range(1, N + 2):
for j in range(1, 30):
if ((arr[i - 1] == 1 or i == N + 1) and
i - fib[j] >= 0):
DP[i] = min(DP[i], 1 + DP[i - fib[j]])
if (DP[N + 1] != MAX):
return DP[N + 1]
else:
return -1
arr = [0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0]
n = len(arr)
print(minJumps(arr, n - 1))
|
C#
using System;
using System.Collections.Generic;
class GFG
{
public static int minJumps(int []arr, int N)
{
int MAX = 1000000;
int[] fib = new int[30];
fib[0] = 0;
fib[1] = 1;
for (int i = 2; i < 30; i++)
fib[i] = fib[i - 1] + fib[i - 2];
int[] DP = new int[N + 2];
DP[0] = 0;
for (int i = 1; i <= N + 1; i++)
DP[i] = MAX;
for (int i = 1; i <= N + 1; i++)
{
for (int j = 1; j < 30; j++)
{
if ((i == N + 1 ||
arr[i - 1] == 1) &&
i - fib[j] >= 0)
DP[i] = Math.Min(DP[i], 1 +
DP[i - fib[j]]);
}
}
if (DP[N + 1] != MAX)
return DP[N + 1];
else
return -1;
}
public static void Main (String[] args)
{
int[] arr = new int[]{ 0, 0, 0, 1, 1, 0,
1, 0, 0, 0, 0 };
int n = 11;
int ans = minJumps(arr, n);
Console.WriteLine(ans);
}
}
|
Javascript
<script>
const MAX = 1000000000;
function minJumps(arr, N)
{
let fib = new Array(30);
fib[0] = 0;
fib[1] = 1;
for (let i = 2; i < 30; i++)
fib[i] = fib[i - 1] + fib[i - 2];
let DP = new Array(N + 2);
DP[0] = 0;
for (let i = 1; i <= N + 1; i++)
DP[i] = MAX;
for (let i = 1; i <= N + 1; i++) {
for (let j = 1; j < 30; j++) {
if ((arr[i - 1] == 1
|| i == N + 1)
&& i - fib[j] >= 0)
DP[i] = Math.min(DP[i],
1 + DP[i - fib[j]]);
}
}
if (DP[N + 1] != MAX)
return DP[N + 1];
else
return -1;
}
let arr = [ 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0 ];
let n = arr.length;
document.write(minJumps(arr, n));
</script>
|
Time Complexity: 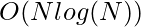
Share your thoughts in the comments
Please Login to comment...