Detect Cycle in Graph using DSU

Given an undirected graph, the task is to check if the graph contains a cycle or not, using DSU.

Examples:

Input: The following is the graph

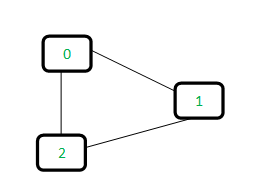
Output: Yes
Explanation: There is a cycle of vertices {0, 1, 2}.

We already have discussed an algorithm to detect cycle in directed graph. Here Union-Find Algorithm can be used to check whether an undirected graph contains cycle or not. The idea is that, 

Initially create subsets containing only a single node which are the parent of itself. Now while traversing through the edges, if the two end nodes of the edge belongs to the same set then they form a cycle. Otherwise, perform union to merge the subsets together.

Note: This method assumes that the graph doesn’t contain any self-loops.

Illustration:

Follow the below illustration for a better understanding

Let us consider the following graph: 

Use an array to keep track of the subsets and which nodes belong to that subset. Let the array be parent[].

Initially, all slots of parent array are initialized to hold the same values as the node.

parent[] = {0, 1, 2}. Also when the value of the node and its parent are same, that is the root of that subset of nodes.

Now process all edges one by one.
Edge 0-1:
        => Find the subsets in which vertices 0 and 1 are. 
        => 0 and 1 belongs to subset 0 and 1.
        => Since they are in different subsets, take the union of them. 
        => For taking the union, either make node 0 as parent of node 1 or vice-versa. 
        => 1 is made parent of 0 (1 is now representative of subset {0, 1})
        => parent[] = {1, 1, 2}

Edge 1-2:
        => 1 is in subset 1 and 2 is in subset 2.
        => Since they are in different subsets, take union.
        => Make 2 as parent of 1. (2 is now representative of subset {0, 1, 2})
        => parent[] = {1, 2, 2}

Edge 0-2:
        => 0 is in subset 2 and 2 is also in subset 2. 
        => Because 1 is parent of 0 and 2 is parent of 1. So 0 also belongs to subset 2
        => Hence, including this edge forms a cycle. 

Therefore, the above graph contains a cycle.

Follow the below steps to implement the idea:

• Initially create a parent[] array to keep track of the subsets.
• Traverse through all the edges:
  • Check to which subset each of the nodes belong to by finding the parent[] array till the node and the parent are the same.
  • If the two nodes belong to the same subset then they belong to a cycle.
  • Otherwise, perform union operation on those two subsets.
• If no cycle is found, return false.

Below is the implementation of the above approach.

C++

// A union-find algorithm to detect cycle in a graph
#include <bits/stdc++.h>
using namespace std;

// a structure to represent an edge in graph
class Edge {
public:
    int src, dest;
};

// a structure to represent a graph
class Graph {
public:
    // V-> Number of vertices, E-> Number of edges
    int V, E;

    // graph is represented as an array of edges
    Edge* edge;
};

// Creates a graph with V vertices and E edges
Graph* createGraph(int V, int E)
{
    Graph* graph = new Graph();
    graph->V = V;
    graph->E = E;

    graph->edge = new Edge[graph->E * sizeof(Edge)];

    return graph;
}

// A utility function to find the subset of an element i
int find(int parent[], int i)
{
    if (parent[i] == i)
        return i;
    return find(parent, parent[i]);
}

// A utility function to do union of two subsets
void Union(int parent[], int x, int y) { parent[x] = y; }

// The main function to check whether a given graph contains
// cycle or not
int isCycle(Graph* graph)
{
    // Allocate memory for creating V subsets
    int* parent = new int[graph->V];

    // Initialize all subsets as single element sets
    for(int i = 0; i < graph->V; i++) {
        parent[i] = i;
    }

    // Iterate through all edges of graph, find subset of
    // both vertices of every edge, if both subsets are
    // same, then there is cycle in graph.
    for (int i = 0; i < graph->E; ++i) {
        int x = find(parent, graph->edge[i].src);
        int y = find(parent, graph->edge[i].dest);

        if (x == y)
            return 1;

        Union(parent, x, y);
    }
    return 0;
}

// Driver code
int main()
{
    /* Let us create the following graph
        0
        | \
        |  \
        1---2 */
    int V = 3, E = 3;
    Graph* graph = createGraph(V, E);

    // add edge 0-1
    graph->edge[0].src = 0;
    graph->edge[0].dest = 1;

    // add edge 1-2
    graph->edge[1].src = 1;
    graph->edge[1].dest = 2;

    // add edge 0-2
    graph->edge[2].src = 0;
    graph->edge[2].dest = 2;

    if (isCycle(graph))
        cout << "Graph contains cycle";
    else
        cout << "Graph doesn't contain cycle";

    return 0;
}

// This code is contributed by rathbhupendra

C

// A union-find algorithm to detect cycle in a graph
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

// a structure to represent an edge in graph
struct Edge {
    int src, dest;
};

// a structure to represent a graph
struct Graph {
    // V-> Number of vertices, E-> Number of edges
    int V, E;

    // graph is represented as an array of edges
    struct Edge* edge;
};

// Creates a graph with V vertices and E edges
struct Graph* createGraph(int V, int E)
{
    struct Graph* graph
        = (struct Graph*)malloc(sizeof(struct Graph));
    graph->V = V;
    graph->E = E;

    graph->edge = (struct Edge*)malloc(
        graph->E * sizeof(struct Edge));

    return graph;
}

// A utility function to find the subset of an element i
int find(int parent[], int i)
{
    if (parent[i] == -1)
        return i;
    return find(parent, parent[i]);
}

// A utility function to do union of two subsets
void Union(int parent[], int x, int y)
{
    parent[y] = x;
}

// The main function to check whether a given graph contains
// cycle or not
int isCycle(struct Graph* graph)
{
    // Allocate memory for creating V subsets
    int* parent = (int*)malloc(graph->V);

    // Initialize all subsets as single element sets
    memset(parent, -1, sizeof(graph->V));

    // Iterate through all edges of graph, find subset of
    // both vertices of every edge, if both subsets are
    // same, then there is cycle in graph.
    for (int i = 0; i < graph->E; ++i) {
        int x = find(parent, graph->edge[i].src);
        int y = find(parent, graph->edge[i].dest);

        if (x == y && (x!=-1 && y!=-1))
            return 1;

        Union(parent, x,y);
    }
    return 0;
}

// Driver program to test above functions
int main()
{
    /* Let us create the following graph
        0
        | \
        |  \
        1---2 */
    int V = 3, E = 3;
    struct Graph* graph = createGraph(V, E);

    // // add edge 0-1
    graph->edge[0].src = 0;
    graph->edge[0].dest = 1;

    // add edge 1-2
    graph->edge[1].src = 1;
    graph->edge[1].dest = 2;

    //add edge 0-2
    graph->edge[2].src = 0;
    graph->edge[2].dest = 2;

    if (isCycle(graph))
        printf("Graph contains cycle");
    else
        printf("Graph doesn't contain cycle");

    return 0;
}

Java

// Java Program for union-find algorithm to detect cycle in
// a graph
import java.io.*;
import java.lang.*;
import java.util.*;

public class Graph {
    int V, E; // V-> no. of vertices & E->no.of edges
    Edge edge[]; // /collection of all edges

    class Edge {
        int src, dest;
    };

    // Creates a graph with V vertices and E edges
    Graph(int v, int e)
    {
        V = v;
        E = e;
        edge = new Edge[E];
        for (int i = 0; i < e; ++i)
            edge[i] = new Edge();
    }

    // A utility function to find the subset of an element i
    int find(int parent[], int i)
    {
        if (parent[i] == i)
            return i;
        return find(parent, parent[i]);
    }

    // A utility function to do union of two subsets
    void Union(int parent[], int x, int y)
    {
        parent[x] = y;
    }

    // The main function to check whether a given graph
    // contains cycle or not
    int isCycle(Graph graph)
    {
        // Allocate memory for creating V subsets
        int parent[] = new int[graph.V];

        // Initialize all subsets as single element sets
        for (int i = 0; i < graph.V; ++i)
            parent[i] = i;

        // Iterate through all edges of graph, find subset
        // of both vertices of every edge, if both subsets
        // are same, then there is cycle in graph.
        for (int i = 0; i < graph.E; ++i) {
            int x = graph.find(parent, graph.edge[i].src);
            int y = graph.find(parent, graph.edge[i].dest);

            if (x == y)
                return 1;

            graph.Union(parent, x, y);
        }
        return 0;
    }

    // Driver Method
    public static void main(String[] args)
    {
        /* Let us create the following graph
        0
        | \
        |  \
        1---2 */
        int V = 3, E = 3;
        Graph graph = new Graph(V, E);

        // add edge 0-1
        graph.edge[0].src = 0;
        graph.edge[0].dest = 1;

        // add edge 1-2
        graph.edge[1].src = 1;
        graph.edge[1].dest = 2;

        // add edge 0-2
        graph.edge[2].src = 0;
        graph.edge[2].dest = 2;

        if (graph.isCycle(graph) == 1)
            System.out.println("Graph contains cycle");
        else
            System.out.println(
                "Graph doesn't contain cycle");
    }
}

Python3

# Python Program for union-find algorithm
# to detect cycle in a undirected graph
# we have one edge for any two vertex
# i.e 1-2 is either 1-2 or 2-1 but not both

from collections import defaultdict

# This class represents a undirected graph
# using adjacency list representation


class Graph:

    def __init__(self, vertices):
        self.V = vertices  # No. of vertices
        self.graph = defaultdict(list)  # default dictionary to store graph

    # function to add an edge to graph
    def addEdge(self, u, v):
        self.graph[u].append(v)

    # A utility function to find the subset of an element i
    def find_parent(self, parent, i):
        if parent[i] == i:
            return i
        if parent[i] != i:
            return self.find_parent(parent, parent[i])

    # A utility function to do union of two subsets
    def union(self, parent, x, y):
        parent[x] = y

    # The main function to check whether a given graph
    # contains cycle or not

    def isCyclic(self):

        # Allocate memory for creating V subsets and
        # Initialize all subsets as single element sets
        parent = [0]*(self.V)
        for i in range(self.V):
            parent[i] = i

        # Iterate through all edges of graph, find subset of both
        # vertices of every edge, if both subsets are same, then
        # there is cycle in graph.
        for i in self.graph:
            for j in self.graph[i]:
                x = self.find_parent(parent, i)
                y = self.find_parent(parent, j)
                if x == y:
                    return True
                self.union(parent, x, y)


# Create a graph given in the above diagram
g = Graph(3)
g.addEdge(0, 1)
g.addEdge(1, 2)
g.addEdge(2, 0)

if g.isCyclic():
    print("Graph contains cycle")
else:
    print("Graph does not contain cycle ")

# This code is contributed by Neelam Yadav

C#

// C# Program for union-find
// algorithm to detect cycle
// in a graph
using System;
class Graph {

    // V-> no. of vertices &
    // E->no.of edges
    public int V, E;

    // collection of all edges
    public Edge[] edge;

    public class Edge {
        public int src, dest;
    };

    // Creates a graph with V
    // vertices and E edges
    public Graph(int v, int e)
    {
        V = v;
        E = e;
        edge = new Edge[E];

        for (int i = 0; i < e; ++i)
            edge[i] = new Edge();
    }

    // A utility function to find
    // the subset of an element i
    int find(int[] parent, int i)
    {
        if (parent[i] == i)
            return i;
        return find(parent, parent[i]);
    }

    // A utility function to do
    // union of two subsets
    void Union(int[] parent, int x, int y)
    {
        parent[x] = y;
    }

    // The main function to check
    // whether a given graph
    // contains cycle or not
    int isCycle(Graph graph)
    {
        // Allocate memory for
        // creating V subsets
        int[] parent = new int[graph.V];

        // Initialize all subsets as
        // single element sets
        for (int i = 0; i < graph.V; ++i)
            parent[i] = i;

        // Iterate through all edges of graph,
        // find subset of both vertices of every
        // edge, if both subsets are same, then
        // there is cycle in graph.
        for (int i = 0; i < graph.E; ++i) {
            int x = graph.find(parent, graph.edge[i].src);
            int y = graph.find(parent, graph.edge[i].dest);

            if (x == y)
                return 1;

            graph.Union(parent, x, y);
        }
        return 0;
    }

    // Driver code
    public static void Main(String[] args)
    {
        /* Let us create the following graph
              0
              | \
              |  \
              1---2 */
        int V = 3, E = 3;
        Graph graph = new Graph(V, E);

        // add edge 0-1
        graph.edge[0].src = 0;
        graph.edge[0].dest = 1;

        // add edge 1-2
        graph.edge[1].src = 1;
        graph.edge[1].dest = 2;

        // add edge 0-2
        graph.edge[2].src = 0;
        graph.edge[2].dest = 2;

        if (graph.isCycle(graph) == 1)
            Console.WriteLine("Graph contains cycle");
        else
            Console.WriteLine(
                "Graph doesn't contain cycle");
    }
}

// This code is contributed by Princi Singh

Javascript

<script>

// Javascript program for union-find
// algorithm to detect cycle
// in a graph

// V-> no. of vertices &
// E->no.of edges
var V, E;

// Collection of all edges
var edge;

class Edge
{
    constructor()
    {
        this.src = 0;
        this.dest = 0;
    }
};

// Creates a graph with V
// vertices and E edges
function initialize(v,e)
{
    V = v;
    E = e;
    edge = Array.from(Array(E), () => Array());
}

// A utility function to find
// the subset of an element i
function find(parent, i)
{
    if (parent[i] == i)
        return i;

    return find(parent, parent[i]);
}

// A utility function to do
// union of two subsets
function Union(parent, x, y)
{
    parent[x] = y;
}

// The main function to check
// whether a given graph
// contains cycle or not
function isCycle()
{

    // Allocate memory for
    // creating V subsets
    var parent = Array(V).fill(0);

    // Initialize all subsets as
    // single element sets
    for(var i = 0; i < V; ++i)
        parent[i] = i;

    // Iterate through all edges of graph,
    // find subset of both vertices of every
    // edge, if both subsets are same, then
    // there is cycle in graph.
    for (var i = 0; i < E; ++i)
    {
        var x = find(parent,
                     edge[i].src);
        var y = find(parent,
                     edge[i].dest);

        if (x == y)
            return 1;

        Union(parent, x, y);
    }
    return 0;
}

// Driver code
/* Let us create the following graph
      0
      | \
      |  \
      1---2 */
var V = 3, E = 3;
initialize(V, E);

// Add edge 0-1
edge[0].src = 0;
edge[0].dest = 1;

// Add edge 1-2
edge[1].src = 1;
edge[1].dest = 2;

// Add edge 0-2
edge[2].src = 0;
edge[2].dest = 2;

if (isCycle() == 1)
    document.write("Graph contains cycle");
else
    document.write("Graph doesn't contain cycle");

// This code is contributed by rutvik_56

</script>

Output

Graph contains cycle

The time and space complexity of the given code is as follows:

Time Complexity:

• Creating the graph takes O(V + E) time, where V is the number of vertices and E is the number of edges.
• Finding the subset of an element takes O(log V) time in the worst case, where V is the number of vertices. The worst case occurs when the tree is skewed, and the depth of the tree is V.
• Union of two subsets takes O(1) time.
• The loop iterating through all edges takes O(E) time.
• Therefore, the overall time complexity of the algorithm is O(E log V).

However, in practice, it can be much faster than O(E log V) because the worst-case scenario of finding the subset of an element does not happen often.

Space Complexity:

• The space complexity of creating the graph is O(E).
• The space complexity of creating the parent array is O(V).
• The space complexity of the algorithm is O(max(V,E)) because at any point in time, there can be at most max(V,E) subsets.
• Therefore, the overall space complexity of the algorithm is O(max(V,E)).