Detect cycle in an undirected graph using BFS
Last Updated :
17 Apr, 2024
Given an undirected graph, how to check if there is a cycle in the graph? For example, the following graph has a cycle of 1-0-2-1.
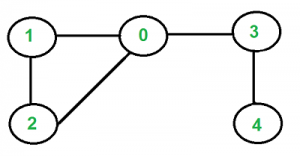
We have discussed cycle detection for the directed graph. We have also discussed a union-find algorithm for cycle detection in undirected graphs.. The time complexity of the union-find algorithm is O(ELogV). Like directed graphs, we can use DFS to detect a cycle in an undirected graph in O(V+E) time. We have discussed DFS based solution for cycle detection in an undirected graph.
In this article, the BFS based solution is discussed. The basic idea is to keep track of visited nodes during BFS traversal. If a node is encountered more than once during BFS, it indicates the presence of a cycle in the graph.
Here are the key steps for detecting cycles:
- Start BFS traversal from each unvisited node in the graph.
- While traversing, mark each visited node.
- If a node is encountered that is already marked as visited, it implies the presence of a cycle.
- Continue BFS traversal until all nodes are visited or a cycle is detected.
Implementation:
C++
// C++ Program to detect cycle in an undirected graph using BFS
#include <bits/stdc++.h>
using namespace std;
void addEdge(vector<int> adj[], int u, int v)
{
adj[u].push_back(v);
adj[v].push_back(u);
}
bool isCyclicConnected(vector<int> adj[], int s, int V, vector<bool>& visited){
// Create a queue for BFS
queue<int> q;
// Enqueue the current node
q.push(s);
while (!q.empty()) {
// Dequeue a vertex from queue and print it
int v = q.front();
q.pop();
if (visited[v] == 1) {
return true; // Cycle detected
}
visited[v] = 1; // Mark as visited
// Visit adjacent nodes
for (auto it : adj[v]) {
if (visited[it] == 0) {
q.push(it);
}
}
}
return false;
}
bool isCyclicDisconnected(vector<int> adj[], int V){
// Mark all the vertices as not visited
vector<bool> visited(V, false);
for (int i = 0; i < V; i++) {
if (!visited[i]
&& isCyclicConnected(adj, i, V, visited))
return true;
}
return false;
}
// Driver program to test methods of graph class
int main(){
int V = 4;
vector<int> adj[V];
addEdge(adj, 0, 1);
addEdge(adj, 1, 2);
addEdge(adj, 2, 0);
addEdge(adj, 2, 3);
if (isCyclicDisconnected(adj, V))
cout << "Yes";
else
cout << "No";
return 0;
}
// This code is contributed by Yash Agarwal(yashagarwal2852002)
import java.util.*;
public class Main {
public static void addEdge(ArrayList<Integer>[] adj, int u, int v) {
adj[u].add(v);
adj[v].add(u);
}
public static boolean isCyclicConnected(ArrayList<Integer>[] adj, int s, int V, boolean[] visited) {
Queue<Integer> q = new LinkedList<>();
q.add(s);
while (!q.isEmpty()) {
int v = q.poll();
if (visited[v]) {
return true; // Cycle detected
}
visited[v] = true; // Mark as visited
for (int it : adj[v]) {
if (!visited[it]) {
q.add(it);
}
}
}
return false;
}
public static boolean isCyclicDisconnected(ArrayList<Integer>[] adj, int V) {
boolean[] visited = new boolean[V];
for (int i = 0; i < V; i++) {
if (!visited[i] && isCyclicConnected(adj, i, V, visited)) {
return true;
}
}
return false;
}
public static void main(String[] args) {
int V = 4;
ArrayList<Integer>[] adj = new ArrayList[V];
for (int i = 0; i < V; i++) {
adj[i] = new ArrayList<>();
}
addEdge(adj, 0, 1);
addEdge(adj, 1, 2);
addEdge(adj, 2, 0);
addEdge(adj, 2, 3);
if (isCyclicDisconnected(adj, V))
System.out.println("Yes");
else
System.out.println("No");
}
}
from collections import deque
def addEdge(adj, u, v):
adj[u].append(v)
adj[v].append(u)
def isCyclicConnected(adj, s, V, visited):
q = deque()
q.append(s)
while q:
v = q.popleft()
if visited[v]:
return True # Cycle detected
visited[v] = True # Mark as visited
for it in adj[v]:
if not visited[it]:
q.append(it)
return False
def isCyclicDisconnected(adj, V):
visited = [False] * V
for i in range(V):
if not visited[i] and isCyclicConnected(adj, i, V, visited):
return True
return False
V = 4
adj = [[] for _ in range(V)]
addEdge(adj, 0, 1)
addEdge(adj, 1, 2)
addEdge(adj, 2, 0)
addEdge(adj, 2, 3)
if isCyclicDisconnected(adj, V):
print("Yes")
else:
print("No")
using System;
using System.Collections.Generic;
class MainClass {
public static void addEdge(List<int>[] adj, int u, int v) {
adj[u].Add(v);
adj[v].Add(u);
}
public static bool isCyclicConnected(List<int>[] adj, int s, int V, bool[] visited) {
Queue<int> q = new Queue<int>();
q.Enqueue(s);
while (q.Count > 0) {
int v = q.Dequeue();
if (visited[v]) {
return true; // Cycle detected
}
visited[v] = true; // Mark as visited
foreach (int it in adj[v]) {
if (!visited[it]) {
q.Enqueue(it);
}
}
}
return false;
}
public static bool isCyclicDisconnected(List<int>[] adj, int V) {
bool[] visited = new bool[V];
for (int i = 0; i < V; i++) {
if (!visited[i] && isCyclicConnected(adj, i, V, visited)) {
return true;
}
}
return false;
}
public static void Main(string[] args) {
int V = 4;
List<int>[] adj = new List<int>[V];
for (int i = 0; i < V; i++) {
adj[i] = new List<int>();
}
addEdge(adj, 0, 1);
addEdge(adj, 1, 2);
addEdge(adj, 2, 0);
addEdge(adj, 2, 3);
if (isCyclicDisconnected(adj, V))
Console.WriteLine("Yes");
else
Console.WriteLine("No");
}
}
function addEdge(adj, u, v) {
adj[u].push(v);
adj[v].push(u);
}
function isCyclicConnected(adj, s, V, visited) {
let q = [];
q.push(s);
while (q.length > 0) {
let v = q.shift();
if (visited[v]) {
return true; // Cycle detected
}
visited[v] = true; // Mark as visited
for (let it of adj[v]) {
if (!visited[it]) {
q.push(it);
}
}
}
return false;
}
function isCyclicDisconnected(adj, V) {
let visited = new Array(V).fill(false);
for (let i = 0; i < V; i++) {
if (!visited[i] && isCyclicConnected(adj, i, V, visited)) {
return true;
}
}
return false;
}
let V = 4;
let adj = [...Array(V)].map(() => []);
addEdge(adj, 0, 1);
addEdge(adj, 1, 2);
addEdge(adj, 2, 0);
addEdge(adj, 2, 3);
if (isCyclicDisconnected(adj, V))
console.log("Yes");
else
console.log("No");
Time Complexity: The program does a simple BFS Traversal of the graph and the graph is represented using an adjacency list. So the time complexity is O(V+E)
Space Complexity: O(V) for visited vector.
Share your thoughts in the comments
Please Login to comment...