Designing Deterministic Finite Automata (Set 1)

Prerequisite – Designing finite automata In this article, we will see some designing of Deterministic Finite Automata (DFA). 

Problem-1: Construction of a DFA for the set of string over {a, b} such that length of the string |w|=2 i.e, length of the string is exactly 2. Explanation – The desired language will be like:

L = {aa, ab, ba, bb} 

The state transition diagram of the language will be like: 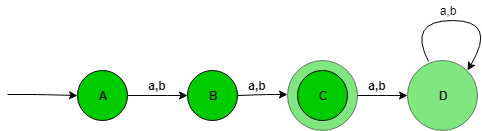Here, State A represent set of all string of length zero (0), state B represent set of all string of length one (1), state C represent set of all string of length two (2). State C is the final state and D is the dead state it is so because after getting any alphabet as input it will not go into final state ever.

Number of states: n+2
Where n is |w|=n 

The above automata will accept all the strings having the length of the string exactly 2. When the length of the string is 1, then it will go from state A to B. When the length of the string is 2, then it will go from state B to C and when the length of the string is greater than 2, then it will go from state C to D (Dead state) and after it from state D TO D itself. 

Python3

#check string in
#in state A
def checkStateA(n):

    #if length of
    #string is one
    #print not accepted
    if(len(n)==1):
        print("string not accepted")
    else:
        #pass string to stateB to
        #to check further transitions
        if(n[0]=='a' or n[0]=='b'):
            stateB(n[1:])


def stateB(n):
    #here if length
    #is not 1 print#string not accepted
    if(len(n)!=1):
        print("string not accepted")
    else:
        #else pass string
        #to state c
        stateC(n[1:])
def stateC(n):
    #here if length
    #becomes zero
    #print accepted
    #else not accepted
    if (len(n)==0):
        print("string accepted")
    else:
        print("string not accepted")


#take input
n=input()
checkStateA(n)

Problem-2: Construction of a DFA for the set of string over {a, b} such that length of the string |w|>=2 i.e, length of the string should be at least 2. Explanation – The desired language will be like:

L = {aa, ab, ba, bb, aaa, aab, aba, abb........} 

The state transition diagram of the language will be like: Here, State A represent set of all string of length zero (0), state B represent set of all string of length one (1), and state C represent set of all string of length two (2).

Number of states: n+1
Where n is |w|>=n 

The above automata will accept all the strings having the length of the string at least 2. When the length of the string is 1, then it will go from state A to B. When the length of the string is 2, then it will go from state B to C and lastly when the length of the string is greater than 2, then it will go from state C to C itself. 

Python3

#check string in
#in state A
def checkStateA(n):

    #if length of
    #string is one
    #print not accepted
    if(len(n)==1):
        print("string not accepted")
    else:
        #pass string to stateB to
        #to check further transitions
        if(n[0]=='a' or n[0]=='b'):
            stateB(n[1:])


def stateB(n):

    #here if length
    #is less than 1
    #printstring not accepted
    if(len(n)<1):
        print("string not accepted")
    else:

        #else pass string
        #to state c
        stateC(n[1:])


def stateC(n):
    #here if length of string
    #is greater than equal to zero
    #print accepted
    #else not accepted
    if (len(n)>=0):
        print("string accepted")
    else:
        print("string not accepted")


#take input
n=input()
checkStateA(n)

Problem-3: Construction of a DFA for the set of string over {a, b} such that length of the string |w|<=2 i.e, length of the string is atmost 2.
Explanation – The desired language will be like:

L = {?, aa, ab, ba, bb} 

The state transition diagram of the language will be like:

Here, State A represent set of all string of length zero (0), state B represent set of all string of length one (1), state C represent set of all string of length two (2), state A, B, C is the final state and D is the dead state it is so because after getting any alphabet as input it will not go into final state ever.

Number of states: n+2
Where n is |w|<=n 

The above automata will accept all the strings having the length of the string at most 2. When the length of the string is 1, then it will go from state A to B. When the length of the string is 2, then it will go from state B to C and lastly when the length of the string is greater than 2, then it will go from state C to D (Dead state). 

Python3

#check string in
#in state A
def checkStateA(n):

    #if only two transition occurs
    #then print string accepted

    if(n[0]=='a' or n[0]=='b'):
        stateB(n[1:])


def stateB(n):

    #if length is 0
    #print accepted
    if(len(n)==0):
        print("string accepted")
    else:
        stateC(n[1:])


def stateC(n):
    #if length is 0
    #print accepted
    #else not accepted
    if (len(n)==0):
        print("string accepted")
    else:
        print("string not accepted")


#take input
n=input()
checkStateA(n)