How to Calculate a Definite Integral?
Last Updated :
30 Aug, 2022
ELet p(x) be the antiderivative of a continuous function f(x) defined on [a, b] then, the definite integral of f(x) over [a, b] is denoted by 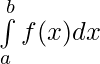 and is equal to [p(b) – p(a)].
and is equal to [p(b) – p(a)].
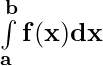 = P(b) – P(a)
= P(b) – P(a)
The numbers a and b are called the limits of integration where a is called the lower limit and b is called the upper limit. The interval [a, b] is called the interval of the integration.
Note
- Constant integration is not included in the evaluation of the definite integral.
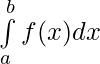 is read as “integral of f(x) from a to b”
is read as “integral of f(x) from a to b”
Steps to find Definite Integrals
To find the definite integral of f(x) over interval [a, b] i.e. 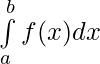 we have following steps:
we have following steps:
- Find the indefinite integral ∫f(x)dx .
- Evaluate P(a) and P(b) where P(x) is antiderivative of f(x), P(a) is value of antiderivative at x=a and P(b) is value of antiderivative at x=b.
- Calculate P(b) – P(a).
- The resultant is the desired value of the definite integral.
Definite Integrals by Substitution
For the integral 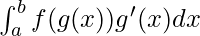 . Let g(x) = t, then g'(x) dx = dt where for x = a , t = g(a) and for x = b, t = g(b).
. Let g(x) = t, then g'(x) dx = dt where for x = a , t = g(a) and for x = b, t = g(b).
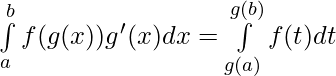
If the variable is changed in the definite integral then substitution of a new variable affects the integrand, the differential (i.e. dx), and the limits.
The limits of the new variable t are the values of t corresponding to the values of the original variable x. It can be obtained by putting values of x in the substitution relation of x and t.
Properties of Definite Integral
Property 1)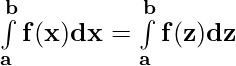
Proof:
Let p(x) be a antiderivative of f(x). Then,
 {p(x)} = f(x) ⇒ \
{p(x)} = f(x) ⇒ \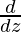 {p(z)} = f(z)
{p(z)} = f(z)
![Rendered by QuickLaTeX.com \int\limits_{a}^b f(x)dx = \big[p(x)\big]_a^b](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d16bd6fb550e935e4d5f94121ace09b0_l3.png) = p(b) – p(a) ——————- (i)
= p(b) – p(a) ——————- (i)
and ![Rendered by QuickLaTeX.com \int\limits_{a}^b f(z)dz = \big[p(z)\big]_a^b](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-33f3928eebb78fdb8366fa85e0329938_l3.png) = p(b) – p(a) ——————-(ii)
= p(b) – p(a) ——————-(ii)
From (i) and (ii)
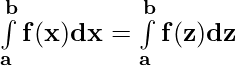
Property 2) 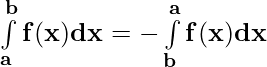
If the limits of the definite integral are interchanged then, its value changes by a minus sign only.
Proof:
Let p(x) be the antiderivative of f(x). Then,
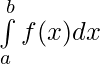 = p(b) – p(a)
= p(b) – p(a)
and 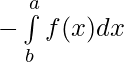 = -[p(a) – p(b)] = p(b) – p(a)
= -[p(a) – p(b)] = p(b) – p(a)
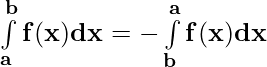
Property 3)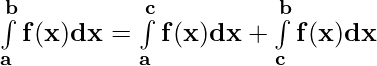 where a < c < b
where a < c < b
Proof:
Let p(x) be the antiderivative of f(x). Then,
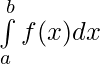 = p(b) – p(a) ——————(i)
= p(b) – p(a) ——————(i)
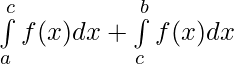 = [p(c) – p(a)] + [p(b) – p(c)] = p(b) – p(a) ——————(ii)
= [p(c) – p(a)] + [p(b) – p(c)] = p(b) – p(a) ——————(ii)
From (i) and (ii)
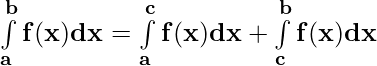
Property 4) 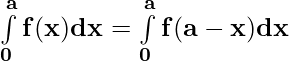
Proof:
Let x = a – t . Then, dx = d(a – t) ⇒ dx = -dt
When x = 0 ⇒ t = a and x = a ⇒ t = 0
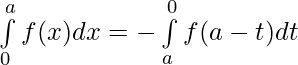
⇒ 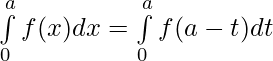 [ By second property ]
[ By second property ]
⇒ 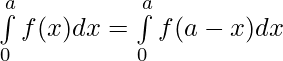 [ By first property ]
[ By first property ]
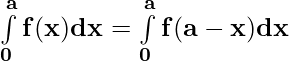
Property 5) 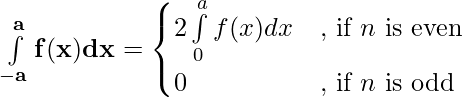
Proof:
Using third property
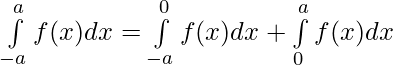 ——————–(i)
——————–(i)
Let x = – t , dx = -dt
Limits : x= -a ⇒ t = a and x = 0 ⇒ t = 0
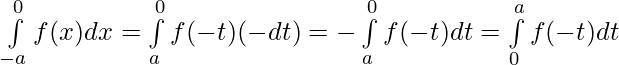 [By second property]
[By second property]
⇒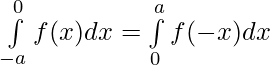 [By first property] ———–(ii)
[By first property] ———–(ii)
From (i) and (ii)
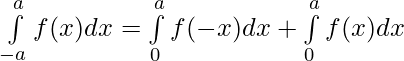
⇒![Rendered by QuickLaTeX.com \int\limits_{-a}^{a}f(x)dx=\int\limits_{0}^{a}[f(-x)+f(x)]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-38c4aa3c932dced55a7e97fb2048cb8a_l3.png)
⇒ 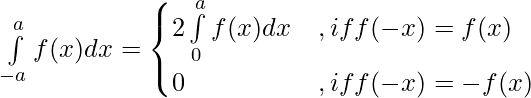
⇒ 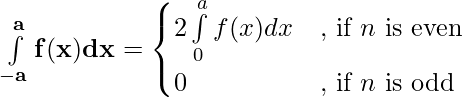
Property 6) If f(x) is a continuous function defined on [0, 2a],
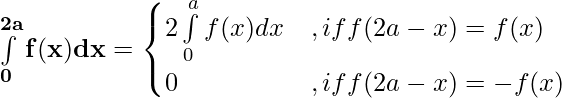
Proof:
Using third property
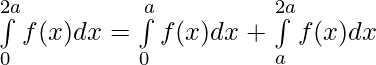 —————–(i)
—————–(i)
Consider 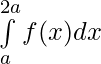
Let x = 2a – t , dx = -d(2a – t) ⇒ dx = -dt
Limits : x= a ⇒ t = a and x = 2a ⇒ t = 0
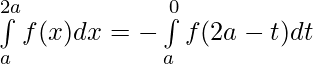
⇒ 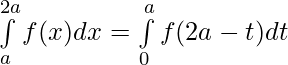 [ Using second property]
[ Using second property]
⇒ 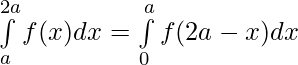 [ Using first property]
[ Using first property]
Substituting 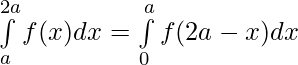 in (i)
in (i)
![Rendered by QuickLaTeX.com \int\limits_{0}^{2a}f(x)dx=\int\limits_{0}^{a}f(x)dx+\int\limits_{0}^{a}f(2a - x)dx = \int\limits_{0}^{a}[f(x) + f(2a - x)]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ac9b1615132b60c21ccdf595faa34f2a_l3.png)
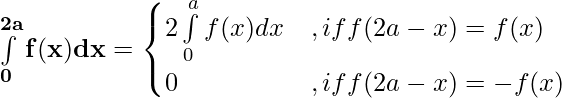
Property 7) 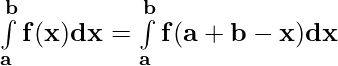
Proof
Let t = a + b – x ⇒ dt = -dx
Limits : x = a , y = b and x = b , y = a
After putting value and limit of t in 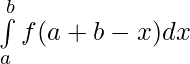
⇒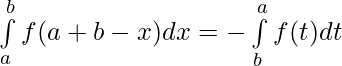
⇒ 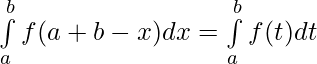 [Using second property]
[Using second property]
⇒ 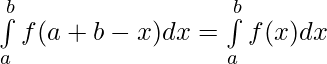 [Using first property]
[Using first property]
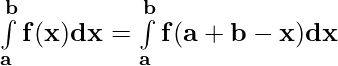
Solved Example on Definite Integrals
Problem 1: Evaluate:
(i) 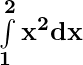
(ii) 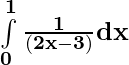
(iii) 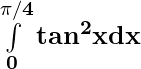
Solution:
(i) 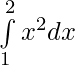 =
= ![Rendered by QuickLaTeX.com \big[x^3\big]_{1}^{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fd3e1bbd6824a8c02184404c3bf6f1ac_l3.png)
= [23 – 13]
= 8 – 1
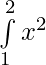 dx = 7
dx = 7
(ii) 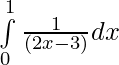 =
= ![Rendered by QuickLaTeX.com \frac{1}{2}\big[log(2x-3)\big]_{0}^{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8457e6c7f9e265c66c95716adba3f1ae_l3.png)
= (1/2)[log|-1| – log|-3| ]
= (1/2)[ log 1 – log 3]
= (1/2)[0 – log 3]
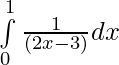 = (1/2)log 3
= (1/2)log 3
(iii) 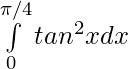 =
= 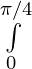 (sec2 x – 1) dx
(sec2 x – 1) dx
= ![Rendered by QuickLaTeX.com \big[tanx - x\big]_{0}^{\pi/4}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-edcebbca2c51c3e1fe4a7858a53dfd80_l3.png)
= [tan(π/4) – (π/4)] – [tan 0 – 0 ]
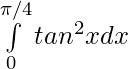 = 1 – (π/4)
= 1 – (π/4)
Problem 2: Evaluate: 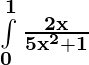
Solution:
Let 5x2 + 1 = t. Then, d(5x2 + 1) = dt ⇒ 10 x dx = dt
For limits : Lower limit ⇒ x = 0 then t = 5x2 +1 = 1 and Upper limit ⇒ x = 1 then t = 5x2 + 1 = 6
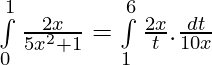
= 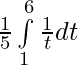
= ![Rendered by QuickLaTeX.com \frac{1}{5}\big[log\hspace{0.1cm}t\big]_1^6](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-095600c8f792450ef6b4c478545b1a42_l3.png)
= (1/5) [log 6 – log 1]
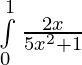 = (1/5) log 6
= (1/5) log 6
Problem 3: Evaluate : 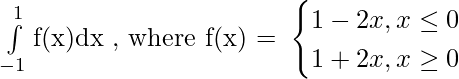
Solution:
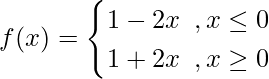
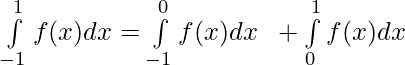
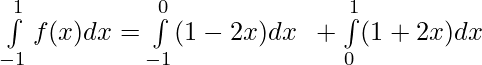 [Using definition of f(x)]
[Using definition of f(x)]
![Rendered by QuickLaTeX.com \int\limits_{-1}^{1} f(x) dx = \big[x-x^2\big]_{-1}^0 \hspace{0.2cm}+ \big[x + x^2\big]_{0}^1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1f69167be35944287458f950f562c149_l3.png)
= [0 – ( -1 – 1)] + [(1 + 1) – (0)]
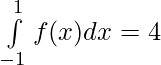
Problem 4: Evaluate: 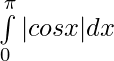
Solution:
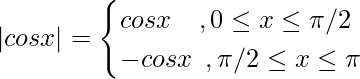
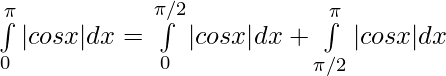
⇒ 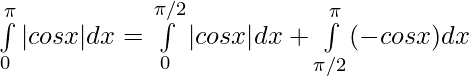
⇒ ![Rendered by QuickLaTeX.com \int\limits_0^\pi|cos x| dx = \big[cos x\big]_0^{\pi/2} - [sin x\big] _{\pi/2}^\pi](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6b0a51637020c20901e20d047a615af7_l3.png)
= 1 + 1
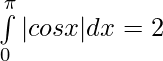
Problems 5: Evaluate: 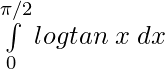
Solution:
I = 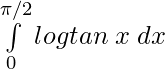 ———————(i)
———————(i)
I = 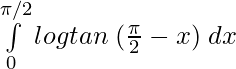
Using 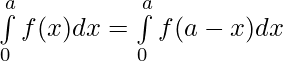
I = 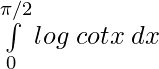 ——————-(ii)
——————-(ii)
Adding (i) and (ii)
2I = ![Rendered by QuickLaTeX.com \int\limits_0^{\pi/2}[log \hspace{0.1cm}tanx\hspace{0.1cm} +log \hspace{0.1cm}cotx\hspace{0.1cm}]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dab7c2b87ed309bb305ccf7a08ea57c4_l3.png)
2I = ![Rendered by QuickLaTeX.com \int\limits_0^{\pi/2}[log \hspace{0.1cm}(tanx\hspace{0.1cm} cotx)\hspace{0.1cm}]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-791ce23884e054b9d9301ddbaad2d641_l3.png)
2I = 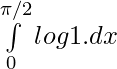
2I = 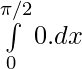
I = 0
Problem 6 : Evaluate : 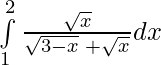
Solution:
I =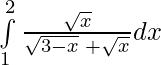 —————–(i)
—————–(i)
Using property 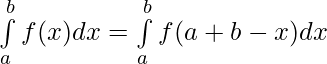
I = 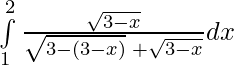
I = 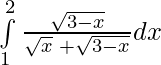 —————(ii)
—————(ii)
Adding (i) and (ii)
2I = 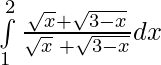
2I = ![Rendered by QuickLaTeX.com \int\limits_1^21.dx =\big[x\big]_1^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-72d41902dd0b3f564c46081cb922a1c7_l3.png)
2I = 2 – 1
2I = 1
I = 1/2
FAQs on Definite Integrals
Question 1: What is meant by definite integrals?
Answer:
Definite integrals are integrals that are defined under proper limits i.e. their upper and lower limits are specified. It is represented as ∫ba f(x) dx where a is the upper limit and b is the lower limit of integration.
Question 2: How are definite integrals simplified?
Answer:
For simplifying definite integrals use the following steps:
- Simplify the integral normally.
- Substitute upper and lower limits to the answer of integration.
- Subtract both the answer obtained in step 2
Question 3: Write the formula for solving definite integrals.
Answer:
Suppose a definite integral of a function f(x) in the interval [a, b] is required, then,
∫ba f(x) dx = F(a) – F(b)
where, ∫ f(x) dx = F(x) + C
Question 4: What does the value obtained from solving definite integral represent? Can it be negative?
Answer:
The value obtained from solving the definite integral represents the area. Yes, it can also be negative.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...