Number of Walks from source to destination
Last Updated :
01 Nov, 2020
Given a graph and two vertices src and dest, count the total number of paths from src to dest where the length of the path is k (there should be exactly k edges between them). Note that the graph is represented as an adjacency matrix.
For example, consider the following graph:

The number of paths from vertex 0 to vertex 3 with length 2 is 2 ({0->1->3} and {0->2->3}).
We have already discussed a O(V3 K) approach in count all possible walks from a source to a destination with exactly k edges. In this post, a O(V3 Log K) approach is discussed.
Approach: The idea is to compute a resultant matrix where result = (graph)k. The total number of paths from source to the destination of length k will then be simply result[src][dest]. We use this technique to compute the exponentiation of the adjacency matrix of the given graph.
The recursion tree of power function used here for exponent = 7 looks like below:

Below is the implementation of the above approach:
Output: Total number of walks: 2
Time Complexity:
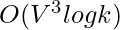
Share your thoughts in the comments
Please Login to comment...