Count of possible hexagonal walks
Last Updated :
27 Jul, 2022
We are given an infinite two dimensional plane made of hexagons connected together. We can visualize this plane as a honeycomb. Element X is present on one of the cells / hexagon.
We are given N steps, the task is to calculate number of such hexagonal paths possible in which element X has to perform a walk of N steps and return back to the original hexagon, where ![Rendered by QuickLaTeX.com N\in[1, 14]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-71fc3cf89db806c8bcd25cba7707903e_l3.png)
Examples:
Input : 1
Output : Number of walks possible is/are 0
Explanation :
0 because using just one step we can move to
any of the adjacent cells but we cannot trace
back to the original hexagon.
Input : 2
Output : Number of walks possible is/are 6
Input : 4
Output : Number of walks possible is/are 90
Approach :
- A hexagonal walk can be defined as walking through adjacent hexagons and returning to the original cell. We know the fact that a hexagon contains six sides i.e. a hexagon is surrounded by six hexagons. Now, we have to count number of ways we take N steps and come back to the original hexagon.
- Now, let us suppose the original hexagon (where element X was initially present) to be the origin. We need all possible ways we can take (N-k) steps such that we have some steps which would trace back to our original hexagon. We can visualize this hexagon and it’s related coordinate system from the picture below.

- Now, let’s assume, our element X was present at 0:0 of the given picture. Thus, we can travel in six possible directions from a hexagon. Now, using the directions above we memorize all possible movements such that we trace back to the original 0:0 index. For memorizing we use a 3D array and we preprocess our answer for a given number of steps and then query accordingly.
Below is the implementation of above approach :
C++
#include <iostream>
using namespace std;
int depth = 16;
int ways[16][16][16];
int stepNum;
void preprocess(int list[])
{
ways[0][8][8] = 1;
for (int N = 1; N <= 14; N++)
{
for (int i = 1; i <= depth; i++)
{
for (int j = 1; j <= depth; j++)
{
ways[N][i][j] = ways[N - 1][i][j + 1]
+ ways[N - 1][i][j - 1]
+ ways[N - 1][i + 1][j]
+ ways[N - 1][i - 1][j]
+ ways[N - 1][i + 1][j - 1]
+ ways[N - 1][i - 1][j + 1];
}
}
list[N] = ways[N][8][8];
}
}
int main()
{
int list[15];
preprocess(list);
int steps = 4;
cout << "Number of walks possible is/are "
<< list[steps] << endl;
return 0;
}
|
Java
import java.util.*;
class GFG {
static int depth = 14;
static int ways[][][] = new int[16][16][16];
static int stepNum;
static void preprocess(int list[])
{
ways[0][8][8] = 1;
for (int N = 1; N <= 14; N++)
{
for (int i = 1; i < depth; i++)
{
for (int j = 1; j < depth; j++)
{
ways[N][i][j] =
ways[N - 1][i][j + 1]
+ ways[N - 1][i][j - 1]
+ ways[N - 1][i + 1][j]
+ ways[N - 1][i - 1][j]
+ ways[N - 1][i + 1][j - 1]
+ ways[N - 1][i - 1][j + 1];
}
}
list[N] = ways[N][8][8];
}
}
public static void main(String[] args)
{
int list[] = new int[15];
preprocess(list);
int steps = 4;
System.out.println( "Number of walks"
+ " possible is/are "+
list[steps] );
}
}
|
Python3
depth = 16
ways = [[[0 for i in range(17)]
for i in range(17)]
for i in range(17)]
def preprocess(list, steps):
ways[0][8][8] = 1
for N in range(1, 16, 1):
for i in range(1, depth, 1):
for j in range(1, depth, 1):
ways[N][i][j] = (ways[N - 1][i][j + 1] +
ways[N - 1][i][j - 1] +
ways[N - 1][i + 1][j] +
ways[N - 1][i - 1][j] +
ways[N - 1][i + 1][j - 1] +
ways[N - 1][i - 1][j + 1])
list[N] = ways[N][8][8]
print("Number of walks possible is/are",
list[steps])
if __name__ == '__main__':
list = [0 for i in range(16)]
steps = 4
preprocess(list, steps)
|
C#
using System;
class GFG {
static int depth = 14;
static int [, ,]ways = new int[16,16,16];
static void preprocess(int []list)
{
ways[0,8,8] = 1;
for (int N = 1; N <= 14; N++)
{
for (int i = 1; i < depth; i++)
{
for (int j = 1; j < depth; j++)
{
ways[N,i,j] =
ways[N - 1,i,j + 1]
+ ways[N - 1,i,j - 1]
+ ways[N - 1,i + 1,j]
+ ways[N - 1,i - 1,j]
+ ways[N - 1,i + 1,j - 1]
+ ways[N - 1,i - 1,j + 1];
}
}
list[N] = ways[N,8,8];
}
}
public static void Main()
{
int []list = new int[15];
preprocess(list);
int steps = 4;
Console.WriteLine( "Number of walks"
+ " possible is/are "+
list[steps] );
}
}
|
Javascript
<script>
let depth = 14;
let ways = new Array(16);
for (let i = 0; i < 16; i++)
{
ways[i] = new Array(16);
for (let j = 0; j < 16; j++)
{
ways[i][j] = new Array(16);
for (let k = 0; k < 16; k++)
{
ways[i][j][k] = 0;
}
}
}
let stepNum;
function preprocess(list)
{
ways[0][8][8] = 1;
for (let N = 1; N <= 14; N++)
{
for (let i = 1; i < depth; i++)
{
for (let j = 1; j < depth; j++)
{
ways[N][i][j] =
ways[N - 1][i][j + 1]
+ ways[N - 1][i][j - 1]
+ ways[N - 1][i + 1][j]
+ ways[N - 1][i - 1][j]
+ ways[N - 1][i + 1][j - 1]
+ ways[N - 1][i - 1][j + 1];
}
}
list[N] = ways[N][8][8];
}
}
let list = new Array(15);
list.fill(0);
preprocess(list);
let steps = 4;
document.write( "Number of walks"
+ " possible is/are "+
list[steps] );
</script>
|
OutputNumber of walks possible is/are 90
The time complexity of the above code is 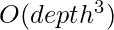 and the space complexity is also similar due to the 3D array used.
and the space complexity is also similar due to the 3D array used.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...