Count all possible walks from a source to a destination with exactly k edges

Given a directed graph and two vertices ‘u’ and ‘v’ in it, count all possible walks from ‘u’ to ‘v’ with exactly k edges on the walk. 

The graph is given adjacency matrix representation where the value of graph[i][j] as 1 indicates that there is an edge from vertex i to vertex j and a value 0 indicates no edge from i to j.

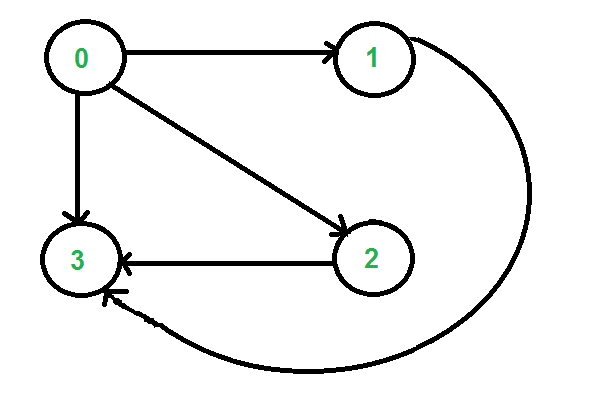
For example, consider the following graph. Let source ‘u’ be vertex 0, destination ‘v’ be 3 and k be 2. The output should be 2 as there are two walks from 0 to 3 with exactly 2 edges. The walks are {0, 2, 3} and {0, 1, 3}

Simple Approach: Create a recursive function that takes the current vertex, destination vertex, and the count of the vertex. Call the recursive function with all adjacent vertices of a current vertex with the value of k as k-1. When the value of k is 0, then check whether the current vertex is the destination or not. If destination, then the output answer is 1.

The following is the implementation of this simple solution.  

C++

// C++ program to count walks from u to
// v with exactly k edges
#include <iostream>
using namespace std;

// Number of vertices in the graph
#define V 4

// A naive recursive function to count
// walks from u to v with k edges
int countwalks(int graph[][V], int u, int v, int k)
{
    // Base cases
    if (k == 0 && u == v)
        return 1;
    if (k == 1 && graph[u][v])
        return 1;
    if (k <= 0)
        return 0;

    // Initialize result
    int count = 0;

    // Go to all adjacents of u and recur
    for (int i = 0; i < V; i++)
        if (graph[u][i] == 1) // Check if is adjacent of u
            count += countwalks(graph, i, v, k - 1);

    return count;
}

// driver program to test above function
int main()
{
    /* Let us create the graph shown in above diagram*/
    int graph[V][V] = { { 0, 1, 1, 1 },
                        { 0, 0, 0, 1 },
                        { 0, 0, 0, 1 },
                        { 0, 0, 0, 0 } };
    int u = 0, v = 3, k = 2;
    cout << countwalks(graph, u, v, k);
    return 0;
}

Java

// Java program to count walks from u to v with exactly k edges
import java.util.*;
import java.lang.*;
import java.io.*;

class KPaths {
    static final int V = 4; // Number of vertices

    // A naive recursive function to count walks from u
    // to v with k edges
    int countwalks(int graph[][], int u, int v, int k)
    {
        // Base cases
        if (k == 0 && u == v)
            return 1;
        if (k == 1 && graph[u][v] == 1)
            return 1;
        if (k <= 0)
            return 0;

        // Initialize result
        int count = 0;

        // Go to all adjacents of u and recur
        for (int i = 0; i < V; i++)
            if (graph[u][i] == 1) // Check if is adjacent of u
                count += countwalks(graph, i, v, k - 1);

        return count;
    }

    // Driver method
    public static void main(String[] args) throws java.lang.Exception
    {
        /* Let us create the graph shown in above diagram*/
        int graph[][] = new int[][] { { 0, 1, 1, 1 },
                                      { 0, 0, 0, 1 },
                                      { 0, 0, 0, 1 },
                                      { 0, 0, 0, 0 } };
        int u = 0, v = 3, k = 2;
        KPaths p = new KPaths();
        System.out.println(p.countwalks(graph, u, v, k));
    }
} // Contributed by Aakash Hasija

Python3

# Python3 program to count walks from
# u to v with exactly k edges

# Number of vertices in the graph
V = 4

# A naive recursive function to count
# walks from u to v with k edges
def countwalks(graph, u, v, k):

    # Base cases
    if (k == 0 and u == v):
        return 1
    if (k == 1 and graph[u][v]):
        return 1
    if (k <= 0):
        return 0

    # Initialize result
    count = 0

    # Go to all adjacents of u and recur
    for i in range(0, V):

        # Check if is adjacent of u
        if (graph[u][i] == 1):
            count += countwalks(graph, i, v, k-1)

    return count

# Driver Code

# Let us create the graph shown in above diagram
graph = [[0, 1, 1, 1, ],
         [0, 0, 0, 1, ],
         [0, 0, 0, 1, ],
         [0, 0, 0, 0] ]

u = 0; v = 3; k = 2
print(countwalks(graph, u, v, k))

# This code is contributed by Smitha Dinesh Semwal.

C#

// C# program to count walks from u to
// v with exactly k edges
using System;

class GFG {

    // Number of vertices
    static int V = 4;

    // A naive recursive function to
    // count walks from u to v with
    // k edges
    static int countwalks(int[, ] graph, int u,
                          int v, int k)
    {

        // Base cases
        if (k == 0 && u == v)
            return 1;
        if (k == 1 && graph[u, v] == 1)
            return 1;
        if (k <= 0)
            return 0;

        // Initialize result
        int count = 0;

        // Go to all adjacents of u and recur
        for (int i = 0; i < V; i++)

            // Check if is adjacent of u
            if (graph[u, i] == 1)
                count += countwalks(graph, i, v, k - 1);

        return count;
    }

    // Driver method
    public static void Main()
    {

        /* Let us create the graph shown
        in above diagram*/
        int[, ] graph = new int[, ] { { 0, 1, 1, 1 },
                                      { 0, 0, 0, 1 },
                                      { 0, 0, 0, 1 },
                                      { 0, 0, 0, 0 } };

        int u = 0, v = 3, k = 2;

        Console.Write(
            countwalks(graph, u, v, k));
    }
}

// This code is contributed by nitin mittal.

PHP

<?php
// PHP program to count walks from u
// to v with exactly k edges

// Number of vertices in the graph
$V = 4;

// A naive recursive function to count
// walks from u to v with k edges
function countwalks( $graph, $u, $v, $k)
{
    global $V;

    // Base cases
    if ($k == 0 and $u == $v)
        return 1;
    if ($k == 1 and $graph[$u][$v])
        return 1;
    if ($k <= 0)
        return 0;

    // Initialize result
    $count = 0;

    // Go to all adjacents of u and recur
    for ( $i = 0; $i < $V; $i++)

        // Check if is adjacent of u
        if ($graph[$u][$i] == 1)
            $count += countwalks($graph, $i,
                                $v, $k - 1);

    return $count;
}

    // Driver Code
    /* Let us create the graph
       shown in above diagram*/
    $graph = array(array(0, 1, 1, 1),
                   array(0, 0, 0, 1),
                   array(0, 0, 0, 1),
                   array(0, 0, 0, 0));
    $u = 0; $v = 3; $k = 2;
    echo countwalks($graph, $u, $v, $k);

// This code is contributed by anuj_67.
?>

Javascript

<script>
// Javascript program to count walks from u to
// v with exactly k edges

// Number of vertices in the graph
var V = 4

// A naive recursive function to count
// walks from u to v with k edges
function countwalks(graph, u, v, k)
{
    // Base cases
    if (k == 0 && u == v)
        return 1;
    if (k == 1 && graph[u][v])
        return 1;
    if (k <= 0)
        return 0;

    // Initialize result
    var count = 0;

    // Go to all adjacents of u and recur
    for (var i = 0; i < V; i++)
        if (graph[u][i] == 1) // Check if is adjacent of u
            count += countwalks(graph, i, v, k - 1);

    return count;
}

// driver program to test above function
/* Let us create the graph shown in above diagram*/
var graph = [[0, 1, 1, 1, ],
         [0, 0, 0, 1, ],
         [0, 0, 0, 1, ],
         [0, 0, 0, 0] ];
var u = 0, v = 3, k = 2;
document.write(countwalks(graph, u, v, k));
// This code contributed by shubhamsingh10
</script>

Output

2

Complexity Analysis:

• Time Complexity: O(V^k). 
  The worst-case time complexity of the above function is O(V^k) where V is the number of vertices in the given graph. We can simply analyze the time complexity by drawing a recursion tree. The worst occurs for a complete graph. In the worst case, every internal node of the recursion tree would have exactly n children.
• Auxiliary Space: O(V). 
  To store the stack space and the visited array O(V) space is needed.

Efficient Approach: The solution can be optimized using Dynamic Programming. The idea is to build a 3D table where the first dimension is the source, the second dimension is the destination, the third dimension is the number of edges from source to destination, and the value is the count of walks. Like others, Dynamic Programming problems, fill the 3D table in a bottom-up manner. 

C++

// C++ program to count walks from
// u to v with exactly k edges
#include <iostream>
using namespace std;

// Number of vertices in the graph
#define V 4

// A Dynamic programming based function to count walks from u
// to v with k edges
int countwalks(int graph[][V], int u, int v, int k)
{
    // Table to be filled up using DP.
    // The value count[i][j][e] will
    // store count of possible walks from
    // i to j with exactly k edges
    int count[V][V][k + 1];

    // Loop for number of edges from 0 to k
    for (int e = 0; e <= k; e++) {
        for (int i = 0; i < V; i++) // for source
        {
            for (int j = 0; j < V; j++) // for destination
            {
                // initialize value
                count[i][j][e] = 0;

                // from base cases
                if (e == 0 && i == j)
                    count[i][j][e] = 1;
                if (e == 1 && graph[i][j])
                    count[i][j][e] = 1;

                // go to adjacent only when the
                // number of edges is more than 1
                if (e > 1) {
                    for (int a = 0; a < V; a++) // adjacent of source i
                        if (graph[i][a])
                            count[i][j][e] += count[a][j][e - 1];
                }
            }
        }
    }
    return count[u][v][k];
}

// driver program to test above function
int main()
{
    /* Let us create the graph shown in above diagram*/
    int graph[V][V] = { { 0, 1, 1, 1 },
                        { 0, 0, 0, 1 },
                        { 0, 0, 0, 1 },
                        { 0, 0, 0, 0 } };
    int u = 0, v = 3, k = 2;
    cout << countwalks(graph, u, v, k);
    return 0;
}

Java

// Java program to count walks from
// u to v with exactly k edges
import java.util.*;
import java.lang.*;
import java.io.*;

class KPaths {
    static final int V = 4; // Number of vertices

    // A Dynamic programming based function to count walks from u
    // to v with k edges
    int countwalks(int graph[][], int u, int v, int k)
    {
        // Table to be filled up using DP. The value count[i][j][e]
        // will/ store count of possible walks from i to j with
        // exactly k edges
        int count[][][] = new int[V][V][k + 1];

        // Loop for number of edges from 0 to k
        for (int e = 0; e <= k; e++) {
            for (int i = 0; i < V; i++) // for source
            {
                for (int j = 0; j < V; j++) // for destination
                {
                    // initialize value
                    count[i][j][e] = 0;

                    // from base cases
                    if (e == 0 && i == j)
                        count[i][j][e] = 1;
                    if (e == 1 && graph[i][j] != 0)
                        count[i][j][e] = 1;

                    // go to adjacent only when number of edges
                    // is more than 1
                    if (e > 1) {
                        for (int a = 0; a < V; a++) // adjacent of i
                            if (graph[i][a] != 0)
                                count[i][j][e] += count[a][j][e - 1];
                    }
                }
            }
        }
        return count[u][v][k];
    }

    // Driver method
    public static void main(String[] args) throws java.lang.Exception
    {
        /* Let us create the graph shown in above diagram*/
        int graph[][] = new int[][] { { 0, 1, 1, 1 },
                                      { 0, 0, 0, 1 },
                                      { 0, 0, 0, 1 },
                                      { 0, 0, 0, 0 } };
        int u = 0, v = 3, k = 2;
        KPaths p = new KPaths();
        System.out.println(p.countwalks(graph, u, v, k));
    }
} // Contributed by Aakash Hasija

Python3

# Python3 program to count walks from
# u to v with exactly k edges

# Number of vertices
V = 4

# A Dynamic programming based function
# to count walks from u to v with k edges


def countwalks(graph, u, v, k):

    # Table to be filled up using DP.
    # The value count[i][j][e] will/
    # store count of possible walks
    # from i to j with exactly k edges
    count = [[[0 for k in range(k + 1)]
              for i in range(V)]
             for j in range(V)]

    # Loop for number of edges from 0 to k
    for e in range(0, k + 1):
        # For Source
        for i in range(V):
            # For Destination
            for j in range(V):
                # Initialize value
                # count[i][j][e] = 0

                # From base cases
                if (e == 0 and i == j):
                    count[i][j][e] = 1
                if (e == 1 and graph[i][j] != 0):
                    count[i][j][e] = 1

                # Go to adjacent only when number
                # of edges is more than 1
                if (e > 1):

                    for a in range(V):

                        # Adjacent of i
                        if (graph[i][a] != 0):
                            count[i][j][e] += count[a][j][e - 1]

    return count[u][v][k]


# Driver code
if __name__ == '__main__':

    # Let us create the graph shown
    # in above diagram
    graph = [[0, 1, 1, 1],
             [0, 0, 0, 1],
             [0, 0, 0, 1],
             [0, 0, 0, 0]]

    u = 0
    v = 3
    k = 2

    print(countwalks(graph, u, v, k))

# This code is contributed by Rajput-Ji

C#

// C# program to count walks from u to v
// with exactly k edges
using System;

class GFG {
    static int V = 4; // Number of vertices

    // A Dynamic programming based function
    // to count walks from u to v with k edges
    static int countwalks(int[, ] graph, int u,
                          int v, int k)
    {
        // Table to be filled up using DP. The
        // value count[i][j][e] will/ store
        // count of possible walks from i to
        // j with exactly k edges
        int[,, ] count = new int[V, V, k + 1];

        // Loop for number of edges from 0 to k
        for (int e = 0; e <= k; e++) {

            // for source
            for (int i = 0; i < V; i++) {

                // for destination
                for (int j = 0; j < V; j++) {
                    // initialize value
                    count[i, j, e] = 0;

                    // from base cases
                    if (e == 0 && i == j)
                        count[i, j, e] = 1;
                    if (e == 1 && graph[i, j] != 0)
                        count[i, j, e] = 1;

                    // go to adjacent only when
                    // number of edges
                    // is more than 1
                    if (e > 1) {
                        // adjacent of i
                        for (int a = 0; a < V; a++)
                            if (graph[i, a] != 0)
                                count[i, j, e] += count[a, j, e - 1];
                    }
                }
            }
        }

        return count[u, v, k];
    }

    // Driver method
    public static void Main()
    {
        /* Let us create the graph shown in
        above diagram*/
        int[, ] graph = { { 0, 1, 1, 1 },
                          { 0, 0, 0, 1 },
                          { 0, 0, 0, 1 },
                          { 0, 0, 0, 0 } };
        int u = 0, v = 3, k = 2;

        Console.WriteLine(
            countwalks(graph, u, v, k));
    }
}

// This is Code Contributed by anuj_67.

Javascript

<script>

// Javascript program to count walks from
// u to v with exactly k edges

// Number of vertices in the graph
var V = 4

// A Dynamic programming based function to count walks from u
// to v with k edges
function countwalks(graph, u, v, k)
{
    // Table to be filled up using DP.
    // The value count[i][j][e] will
    // store count of possible walks from
    // i to j with exactly k edges
    var count = new Array(V);
    for (var i = 0; i <V; i++) {
        count[i] = new Array(V);
        for (var j = 0; j < V; j++) {
            count[i][j] = new Array(V);
            for (var e = 0; e <= k; e++) {
                count[i][j][e] = 0;
            }
        }
    }

    // Loop for number of edges from 0 to k
    for (var e = 0; e <= k; e++) {
        for (var i = 0; i < V; i++) // for source
        {
            for (var j = 0; j < V; j++) // for destination
            {
                // initialize value
                count[i][j][e] = 0;

                // from base cases
                if (e == 0 && i == j)
                    count[i][j][e] = 1;
                if (e == 1 && graph[i][j])
                    count[i][j][e] = 1;

                // go to adjacent only when the
                // number of edges is more than 1
                if (e > 1) {
                    for (var a = 0; a < V; a++) // adjacent of source i
                        if (graph[i][a])
                            count[i][j][e] += count[a][j][e - 1];
                }
            }
        }
    }
    return count[u][v][k];
}

// driver program to test above function
/* Let us create the graph shown in above diagram*/
var graph = [ [ 0, 1, 1, 1 ],
              [ 0, 0, 0, 1 ],
              [ 0, 0, 0, 1 ],
              [ 0, 0, 0, 0 ] ];
var u = 0, v = 3, k = 2;
document.write(countwalks(graph, u, v, k));

// This code is contributed by ShubhamSingh10
</script>

PHP

<?php
// PHP program to count walks from
// u to v with exactly k edges

// Number of vertices in the graph
define('V', 4);

// A Dynamic programming based function to count walks from u
// to v with k edges
function countwalks($graph, $u, $v, $k)
{
    // Table to be filled up using DP.
    // The value count[i][j][e] will
    // store count of possible walks from
    // i to j with exactly k edges
    $count = array();
    for ($i = 0; $i < V; $i++) {
        for ($j = 0; $j < V; $j++) {
            for ($e = 0; $e <= $k; $e++) {
                $count[$i][$j][$e] = 0;
            }
        }
    }

    // Loop for number of edges from 0 to k
    for ($e = 0; $e <= $k; $e++) {
        for ($i = 0; $i < V; $i++) // for source
        {
            for ($j = 0; $j < V; $j++) // for destination
            {
                // initialize value
                $count[$i][$j][$e] = 0;

                // from base cases
                if ($e == 0 && $i == $j)
                    $count[$i][$j][$e] = 1;
                if ($e == 1 && $graph[$i][$j])
                    $count[$i][$j][$e] = 1;

                // go to adjacent only when the
                // number of edges is more than 1
                if ($e > 1) {
                    for ($a = 0; $a < V; $a++) // adjacent of source i
                        if ($graph[$i][$a])
                            $count[$i][$j][$e] += $count[$a][$j][$e - 1];
                }
            }
        }
    }
    return $count[$u][$v][$k];
}

// driver program to test above function
/* Let us create the graph shown in above diagram*/
$graph = array(array(0, 1, 1, 1),
                array(0, 0, 0, 1),
                array(0, 0, 0, 1),
                array(0, 0, 0, 0));

$u = 0;
$v = 3;
$k = 2;
echo countwalks($graph, $u, $v, $k);

// This code is contributed by rajsanghavi9.
?>

Output

2

Complexity Analysis:

• Time Complexity: O(V³). 
  Three nested loops are needed to fill the DP table, so the time complexity is O(V³).
• Auxiliary Space: O(V²K). 
  To store the DP table O(V²K) space is needed.

We can also use Divide and Conquer to solve the above problem in O(V³Logk) time. The count of walks of length k from u to v is the [u][v]’th entry in (graph[V][V])^k. We can calculate the power by doing O(Logk) multiplication by using the divide and conquer technique to calculate power. A multiplication between two matrices of size V x V takes O(V³) time.