Class 10 RD Sharma Solutions- Chapter 1 Real Numbers – Exercise 1.6

Question 1. Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion.

(i)23/8 

Solution:

Denominator = 8 

⇒ 8 = 2³ x 5

The denominator 8 of the fraction 23/8 is of the form 2^m x 5ⁿ, where m, n are non-negative integers.

Therefore, 23/8 has terminating decimal expansion which terminates after three places of decimal.

(ii) 125/441

Solution:

Denominator = 441.

⇒ 441 = 3² x 7²

The denominator 441 of 125/441 is not of the form 2^m x 5ⁿ, where m, n are non-negative integers.

Therefore, the fraction 125/441 has a non-terminating repeating decimal expansion.

(iii) 35/50

Solution:

Denominator = 50.

⇒ 50 = 2 x 5²

The denominator 50 of the fraction 35/50 is of the form 2^m x 5ⁿ, where m, n are non-negative integers.

Therefore, 35/50 has a terminating decimal expansion which terminates after two places of decimal.

(iv) 77/210

Solution:

Denominator = 210.

⇒ 210 = 2 x 3 x 5 x 7

The denominator 210 of the fraction 77/210 is not of the form 2^m x 5ⁿ, where m, n are non-negative integers.

Therefore, 77/210 has non-terminating repeating decimal expansion.

(v) 129/(2² x 5⁷ x 7¹⁷)

Solution:

The denominator = 2² x 5⁷ x 7¹⁷.

The denominator of the fraction cannot be expressed in the form 2^m x 5ⁿ, where m, n are non-negative integers.

Therefore, 125/441 has a non-terminating repeating decimal expansion.

(vi) 987/10500

Solution:

On reducing the above fraction, we have,

987/10500 = 47/500 (reduced form)

Denominator = 500.

⇒ 500 = 2² x 5³

The denominator 500 of 47/500 can be expressed in the form 2^m x 5ⁿ, where m, n are non-negative integers.

Therefore, 987/10500 has a terminating decimal expansion which terminates after three places of decimal.

Question 2. Write down the decimal expansions of the following rational numbers by writing their denominators in the form of 2m x 5n, where m, and n, are the non- negative integers.

(i) 3/8

Solution:

Rational number is 3/8.

We can see that 8 = 2³ is of the form 2^m x 5ⁿ, where m = 3 and n = 0.

Therefore, the given number has terminating decimal expansion.

(ii) 13/125

Solution:

We can see that  125 = 5³ is of the form 2^m x 5ⁿ, where m = 0 and n = 3.

Therefore, the given rational number has terminating decimal expansion.

∴ 13/ 125 = (13 x 2³)/(125 x 2³) 

= 104/1000 

= 0.104

(iii) 7/80

Solution:

We can see, 80 = 2⁴ x 5 is of the form 2^m x 5ⁿ, where m = 4 and n = 1.

Therefore, the given number has terminating decimal expansion.

∴ 7/ 80 = (7 x 5³)/ (2⁴ x 5  x 5³)

 = 7 x  125 / (5 x  2)⁴

= 875/10000 

= 0.0875

(iv) 14588/625

Solution:

We can see, 625 = 5⁴ is of the form 2^m x 5ⁿ where m = 0 and n = 4.

So, the given number has terminating decimal expansion.

∴ 14588/ 625 = (14588 x 2⁴)/ (2⁴ x 5⁴ ) = 233408/10⁴ 

= 233408/10000 = 23.3408

(v) 129/(2² x 5⁷)

Solution:

We can see, 2² x 5⁷ is of the form 2^m x 5ⁿ, where m = 2 and n = 7.

So, the given number has terminating decimal expansion.

∴ 129/ 2² x 5⁷ = 129 x 2⁵ / 2² x 5⁷ x 2⁵

= 4182/10⁷

=4182/10000000

=0.0004182

Question 3. Write the denominator of the rational number 257/5000 in the form 2m × 5n, where m, n are non-negative integers. Hence, write the decimal expansion, without actual division.

Solution:

Denominator = 5000.

⇒ 5000 = 2³ x 5⁴

It’s seen that, 2³ x 5⁴ is of the form 2^m x 5ⁿ, where m = 3 and n = 4.

∴ 257/5000 = (257 x 2)/(5000 x 2) = 514/10000 = 0.0514 is the required decimal expansion.

Question 4. What can you say about the prime factorisation of the denominators of the following rational:

(i) 43.123456789

Solution:

The number 43.123456789 has a terminating decimal expansion. Therefore, its denominator is of the form 2^m x 5ⁿ, where m, n are non-negative integers.

(ii) 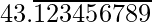[Tex] [/Tex]

Solution:

The given rational has a non-terminating decimal expansion. Therefore, the denominator of the number has factors other than the numbers 2 or 5.

(iii) 27.\overline{142857}

*** QuickLaTeX cannot compile formula:
 

*** Error message:
Error: Nothing to show, formula is empty

Solution:

The given rational number has a non-terminating decimal expansion. Therefore, the denominator of the number has factors other than 2 or 5.

(iv) 0.120120012000120000….

Solution:

Since 0.120120012000120000…. has a non-terminating decimal expansion. Therefore, the denominator of the number has factors other than 2 or 5.

My Personal Notes arrow_drop_up

Save