Question 21. Find the ratio in which the point P(-1, y) lying on the line segment joining A(-3, 10) and B(6, -8) divides it. Also, find the value of y.
Solution:
Assume P divide A(-3, 10) and B(6, -8) in the ratio of k : 1
Given: coordinates of P as (-1, y)
After applying the section formula for x – coordinate,
We will get
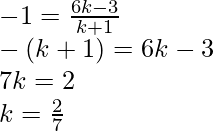
Therefore,
AB is divided by point P in the ratio of 2 : 7
By applying the value of k, to find the y-coordinate
We will get
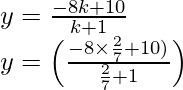
y = (-16 + 70)/(2 + 7) = 54/9
y = 6
Hence,
The y-coordinate of P is 6.
Question 22. Find the coordinates of a point A, where AB is the diameter of circle whose center is (2, -3) and B is (1, 4).
Solution:
Assume the coordinates of point A be (x, y)
Given: AB is the diameter,
So the center in the mid-point of the diameter
Thus,
(2, -3) = (x + 1/ 2, y + 4/2)
2 = x + 1/2 and -3 = y + 4/2
4 = x + 1 and -6 = y + 4
x = 3 and y = -10
Hence, the coordinates of A are (3, -10)
Question 23. If the points (-2, 1), (1, 0), (x, 3), and (1, y) form a parallelogram, find the values of x and y.
Solution:
Consider A(-2, 1), B(1, 0), C(x , 3) and D(1, y) are the given points of the parallelogram.
As we know that the diagonals of a parallelogram bisect each other.
Thus,
Coordinates of mid-point of AC = Coordinates of mid-point of BD
((x – 2)/2, (3 – 1)/2) = (1+1)/2, (y + 0)/2
((x – 2)/2, 1) = (1, y/2)
(x – 2)/2 = 1
x – 2 = 2
x = 4
and y/2 = 1
y = 2
Hence, the value of x is 4 and the value of y is 2.
Question 24. The points A(2, 0), B(9, 1), C(11, 6), and D(4, 4) are the vertices of a quadrilateral ABCD. Determine whether ABCD is a rhombus or not.
Solution:
Given: A(2, 0), B(9, 1), C(11, 6) and D(4, 4).
Mid-point of AC coordinates are 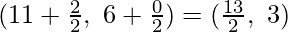
Mid-point of BD coordinates are 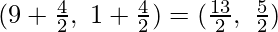
Here,
Coordinates of the mid-point of AC ≠ Coordinates of mid-point of BD,
ABCD is not a parallelogram.
Hence,
ABCD cannot be a rhombus too.
Question 25. In what ratio does the point (-4,6) divide the line segment joining the points A(-6,10) and B(3,-8)?
Solution:
Assume the line segment AB is divided by point (-4, 6) in the ratio of k : 1.
After applying the Section Formula,
We will get
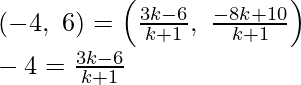
-4k -4 = 3k – 6
7k = 2
k : 1 = 2 : 7
We can also check for the y-coordinate also.
Hence,
The ratio in which the line segment AB is divided by point (-4,6) is 2 : 7.
Question 26. Find the ratio in which the y-axis divides the line segment joining the points (5, -6) and (-1, -4). Also, find the coordinates of the point of division.
Solution:
Assume P(5, -6) and Q(-1, -4) be the given points.
Consider the line segment PQ is divided by y-axis in the ratio k : 1.
After applying the Section Formula for the x-coordinate (as it’s zero)
We will get,
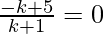
-k + 5 = 0
k = 5
Therefore,
The ratio in which the y-axis divides the given 2 points is 5 : 1
Now further, for finding the coordinates of the point of division
On putting k = 5, we will get
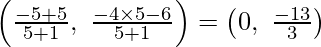
Therefore,
The coordinates of the point of division are (0, -13/3)
Question 27. Show that A(-3, 2), B(-5, 5), C(2, -3), and D(4, 4) are the vertices of a rhombus.
Solution:

Given: A(-3, 2), B(-5, 5), C(2, -3) and D(4, 4)
Further,
Mid-point of AC coordinates are 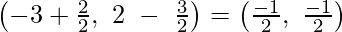
And,
Mid-point of BD coordinates are 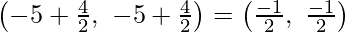
Therefore,
The mid-point for both the diagonals are the same.
Thus,
ABCD is a parallelogram.
Now,
For the sides
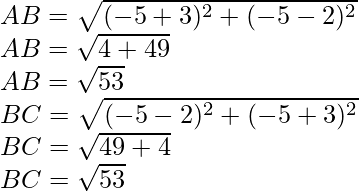
AB = BC
We can see that ABCD is a parallelogram with adjacent sides equal.
Therefore,
ABCD is a rhombus.
Question 28. Find the lengths of the medians of a ΔABC having vertices at A(0, -1), B(2, 1), and C(0, 3).
Solution:

Assume AD, BE and CF be the medians of ΔABC
Now,
Coordinates of D are 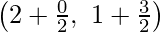 = (1, 2)
= (1, 2)
Coordinates of E are 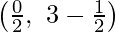 = (0, 1)
= (0, 1)
Coordinates of F are 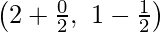 = (1, 0)
= (1, 0)
Further,
The length of the medians
Length of the median AD = 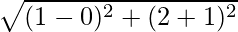 = √10 units
= √10 units
Length of the median BE = 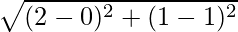 = 2 units
= 2 units
Length of the median CF = 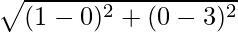 = = √10 units
= = √10 units
Question 29. Find the lengths of the median of a ΔABC having vertices at A(5, 1), B(1, 5), and C(-3, -1).
Solution:

Given: Vertices of ΔABC as A(5, 1), B(1, 5) and C(-3, -1).
Consider AD, BE and CF be the medians
Coordinates of D are 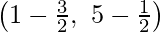 = (-1, 2)
= (-1, 2)
Coordinates of E are 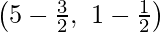 = (1, 0)
= (1, 0)
Coordinates of F are 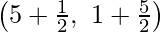 = (3, 3)
= (3, 3)
Further,
The length of the medians
Length of the median AD = 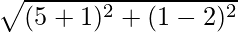 = √37 units
= √37 units
Length of the median BE = 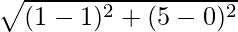 = 5 units
= 5 units
Length of the median CF =  = √52 units
= √52 units
Question 30. Find the coordinates of the point which divide the line segment joining the points (-4, 0) and (0, 6) in four equal parts.
Solution:

Consider A(-4, 0) and B(0, 6) as they are the given points
And,
Assume P, Q and R be the points which divide AB is four equal points, as shown in the fig.
Thus,
As we know that AP : PB = 1 : 3
By applying the Section Formula the coordinates of P are
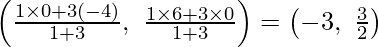
And,
We can see that Q is the mid-point of AB
Thus, the coordinates of Q are
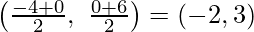
Finally,
The ratio of AR : BR is 3 : 1
Then, after applying the Section Formula the coordinates of R are
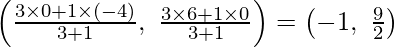
Question 31. Show that the mid-point of the line segment joining the points (5, 7) and (3, 9) is also the mid-point of the line segment joining the points (8, 6) and(0, 10).
Solution:
Assume M be the mid-point of AB. Coordinates of the mid-point of this line segment joining two points A (5, 7) and B (3, 9).
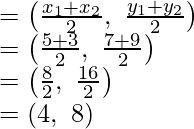
Now coordinates of the mid-point of the line segment joining the points (8, 6) and (0, 10) are;
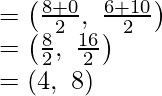
Thus, this is the same as the first case.
Question 32. Find the distance of the point (1, 2) from the mid-point of the line segment joining the points (6, 8) and (2, 4).
Solution:
Assume M be the mid-point of the line segment joining the points (6, 8) and (2, 4)
Now
Coordinates of M will be
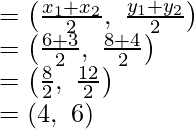
Now,
Distance between the points (4, 6) and (1, 2)
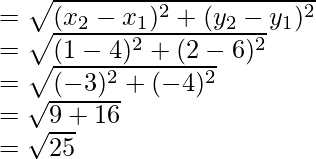 = 5 units
= 5 units
Question 33. If A and B are (1, 4) and (5, 2) respectively, find the co-ordinates of P When 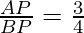
Solution:
Here, Point P divides the line segment joining the points (1, 4) and (5, 2) in the ratio of AP : PB = 3 : 4
Coordinates of P will be
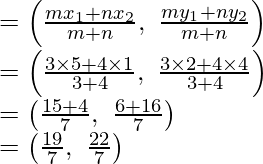
Question 34. Show that the points A (1, 0), B (5, 3), C (2, 7), and D (-2, 4) are the vertices of a parallelogram.
Solution:
If ABCD is a parallelogram,
Then its diagonal AC and BD will bisect each other at O
Consider O is the mid-point of AC,
Then coordinates of O will be;
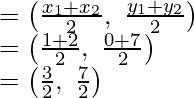
And assume O is the mid-point of BD,
Then coordinates of O will be;
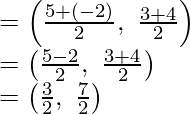
We see that coordinates of the mid-points of AC and BD are same
Therefore, AC and BD bisect each other at O
Now, length of AC
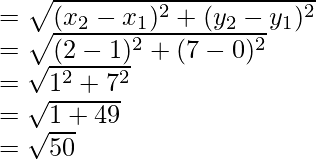
and length of BD = 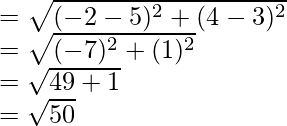
We can see that AC = BD
Therefore, ABCD is a rectangle.
Question 35. Determine the ratio in which the point P (m, 6) divides the join of A (-4, 3) and B (2, 8). Also, find the value of m.
Solution:
Assume the ratio be r : s in which P (m, 6) divides the line segment joining the points A (-4, 3) and B (2, 8)
Therefore,
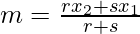
and 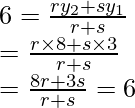
⇒ 8r + 3s = 6r + 6s
⇒ 8r – 6r = 6s – 3s
⇒ 2r = 3s
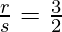
Therefore,
Ratio is 3 : 2
Now,
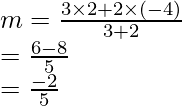
Hence, m = -2/5
Question 36. Determine the ratio in which the point (-6, a) divides the join of A (-3, -1) and B (-8, 9). Also, find the value of a.
Solution:
Assume the point P (-6, a) divides the join of A (-3, -1) and B (-8, 9) in the ratio m : n
Therefore,
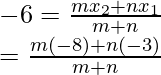
-6 = (-8m -3n)/(m + n)
-6m – 6n = -8m – 3n
8m – 6m = 6n – 3n
2m = 3n
m/n = 3/2
Therefore,
Ratio = 3 : 2
and
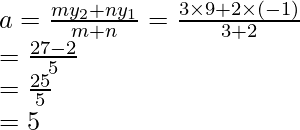
Question 37. ABCD is a rectangle formed by joining the points A (-1, -1), B (-1, 4), C (5, 4), and D (5, -1). P, Q, R, and S are the mid-points of sides AB, BC, CD, and DA respectively. Is the quadrilateral PQRS a square ? a rectangle ? or a rhombus? Justify your answer.
Solution:
ABCD is a rectangle whose vertices are A (-1,-1), B (-1,4), C (5, 4) and D (5, -1).
P, Q, R, and S are the mid-points of the sides AB, BC, CD and DA respectively
And are joined PR and QS are also joined.

Now coordinates of P will be
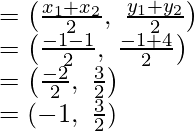
Similarly, the coordinates of Q, will be:
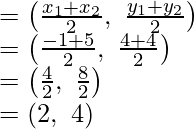
Coordinates of R will be:
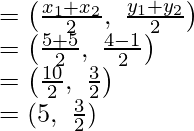
Coordinates of S will be:
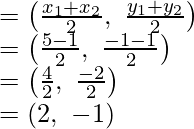
Coordinates of P (-1, 3/2), Q (2, 4), R(5, 3/2) and S (2, -1)
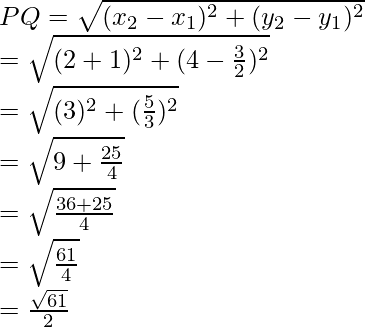
Now, assume the diagonals PQ and QS intersect each other at O
Assume O is the mid-point of PR,
Then coordinates of O will be
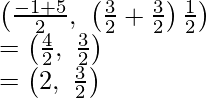
Similarly, of O is the mid-point of QS, then the coordinates of O will be
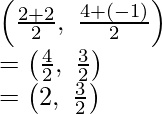
Now, we see that the coordinates of O in both case is same and adjacent sides are also equal
Then it may be a square or a rhombus
Now length of PR = 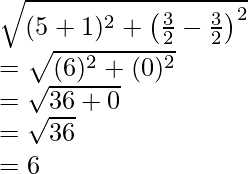
And length of OS
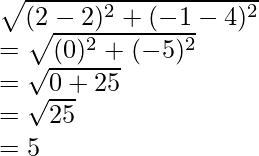
Because diagonal are not equal
Hence, PQRS is a rhombus.
Question 38. Points P, Q, R, and S divide the line segment joining the points A (1, 2) and B (6, 7) in 5 equal parts. Find the coordinates of the points P, Q, and R.
Solution:
Points P, Q, R and S divides AB in 5 equal parts and assume coordinates of P, Q, R and S are,
(x1, y1), (x2, y2), (x3, y3), (x4, y4)

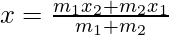
⇒ P divides AB in ratio 1 : 4
Therefore,
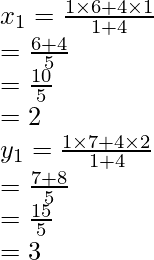
Hence, Coordinates of P are (2, 3)
⇒ Q divides AB in the ratio 2 : 3
Therefore,
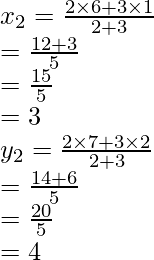
Hence, Coordinates of 3, 4
⇒ R divides AB in ration 3 : 2
Therefore,
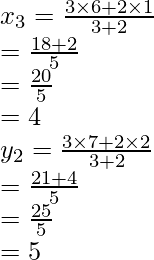
Hence, Coordinates of R are (4, 5).
Question 39. If A and B are two points having coordinates (-2, -2) and (2, -4) respectively, find the coordinates of P such that AP = 3/7 AB
Solution:
AP = 3/7 AB
7AP = 3AB
7AP = 3(AP + BP)
⇒ 7AP = 3AP + 3BP
⇒ 7AP – 3AP = 3BP
⇒ 4 AP = 3 BP
⇒ 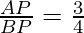
Therefore,
AP : BP = 3 : 4
Because P divides AB in the ratio of 3 : 4 whose end points are A(-2, -2) and B(2, -4)
Therefore, Coordinates of P will be
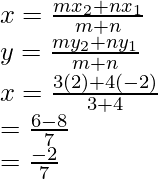
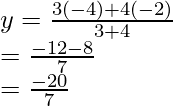
Therefore,
Coordinates of P will be 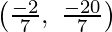
Question 40. Find the coordinates of the points which divide the line segment joining A (-2, 2) and B (2, 8) into four equal parts.
Solution:
Assume P, Q and R divides the line segment AB in four equal parts
Co-ordinates of A are (-2, 2) and of B are (2, 8)

It can be seen that Q divides AB in two equal parts while P bisects AQ and R, bisect QB.
Now,
Coordinates of Q will be :
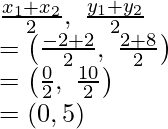
Similarly, coordinates of P will be:
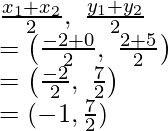
Coordinates of R will be:
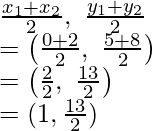
Hence, Coordinates of P are(1, 7/2)
Coordinates of Q are (0, 5)
Coordinates of R are (1, 13/2)
Share your thoughts in the comments
Please Login to comment...