2D Transformation in Computer Graphics | Set 1 (Scaling of Objects)

We can use a 2 × 2 matrix to change, or transform, a 2D vector

This kind of operation, which takes in a 2-vector and produces another 2-vector by a simple matrix multiplication, is a linear transformation.

By this simple formula we can achieve a variety of useful transformations, depending on what we put in the entries of the matrix. For our purposes, consider moving along the x-axis a horizontal move and along the y-axis, a vertical move.

 A scaling transformation alters size of an object. In the scaling process, we either compress or expand the dimension of the object. Scaling operation can be achieved by multiplying each vertex coordinate (x, y) of the polygon by scaling factor s_x and s_y to produce the transformed coordinates as (x’, y’). So, x’ = x * s_x and y’ = y * s_y. The scaling factor s_x, s_y scales the object in X and Y direction respectively. So, the above equation can be represented in matrix form: 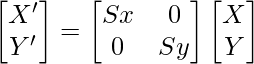Or P’ = S . P Scaling process: Note: If the scaling factor S is less than 1, then we reduce the size of the object. If the scaling factor S is greater than 1, then we increase size of the object. Algorithm:

1. Make a 2x2 scaling matrix S as:
   Sx 0
   0  Sy
2. For each point of the polygon.
   (i) Make a 2x1 matrix P, where P[0][0] equals 
       to x coordinate of the point and P[1][0] 
       equals to y coordinate of the point.
   (ii) Multiply scaling matrix S with point 
        matrix P to get the new coordinate.
3. Draw the polygon using new coordinates.

Below is C implementation: 

C

// C program to demonstrate scaling of abjects
#include<stdio.h>
#include<graphics.h>

// Matrix Multiplication to find new Coordinates.
// s[][] is scaling matrix. p[][] is to store
// points that needs to be scaled.
// p[0][0] is x coordinate of point.
// p[1][0] is y coordinate of given point.
void findNewCoordinate(int s[][2], int p[][1])
{
    int temp[2][1] = { 0 };

    for (int i = 0; i < 2; i++)
        for (int j = 0; j < 1; j++)
            for (int k = 0; k < 2; k++)
                temp[i][j] += (s[i][k] * p[k][j]);

    p[0][0] = temp[0][0];
    p[1][0] = temp[1][0];
}

// Scaling the Polygon
void scale(int x[], int y[], int sx, int sy)
{
    // Triangle before Scaling
    line(x[0], y[0], x[1], y[1]);
    line(x[1], y[1], x[2], y[2]);
    line(x[2], y[2], x[0], y[0]);

    // Initializing the Scaling Matrix.
    int s[2][2] = { sx, 0, 0, sy };
    int p[2][1];

    // Scaling the triangle
    for (int i = 0; i < 3; i++)
    {
        p[0][0] = x[i];
        p[1][0] = y[i];

        findNewCoordinate(s, p);

        x[i] = p[0][0];
        y[i] = p[1][0];
    }

    // Triangle after Scaling
    line(x[0], y[0], x[1], y[1]);
    line(x[1], y[1], x[2], y[2]);
    line(x[2], y[2], x[0], y[0]);
}

// Driven Program
int main()
{
    int x[] = { 100, 200, 300 };
    int y[] = { 200, 100, 200 };
    int sx = 2, sy = 2;

    int gd, gm;
    detectgraph(&gd, &gm);
    initgraph(&gd, &gm," ");

    scale(x, y, sx,sy);
    getch();

    return 0;
}

Output:    This article is contributed by Anuj Chauhan. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks. Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.