Window to Viewport Transformation in Computer Graphics with Implementation

Window to Viewport Transformation is the process of transforming 2D world-coordinate objects to device coordinates. Objects inside the world or clipping window are mapped to the viewport which is the area on the screen where world coordinates are mapped to be displayed.

General Terms: 

• World coordinate – It is the Cartesian coordinate w.r.t which we define the diagram, like X_wmin, X_wmax, Y_wmin, Y_wmax
• Device Coordinate –It is the screen coordinate where the objects are to be displayed, like X_vmin, X_vmax, Y_vmin, Y_vmax
• Window –It is the area on the world coordinate selected for display.
• ViewPort –It is the area on the device coordinate where graphics is to be displayed.

Mathematical Calculation of Window to Viewport: 

It may be possible that the size of the Viewport is much smaller or greater than the Window. In these cases, we have to increase or decrease the size of the Window according to the Viewport and for this, we need some mathematical calculations.

(xw, yw): A point on Window
(xv, yv): Corresponding  point on Viewport

We have to calculate the point (x_v, y_v)

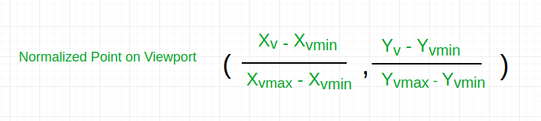
Now the relative position of the object in Window and Viewport are same.

For x coordinate,                        

 For y coordinate,

So, after calculating for x and y coordinate, we get

Where s_x is the scaling factor of x coordinate and s_y is the scaling factor of y coordinate

Example: Let us assume, 

• for window, X_wmin = 20, X_wmax = 80, Y_wmin = 40, Y_wmax = 80.
• for viewport, X_vmin = 30, X_vmax = 60, Y_vmin = 40, Y_vmax = 60.
• Now a point ( X_w, Y_w ) be ( 30, 80 ) on the window. We have to calculate that point on the viewport 
  i.e ( X_v, Y_v ).
• First of all, calculate the scaling factor of x coordinate S_x and the scaling factor of y coordinate S_y using the above-mentioned formula.

Sx = ( 60 - 30 ) / ( 80 - 20 ) = 30 / 60
Sy = ( 60 - 40 ) / ( 80 - 40 ) = 20 / 40

• So, now calculate the point on the viewport ( X_v, Y_v ).

Xv = 30 + ( 30 - 20 ) * ( 30 / 60 ) = 35
Yv = 40 + ( 80 - 40 ) * ( 20 / 40 ) = 60

• So, the point on window ( X_w, Y_w ) = ( 30, 80 ) will be ( X_v, Y_v ) = ( 35, 60 ) on viewport.

Here is the implementation of the above approach:

C++

// C++ program to implement
// Window to ViewPort Transformation

#include <iostream>
using namespace std;

// Function for window to viewport transformation
void WindowtoViewport(int x_w, int y_w, int x_wmax,
                      int y_wmax, int x_wmin, int y_wmin,
                      int x_vmax, int y_vmax, int x_vmin,
                      int y_vmin)
{
    // point on viewport
    int x_v, y_v;

    // scaling factors for x coordinate and y coordinate
    float sx, sy;

    // calculating Sx and Sy
    sx = (float)(x_vmax - x_vmin) / (x_wmax - x_wmin);
    sy = (float)(y_vmax - y_vmin) / (y_wmax - y_wmin);

    // calculating the point on viewport
    x_v = x_vmin + (float)((x_w - x_wmin) * sx);
    y_v = y_vmin + (float)((y_w - y_wmin) * sy);

    cout<< "The point on viewport: ("<<x_v  <<","<< y_v<<")" ;
}

// Driver Code
int main()
{
    // boundary values for window
    int x_wmax = 80, y_wmax = 80, x_wmin = 20, y_wmin = 40;

    // boundary values for viewport
    int x_vmax = 60, y_vmax = 60, x_vmin = 30, y_vmin = 40;

    // point on window
    int x_w = 30, y_w = 80;

    WindowtoViewport(30, 80, 80, 80, 20, 40, 60, 60, 30, 40);
}

// This code is contributed by khusboogoyal499.

C

// C program to implement
// Window to ViewPort Transformation

#include <stdio.h>

// Function for window to viewport transformation
void WindowtoViewport(int x_w, int y_w, int x_wmax,
                      int y_wmax, int x_wmin, int y_wmin,
                      int x_vmax, int y_vmax, int x_vmin,
                      int y_vmin)
{
    // point on viewport
    int x_v, y_v;

    // scaling factors for x coordinate and y coordinate
    float sx, sy;

    // calculating Sx and Sy
    sx = (float)(x_vmax - x_vmin) / (x_wmax - x_wmin);
    sy = (float)(y_vmax - y_vmin) / (y_wmax - y_wmin);

    // calculating the point on viewport
    x_v = x_vmin + (float)((x_w - x_wmin) * sx);
    y_v = y_vmin + (float)((y_w - y_wmin) * sy);

    printf("The point on viewport: (%d, %d )\n ", x_v, y_v);
}

// Driver Code
void main()
{
    // boundary values for window
    int x_wmax = 80, y_wmax = 80, x_wmin = 20, y_wmin = 40;

    // boundary values for viewport
    int x_vmax = 60, y_vmax = 60, x_vmin = 30, y_vmin = 40;

    // point on window
    int x_w = 30, y_w = 80;

    WindowtoViewport(30, 80, 80, 80, 20, 40, 60, 60, 30, 40);
}

//this code is added by khushboogoyal499

Java

// Java program to implement
// Window to ViewPort Transformation
class GFG
{

// Function for window to viewport transformation
static void WindowtoViewport(int x_w, int y_w, int x_wmax,
                    int y_wmax, int x_wmin, int y_wmin,
                    int x_vmax, int y_vmax, int x_vmin,
                    int y_vmin)
{
    // point on viewport
    int x_v, y_v;

    // scaling factors for x coordinate and y coordinate
    float sx, sy;

    // calculating Sx and Sy
    sx = (float)(x_vmax - x_vmin) / (x_wmax - x_wmin);
    sy = (float)(y_vmax - y_vmin) / (y_wmax - y_wmin);

    // calculating the point on viewport
    x_v = (int) (x_vmin + (float)((x_w - x_wmin) * sx));
    y_v = (int) (y_vmin + (float)((y_w - y_wmin) * sy));

    System.out.printf("The point on viewport: (%d, %d )\n ", x_v, y_v);
}

// Driver Code
public static void main(String[] args)
{

    // boundary values for window
    int x_wmax = 80, y_wmax = 80, x_wmin = 20, y_wmin = 40;

    // boundary values for viewport
    int x_vmax = 60, y_vmax = 60, x_vmin = 30, y_vmin = 40;

    // point on window
    int x_w = 30, y_w = 80;

    WindowtoViewport(30, 80, 80, 80, 20, 40, 60, 60, 30, 40);
}
}

// This code is contributed by Rajput-Ji

Python3

# Python3 program to implement
# Window to ViewPort Transformation

# Function for window to viewport transformation
def WindowtoViewport(x_w, y_w, x_wmax, y_wmax,
                       x_wmin, y_wmin, x_vmax,
                       y_vmax, x_vmin, y_vmin):

    # point on viewport
    # calculating Sx and Sy
    sx = (x_vmax - x_vmin) / (x_wmax - x_wmin)
    sy = (y_vmax - y_vmin) / (y_wmax - y_wmin)

    # calculating the point on viewport
    x_v = x_vmin + ((x_w - x_wmin) * sx)
    y_v = y_vmin + ((y_w - y_wmin) * sy)

    print("The point on viewport:(", int(x_v),
                                ",", int(y_v), ")")

# Driver Code
if __name__ == '__main__':

    # boundary values for window
    x_wmax = 80
    y_wmax = 80
    x_wmin = 20
    y_wmin = 40

    # boundary values for viewport
    x_vmax = 60
    y_vmax = 60
    x_vmin = 30
    y_vmin = 40

    # point on window
    x_w = 30
    y_w = 80

    WindowtoViewport(30, 80, 80, 80, 20,
                     40, 60, 60, 30, 40)

# This code is contributed by Surendra_Gangwar

C#

// C# program to implement
// Window to ViewPort Transformation
using System;

class GFG
{

// Function for window to viewport transformation
static void WindowtoViewport(int x_w, int y_w,
                             int x_wmax, int y_wmax,
                             int x_wmin, int y_wmin,
                             int x_vmax, int y_vmax,
                             int x_vmin, int y_vmin)
{
    // point on viewport
    int x_v, y_v;

    // scaling factors for x coordinate
    // and y coordinate
    float sx, sy;

    // calculating Sx and Sy
    sx = (float)(x_vmax - x_vmin) /
                (x_wmax - x_wmin);
    sy = (float)(y_vmax - y_vmin) /
                (y_wmax - y_wmin);

    // calculating the point on viewport
    x_v = (int) (x_vmin +
        (float)((x_w - x_wmin) * sx));
    y_v = (int) (y_vmin +
        (float)((y_w - y_wmin) * sy));

    Console.Write("The point on viewport: " +
                 "({0}, {1} )\n ", x_v, y_v);
}

// Driver Code
public static void Main(String[] args)
{

    // boundary values for window
    int x_wmax = 80, y_wmax = 80,
        x_wmin = 20, y_wmin = 40;

    // boundary values for viewport
    int x_vmax = 60, y_vmax = 60,
        x_vmin = 30, y_vmin = 40;

    // point on window
    int x_w = 30, y_w = 80;

    WindowtoViewport(30, 80, 80, 80, 20,
                     40, 60, 60, 30, 40);
}
}

// This code is contributed by PrinciRaj1992

Javascript

<script>
// Javascript program to implement
// Window to ViewPort Transformation

// Function for window to viewport transformation
function WindowtoViewport(x_w, y_w, x_wmax,y_wmax, x_wmin,
                    y_wmin,x_vmax, y_vmax, x_vmin,y_vmin)
{
    // point on viewport
    let x_v, y_v;

    // scaling factors for x coordinate and y coordinate
    let sx, sy;

    // calculating Sx and Sy
    sx = (x_vmax - x_vmin) / (x_wmax - x_wmin);
    sy = (y_vmax - y_vmin) / (y_wmax - y_wmin);

    // calculating the point on viewport
    x_v = x_vmin + ((x_w - x_wmin) * sx);
    y_v = y_vmin + ((y_w - y_wmin) * sy);

    document.write("The point on viewport: (" + x_v + ", "
                                + y_v + " )<br>");
}

// Driver Code
    // boundary values for window
    let x_wmax = 80, y_wmax = 80, x_wmin = 20, y_wmin = 40;

    // boundary values for viewport
    let x_vmax = 60, y_vmax = 60, x_vmin = 30, y_vmin = 40;

    // point on window
    let x_w = 30, y_w = 80;

    WindowtoViewport(30, 80, 80, 80, 20, 40, 60, 60, 30, 40);

</script>

Output:

The point on viewport: (35, 60 )

Time Complexity: O(1), as we are not using any looping statements.

Space Complexity: O(1) , as we are not using any extra space.