3-D Transformation is the process of manipulating the view of a three-D object with respect to its original position by modifying its physical attributes through various methods of transformation like Translation, Scaling, Rotation, Shear, etc.
Types of Transformation:
- Translation Transformation
- Scaling Transformation
- Rotation Transformation
- Shearing Transformation
- Reflection Transformation
Note: If we’re asked to perform three or more different sorts of transformations over a point(P0) simultaneously which is placed in 3D space, and let us assume that these transformations are T1, T2, and T3 respectively, then in this case what we’ll do?
So, we will see the following solutions
a) Obviously, first by applying series of Transformations one by one over the coordinates of the object sequentially.
First we performed transformation T1, then Po become transformed to P1.
Secondly, we perform transformation T2 and the point P1 become transformed to P2.
Lastly, we perform transformation T3 and we get the final result i.e; P3,and we will get our final transformed point coordinate(P3).
b) Second solution, by applying Composite transformation in a single shot.
![Rendered by QuickLaTeX.com \mathbf{P_1[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=P_0[x_0\hspace{0.2cm}y_0\hspace{0.2cm}z_0\hspace{0.2cm}1].T_1} \newline \hspace{5.87cm}\mathbf{P_1[x\hspace{0.2cm}y\hspace{0.2cm}z]=[x_1\hspace{0.2cm}y_1\hspace{0.2cm}z_1]} \\ \hspace{4.37cm}\mathbf{P_2[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=P_1[x_1\hspace{0.2cm}y_1\hspace{0.2cm}z_1\hspace{0.2cm}1].T_2} \newline \hspace{5.87cm}\mathbf{P_2[x\hspace{0.2cm}y\hspace{0.2cm}z]=[x_2\hspace{0.2cm}y_2\hspace{0.2cm}z_2]} \newline \hspace{4.37cm}\mathbf{P_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=P_2[x_2\hspace{0.2cm}y_2\hspace{0.2cm}z_2\hspace{0.2cm}1].T_3} \newline \hspace{5.87cm}\mathbf{P_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[x_3\hspace{0.2cm}y_3\hspace{0.2cm}z_3]}\\ \textbf {But the idea that is concerned in Composite Transformation is} \newline \textbf{slightly different, that we'll discuss in detail in the following article.}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e2b879dda5a3b1fc3e31cad2c8a1ddc3_l3.png)
Note: Here T1, T2, T3 correspond to their transformation matrix condition.
Composite Transformation
As its name suggests itself composite, here we compose two or more than two transformations together and calculate a resultant(R) transformation matrix by multiplying all the corresponding transformation matrix conditions with each other.
The same equivalent result that we got over Point P0 and transformed it into P3 in the above example can also be achieved by directly multiplying resultant R with the point P0 rather than performing transformations T1, T2, and T3 sequentially one after one.
![Rendered by QuickLaTeX.com \mathbf{R=[T_1*T_2*T_3]} \newline \hspace{4.37cm}\mathbf{P_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=P_0[x_0\hspace{0.2cm}y_0\hspace{0.2cm}z_0\hspace{0.2cm}1].R} \\ \hspace{5.87cm}\mathbf{P_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[x_3\hspace{0.2cm}y_3\hspace{0.2cm}z_3]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-467fc950ba14904f1611ef6546104f8f_l3.png)
And we end up with the same equivalent result that we got into our above example.
Problem: Consider we are given with a cuboid “OABCDEFG” over which we want to perform
- Translation transformation(T1) if translation distances are Dx=2, Dy=3, Dz=2 ,then
- Scaling transformation(T2) if scaling factors are sx=2, sy=1, sz=3 and lastly perform,
- Shearing transformation(T3) in x-direction if shearing factors are sy=2 and sz=1.
Solution: We are given the following cuboid
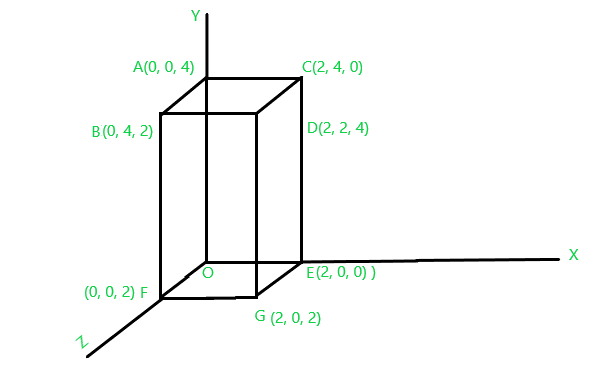
Fig.1
First, we perform translation transformation T1:
The Translation transformation matrix is shown as:
![Rendered by QuickLaTeX.com \mathbf{T_1=\left[\begin{matrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\D_x&D_y&D_z&1\end{matrix}\right]}\\ \mathbf{Where \hspace{0.2cm}D_x=2,D_y=3\hspace{0.2cm} and\hspace{0.2cm} D_z=3\hspace{0.2cm} are\hspace{0.2cm}translation\hspace{0.2cm} distances.}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f36cdff35de11139b78596d588a090be_l3.png) [Tex]\hspace{4.37cm}\mathbf{T_1=\left[\begin{matrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\D_x&D_y&D_z&1\end{matrix}\right]}\\ \mathbf{Where \hspace{0.2cm}D_x=2,D_y=3\hspace{0.2cm} and\hspace{0.2cm} D_z=3\hspace{0.2cm} are\hspace{0.2cm}translation\hspace{0.2cm} distances.} [/Tex]
[Tex]\hspace{4.37cm}\mathbf{T_1=\left[\begin{matrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\D_x&D_y&D_z&1\end{matrix}\right]}\\ \mathbf{Where \hspace{0.2cm}D_x=2,D_y=3\hspace{0.2cm} and\hspace{0.2cm} D_z=3\hspace{0.2cm} are\hspace{0.2cm}translation\hspace{0.2cm} distances.} [/Tex]
Now apply this translation transformation matrix condition over the coordinates:
For coordinate O[0 0 0], the newly translated coordinate would be O1:
![Rendered by QuickLaTeX.com \mathbf{O_1[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=O[0\hspace{0.2cm}0\hspace{0.2cm}0\hspace{0.2cm}1]*\left[\begin{matrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\2&3&2&1\end{matrix}\right]}\\ \\ \hspace{6.52cm}\mathbf{=[2\hspace{0.2cm}3\hspace{0.2cm}2\hspace{0.2cm}1]} \\ \hspace{4.15cm}\mathbf{O_1[x\hspace{0.2cm}y\hspace{0.2cm}z]=[2\hspace{0.2cm}3\hspace{0.2cm}2]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-922d14dc895eb80c7276b3f11b449727_l3.png)
For coordinate A[0 0 4], the newly translated coordinate would be A1:
![Rendered by QuickLaTeX.com \mathbf{A_1[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=A[0\hspace{0.2cm}0\hspace{0.2cm}0\hspace{0.2cm}1]*\left[\begin{matrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\2&3&2&1\end{matrix}\right]}\\ \\ \hspace{6.52cm}\mathbf{=[2\hspace{0.2cm}3\hspace{0.2cm}6\hspace{0.2cm}1]} \\ \hspace{4.15cm}\mathbf{A_1[x\hspace{0.2cm}y\hspace{0.2cm}z]=[2\hspace{0.2cm}3\hspace{0.2cm}6]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2d38994ba76df0036934610476e68c92_l3.png)
For coordinate B[0 4 2], the newly translated coordinate would be B1:
![Rendered by QuickLaTeX.com \mathbf{B_1[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=B[0\hspace{0.2cm}4\hspace{0.2cm}2\hspace{0.2cm}1]*\left[\begin{matrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\2&3&2&1\end{matrix}\right]}\\ \\ \hspace{6.52cm}\mathbf{=[2\hspace{0.2cm}7\hspace{0.2cm}4\hspace{0.2cm}1]} \\ \hspace{4.15cm}\mathbf{B_1[x\hspace{0.2cm}y\hspace{0.2cm}z]=[2\hspace{0.2cm}7\hspace{0.2cm}4]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d3665cee50645079c5e9d11a25ed4dbb_l3.png)
For coordinate C[2 4 0], the newly translated coordinate would be C1:
![Rendered by QuickLaTeX.com \mathbf{C_1[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=C[2\hspace{0.2cm}4\hspace{0.2cm}0\hspace{0.2cm}1]*\left[\begin{matrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\2&3&2&1\end{matrix}\right]}\\ \\ \hspace{6.52cm}\mathbf{=[4\hspace{0.2cm}7\hspace{0.2cm}2\hspace{0.2cm}1]} \\ \hspace{4.15cm}\mathbf{C_1[x\hspace{0.2cm}y\hspace{0.2cm}z]=[4\hspace{0.2cm}7\hspace{0.2cm}2]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4f97c7aad24df8372eae818c7efd67fa_l3.png)
For coordinate D[2 2 4], the newly translated coordinate would be D1:
![Rendered by QuickLaTeX.com \mathbf{D_1[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=D[2\hspace{0.2cm}2\hspace{0.2cm}4\hspace{0.2cm}1]*\left[\begin{matrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\2&3&2&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[4\hspace{0.2cm}5\hspace{0.2cm}6\hspace{0.2cm}1]} \\ \hspace{4.15cm}\mathbf{D_1[x\hspace{0.2cm}y\hspace{0.2cm}z]=[4\hspace{0.2cm}5\hspace{0.2cm}6]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ac05ca0b3f7c4ba13c776ca6e556a4e8_l3.png)
For coordinate E[2 0 0], the newly translated coordinate would be E1:
![Rendered by QuickLaTeX.com \mathbf{E_1[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=E[2\hspace{0.2cm}0\hspace{0.2cm}0\hspace{0.2cm}1]*\left[\begin{matrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\2&3&2&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[4\hspace{0.2cm}3\hspace{0.2cm}2\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{E_1[x\hspace{0.2cm}y\hspace{0.2cm}z]=[4\hspace{0.2cm}3\hspace{0.2cm}2]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8302a6077300b7873c3e009f700c39c4_l3.png)
For coordinate F[0 0 2], the newly translated coordinate would be F1:
![Rendered by QuickLaTeX.com \mathbf{F_1[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=F[0\hspace{0.2cm}0\hspace{0.2cm}2\hspace{0.2cm}1]*\left[\begin{matrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\2&3&2&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[2\hspace{0.2cm}3\hspace{0.2cm}4\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{F_1[x\hspace{0.2cm}y\hspace{0.2cm}z]=[2\hspace{0.2cm}3\hspace{0.2cm}4]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-46b88e7ac963f080d523ed8f2fbe1401_l3.png)
For coordinate G[2 0 2], the newly translated coordinate would be G1:
![Rendered by QuickLaTeX.com \mathbf{G_1[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=G[2\hspace{0.2cm}0\hspace{0.2cm}2\hspace{0.2cm}1]*\left[\begin{matrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\2&3&2&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[4\hspace{0.2cm}3\hspace{0.2cm}4\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{G_1[x\hspace{0.2cm}y\hspace{0.2cm}z]=[4\hspace{0.2cm}3\hspace{0.2cm}4]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-476afc6badfe3225bb9079f5f0a796e2_l3.png)

Fig.2
Secondly, we are said to perform Scaling transformation T2:
The Scaling transformation matrix is shown as:
![Rendered by QuickLaTeX.com \hspace{4.37cm}\mathbf{T_2=\left[\begin{matrix}s_x&0&0&0\\0&s_y&0&0\\0&0&s_z&0\\D_x&D_y&D_z&1\end{matrix}\right]}\\ \mathbf{Where \hspace{0.2cm}s_x=2,s_y=1\hspace{0.2cm} and\hspace{0.2cm} s_z=3\hspace{0.2cm} are\hspace{0.2cm}Scaling\hspace{0.2cm}parameter.}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6dc4aacdd490889ad648695e336127e8_l3.png)
Now apply this Scaling transformation matrix condition over the coordinates:
For coordinate O1[2 3 2], the newly Scaled coordinate would be O2:
![Rendered by QuickLaTeX.com \mathbf{O_2[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=O_1[2\hspace{0.2cm}3\hspace{0.2cm}2\hspace{0.2cm}1]*\left[\begin{matrix}2&0&0&0\\0&1&0&0\\0&0&3&0\\0&0&0&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[4\hspace{0.2cm}3\hspace{0.2cm}6\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{O_2[x\hspace{0.2cm}y\hspace{0.2cm}z]=[4\hspace{0.2cm}3\hspace{0.2cm}6]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-85a0c0f9309dc2964f0d72e6f4aaaa41_l3.png)
For coordinate A1[2 3 6], the newly Scaled coordinate would be A2:
![Rendered by QuickLaTeX.com \mathbf{A_2[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=A_1[2\hspace{0.2cm}3\hspace{0.2cm}6\hspace{0.2cm}1]*\left[\begin{matrix}2&0&0&0\\0&1&0&0\\0&0&3&0\\0&0&0&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[4\hspace{0.2cm}3\hspace{0.2cm}18\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{A_2[x\hspace{0.2cm}y\hspace{0.2cm}z]=[4\hspace{0.2cm}3\hspace{0.2cm}18]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0c3229f9e6feab34f5ed00903960d57f_l3.png)
For coordinate B1[2 7 4], the newly Scaled coordinate would be B2:
![Rendered by QuickLaTeX.com \mathbf{B_2[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=B_1[2\hspace{0.2cm}7\hspace{0.2cm}4\hspace{0.2cm}1]*\left[\begin{matrix}2&0&0&0\\0&1&0&0\\0&0&3&0\\0&0&0&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[4\hspace{0.2cm}7\hspace{0.2cm}12\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{B_2[x\hspace{0.2cm}y\hspace{0.2cm}z]=[4\hspace{0.2cm}7\hspace{0.2cm}12]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bb874ffc5afcec6f79a29850502f2cfd_l3.png)
For coordinate C1[4 7 2], the newly Scaled coordinate would be C2:
![Rendered by QuickLaTeX.com \mathbf{C_2[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=C_1[2\hspace{0.2cm}3\hspace{0.2cm}6\hspace{0.2cm}1]*\left[\begin{matrix}2&0&0&0\\0&1&0&0\\0&0&3&0\\0&0&0&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[8\hspace{0.2cm}7\hspace{0.2cm}6\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{C_2[x\hspace{0.2cm}y\hspace{0.2cm}z]=[8\hspace{0.2cm}7\hspace{0.2cm}6]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-635affa20cf5eec1bd27162583bf04ef_l3.png)
For coordinate D1[4 5 6], the newly Scaled coordinate would be D2:
![Rendered by QuickLaTeX.com \mathbf{D_2[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=D_1[4\hspace{0.2cm}5\hspace{0.2cm}6\hspace{0.2cm}1]*\left[\begin{matrix}2&0&0&0\\0&1&0&0\\0&0&3&0\\0&0&0&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[8\hspace{0.2cm}5\hspace{0.2cm}18\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{D_2[x\hspace{0.2cm}y\hspace{0.2cm}z]=[8\hspace{0.2cm}5\hspace{0.2cm}18]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-08a5f637b881022732b493fc699a39a2_l3.png)
For coordinate E1[4 3 2], the newly Scaled coordinate would be E2:
![Rendered by QuickLaTeX.com \mathbf{E_2[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=E_1[4\hspace{0.2cm}3\hspace{0.2cm}2\hspace{0.2cm}1]*\left[\begin{matrix}2&0&0&0\\0&1&0&0\\0&0&3&0\\0&0&0&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[8\hspace{0.2cm}3\hspace{0.2cm}6\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{E_2[x\hspace{0.2cm}y\hspace{0.2cm}z]=[8\hspace{0.2cm}3\hspace{0.2cm}6]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9b8a3f40cc62dfe111538530cdd2fc2a_l3.png)
For coordinate F1[2 3 4], the newly Scaled coordinate would be F2:
![Rendered by QuickLaTeX.com \mathbf{F_2[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=F_1[2\hspace{0.2cm}3\hspace{0.2cm}4\hspace{0.2cm}1]*\left[\begin{matrix}2&0&0&0\\0&1&0&0\\0&0&3&0\\0&0&0&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[4\hspace{0.2cm}3\hspace{0.2cm}12\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{F_2[x\hspace{0.2cm}y\hspace{0.2cm}z]=[4\hspace{0.2cm}3\hspace{0.2cm}12]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d94164639c65153d5a3625668d69cc74_l3.png)
For coordinate G1[4 3 4], the newly Scaled coordinate would be G2:
![Rendered by QuickLaTeX.com \mathbf{G_2[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=G_1[4\hspace{0.2cm}3\hspace{0.2cm}4\hspace{0.2cm}1]*\left[\begin{matrix}2&0&0&0\\0&1&0&0\\0&0&3&0\\0&0&0&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[8\hspace{0.2cm}3\hspace{0.2cm}12\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{G_2[x\hspace{0.2cm}y\hspace{0.2cm}z]=[8\hspace{0.2cm}3\hspace{0.2cm}12]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-73d1c28bbb7590c989491f11a1e2b5b5_l3.png)

Fig.3
Lastly, we perform Shearing transformation T3 in x-direction:
The Shearing transformation matrix for x-direction is shown as:
![Rendered by QuickLaTeX.com \hspace{4.37cm}\mathbf{T_3=\left[\begin{matrix}1&sh_y&sh_z&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{matrix}\right]}\\ \mathbf{Where \hspace{0.2cm}sh_y=2\hspace{0.2cm}and\hspace{0.2cm}sh_z=1\hspace{0.2cm}are\hspace{0.2cm}Shearing\hspace{0.2cm}parameter.}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f75e4183fead684ccb775327b3726cbb_l3.png)
Now, apply this Shearing transformation matrix condition over the coordinates:
For coordinate O2[4 3 6], the newly Scaled coordinate would be O3:
![Rendered by QuickLaTeX.com \mathbf{O_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=O_2[4\hspace{0.2cm}3\hspace{0.2cm}6\hspace{0.2cm}1]*\left[\begin{matrix}1&2&1&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[4\hspace{0.2cm}11\hspace{0.2cm}10\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{O_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[4\hspace{0.2cm}11\hspace{0.2cm}10]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8ef986647129a88f4e65053ff7071285_l3.png)
For coordinate A2[4 3 18], the newly Scaled coordinate would be A3:
![Rendered by QuickLaTeX.com \mathbf{A_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=A_2[4\hspace{0.2cm}3\hspace{0.2cm}18\hspace{0.2cm}1]*\left[\begin{matrix}1&2&1&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[4\hspace{0.2cm}11\hspace{0.2cm}22\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{A_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[4\hspace{0.2cm}11\hspace{0.2cm}22]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-16b567b04c2ca915d130de89e9e2d9cf_l3.png)
For coordinate B2[4 7 12], the newly Scaled coordinate would be B3:
![Rendered by QuickLaTeX.com \mathbf{B_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=B_2[4\hspace{0.2cm}7\hspace{0.2cm}12\hspace{0.2cm}1]*\left[\begin{matrix}1&2&1&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[4\hspace{0.2cm}15\hspace{0.2cm}16\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{B_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[4\hspace{0.2cm}15\hspace{0.2cm}16]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8f803827e089d9fb55be5318decf964f_l3.png)
For coordinate C2[8 7 6], the newly Scaled coordinate would be C3:
![Rendered by QuickLaTeX.com \mathbf{C_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=C_2[8\hspace{0.2cm}7\hspace{0.2cm}6\hspace{0.2cm}1]*\left[\begin{matrix}1&2&1&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[8\hspace{0.2cm}23\hspace{0.2cm}14\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{C_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[8\hspace{0.2cm}23\hspace{0.2cm}14]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0b1ce752ecc98d24f210fdfa6e4ee65b_l3.png)
For coordinate D2[8 5 18], the newly Scaled coordinate would be D3:
![Rendered by QuickLaTeX.com \mathbf{D_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=D_2[8\hspace{0.2cm}6\hspace{0.2cm}18\hspace{0.2cm}1]*\left[\begin{matrix}1&2&1&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[8\hspace{0.2cm}21\hspace{0.2cm}26\hspace{0.2cm}1]} \\ \hspace{4.15cm}\mathbf{D_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[8\hspace{0.2cm}21\hspace{0.2cm}26]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3004d4ea91076d13ca8709641f557dee_l3.png)
For coordinate E2[8 7 6], the newly Scaled coordinate would be E3:
![Rendered by QuickLaTeX.com \mathbf{E_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=E_2[8\hspace{0.2cm}3\hspace{0.2cm}6\hspace{0.2cm}1]*\left[\begin{matrix}1&2&1&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{matrix}\right]}\\ \\ \hspace{6.52cm}\mathbf{=[8\hspace{0.2cm}19\hspace{0.2cm}14\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{E_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[8\hspace{0.2cm}19\hspace{0.2cm}14]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6c804ea8a97cadb392b4941e755347eb_l3.png)
For coordinate F2[4 3 12], the newly Scaled coordinate would be F3:
![Rendered by QuickLaTeX.com \mathbf{F_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=F_2[4\hspace{0.2cm}3\hspace{0.2cm}12\hspace{0.2cm}1]*\left[\begin{matrix}1&2&1&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[4\hspace{0.2cm}11\hspace{0.2cm}16\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{F_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[4\hspace{0.2cm}11\hspace{0.2cm}16]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8cab7ab12d1374db182ee681743486e5_l3.png)
For coordinate G2[8 3 12], the newly Scaled coordinate would be G3:
![Rendered by QuickLaTeX.com \mathbf{G_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=G_2[8\hspace{0.2cm}3\hspace{0.2cm}12\hspace{0.2cm}1]*\left[\begin{matrix}1&2&1&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[8\hspace{0.2cm}19\hspace{0.2cm}20\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{G_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[8\hspace{0.2cm}19\hspace{0.2cm}20]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e05e987410f86171a2ae0b74642f1471_l3.png)
Finally, we get our resized slanted object in the x-direction after performing transformations T1, T2 and T3.

Fig.4
Solution through Composite Transformation
The final result, that we got above for the cuboid “OABCDEF” through applying transformation T1, T2, and T3 one after one in sequential order the same equivalent result could also be got by using the concept of Composite Transformation. To perform composite transformation first we need to calculate the Resultant Transformation matrix(R) by combining all the distinguished transformation matrix representations together.
The resultant transformation matrix would be calculated as follows:
The resultant transformation will be calculated by multiplying the Translation transformation matrix with the Scaling transformation matrix and the resultant(R2) multiplication of both will then be multiplied with the last given, Shearing transformation matrix.
![Rendered by QuickLaTeX.com \hspace{4.37cm}\mathbf{R_2=\left[\begin{matrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\2&3&2&1\end{matrix}\right]*\mathbf{\left[\begin{matrix}2&0&0&0\\0&1&0&0\\0&0&3&0\\0&0&0&1\end{matrix}\right]}} \\ \newline\hspace{4.37cm}\mathbf{R_2=\left[\begin{matrix}2&0&0&0\\0&1&0&0\\0&0&3&0\\4&3&6&1\end{matrix}\right]}\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5e5a3f27c0c28a686650cfa2d84080d2_l3.png)
Now, multiply R2 with the Shearing transformation matrix to get resultant R:
![Rendered by QuickLaTeX.com \mathbf{R=R_2*\left[\begin{matrix}1&2&1&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{matrix}\right]}\\\hspace{2.87cm}\mathbf{R=\left[\begin{matrix}2&0&0&0\\0&1&0&0\\0&0&3&0\\4&3&6&1\end{matrix}\right]*\left[\begin{matrix}1&2&1&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{matrix}\right]}\\ \newline \hspace{4.15cm} \mathbf{R=\left[\begin{matrix}2&4&2&0\\0&1&0&0\\0&0&3&0\\4&11&10&1\end{matrix}\right]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-94e723cf5a255f836ce4c6e7fb87ad03_l3.png) \
\
Now, apply this resultant transformation matrix condition over the coordinates:
For coordinate O[0 0 0], the new Scaled coordinate would be O3:
![Rendered by QuickLaTeX.com \mathbf{O_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=O[0\hspace{0.2cm}0\hspace{0.2cm}0\hspace{0.2cm}1]*\left[\begin{matrix}2&4&2&0\\0&1&0&0\\0&0&3&0\\4&11&10&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[4\hspace{0.2cm}11\hspace{0.2cm}10\hspace{0.2cm}1]} \\ \hspace{4.15cm}\mathbf{O_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[4\hspace{0.2cm}11\hspace{0.2cm}10]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e3f49451a249589ee6c6a9d8542b7ca2_l3.png)
For coordinate A[0 0 4], the newly Scaled coordinate would be A3:
![Rendered by QuickLaTeX.com \mathbf{A_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=A[0\hspace{0.2cm}0\hspace{0.2cm}4\hspace{0.2cm}1]*\left[\begin{matrix}2&4&2&0\\0&1&0&0\\0&0&3&0\\4&11&10&1\end{matrix}\right]}\\ \\ \hspace{6.52cm}\mathbf{=[4\hspace{0.2cm}11\hspace{0.2cm}22\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{A_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[4\hspace{0.2cm}11\hspace{0.2cm}22]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5a95d2bfb9008e3add501afa221e89bf_l3.png)
For coordinate B[0 4 2], the newly Scaled coordinate would be B3:
![Rendered by QuickLaTeX.com \mathbf{B_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=B[0\hspace{0.2cm}4\hspace{0.2cm}2\hspace{0.2cm}1]*\left[\begin{matrix}2&4&2&0\\0&1&0&0\\0&0&3&0\\4&11&10&1\end{matrix}\right]}\\ \hspace{6.52cm}\mathbf{=[4\hspace{0.2cm}15\hspace{0.2cm}16\hspace{0.2cm}1]} \\ \hspace{4.15cm}\mathbf{B_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[4\hspace{0.2cm}15\hspace{0.2cm}16]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b89daa3ed2c21a50dae97c58ecfb35bd_l3.png)
For coordinate C[2 4 0], the newly Scaled coordinate would be C3:
![Rendered by QuickLaTeX.com \mathbf{C_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=C[2\hspace{0.2cm}4\hspace{0.2cm}0\hspace{0.2cm}1]*\left[\begin{matrix}2&4&2&0\\0&1&0&0\\0&0&3&0\\4&11&10&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[8\hspace{0.2cm}23\hspace{0.2cm}14\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{C_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[8\hspace{0.2cm}23\hspace{0.2cm}14]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-41e3f18379dd82fc64f8434a5416143d_l3.png)
For coordinate D[2 2 4], the newly Scaled coordinate would be D3:
![Rendered by QuickLaTeX.com \mathbf{D_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=D[2\hspace{0.2cm}2\hspace{0.2cm}4\hspace{0.2cm}1]*\left[\begin{matrix}2&4&2&0\\0&1&0&0\\0&0&3&0\\4&11&10&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[8\hspace{0.2cm}21\hspace{0.2cm}26\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{D_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[8\hspace{0.2cm}21\hspace{0.2cm}26]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0cb6c42abe868bab5fb7ae750df76bd5_l3.png)
For coordinate E[2 0 0], the newly Scaled coordinate would be E3:
![Rendered by QuickLaTeX.com \mathbf{E_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=E[2\hspace{0.2cm}0\hspace{0.2cm}0\hspace{0.2cm}1]*\left[\begin{matrix}2&4&2&0\\0&1&0&0\\0&0&3&0\\4&11&10&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[8\hspace{0.2cm}19\hspace{0.2cm}14\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{E_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[8\hspace{0.2cm}19\hspace{0.2cm}14]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0679801d13d09bc3f25479ed63e7652d_l3.png)
For coordinate F[0 0 2], the newly Scaled coordinate would be F3:
![Rendered by QuickLaTeX.com \mathbf{F_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=F[0\hspace{0.2cm}0\hspace{0.2cm}2\hspace{0.2cm}1]*\left[\begin{matrix}2&4&2&0\\0&1&0&0\\0&0&3&0\\4&11&10&1\end{matrix}\right]}\\ \\ \hspace{6.52cm}\mathbf{=[4\hspace{0.2cm}11\hspace{0.2cm}16\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{F_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[4\hspace{0.2cm}11\hspace{0.2cm}16]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d2085357673f277b0ea22f3f072d9ba8_l3.png)
For coordinate G[2 0 2], the newly Scaled coordinate would be G3:
![Rendered by QuickLaTeX.com \mathbf{G_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=G[2\hspace{0.2cm}0\hspace{0.2cm}2\hspace{0.2cm}1]*\left[\begin{matrix}2&4&2&0\\0&1&0&0\\0&0&3&0\\4&11&10&1\end{matrix}\right]}\\ \\ \hspace{6.52cm}\mathbf{=[8\hspace{0.2cm}19\hspace{0.2cm}20\hspace{0.2cm}1]} \\ \hspace{4.15cm}\mathbf{G_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[8\hspace{0.2cm}19\hspace{0.2cm}20]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5cde8e87216fb9789a4a720b9ac2a562_l3.png)
Here, we get our final result in a single shot:

Fig.5
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...