2D Transformation | Rotation of objects

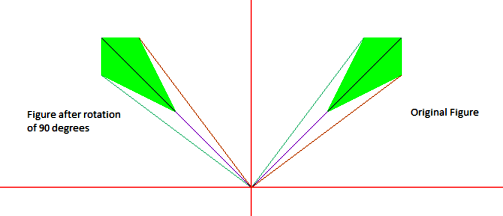
We have to rotate an object by a given angle about a given pivot point and print the new co-ordinates.
Examples: 

Input : {(100, 100), (150, 200), (200, 200), 
         (200, 150)} is to be rotated about 
          (0, 0) by 90 degrees
Output : (-100, 100), (-200, 150), (-200, 200), (-150, 200)

Input : {(100, 100), (100, 200), (200, 200)} 
        is to be rotated about (50, -50) by 
         -45 degrees
Output : (191.421, 20.7107), (262.132, 91.4214), 
         (332.843, 20.7107)

In order to rotate an object we need to rotate each vertex of the figure individually. 
On rotating a point P(x, y) by an angle A about the origin we get a point P'(x’, y’). The values of x’ and y’ can be calculated as follows:-

We know that, 
x = rcosB, y = rsinB
x’ = rcos(A+B) = r(cosAcosB – sinAsinB) = rcosBcosA – rsinBsinA = xcosA – ysinA
y’ = rsin(A+B) = r(sinAcosB + cosAsinB) = rcosBsinA + rsinBcosA = xsinA + ycosA
Rotational Matrix Equation:-

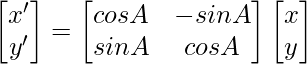
CPP

// C++ program to rotate an object by
// a given angle about a given point
#include <iostream>
#include <math.h>
using namespace std;

// Using macros to convert degree to radian
// and call sin() and cos() as these functions
// take input in radians
#define SIN(x) sin(x * 3.141592653589 / 180)
#define COS(x) cos(x * 3.141592653589 / 180)

// To rotate an object given as order set of points in a[]
// (x_pivot, y_pivot)
void rotate(float a[][2], int n, int x_pivot, int y_pivot,
            int angle)
{
    int i = 0;
    while (i < n) {
        // Shifting the pivot point to the origin
        // and the given points accordingly
        int x_shifted = a[i][0] - x_pivot;
        int y_shifted = a[i][1] - y_pivot;

        // Calculating the rotated point co-ordinates
        // and shifting it back
        a[i][0] = x_pivot
                  + (x_shifted * COS(angle)
                     - y_shifted * SIN(angle));
        a[i][1] = y_pivot
                  + (x_shifted * SIN(angle)
                     + y_shifted * COS(angle));
        cout << "(" << a[i][0] << ", " << a[i][1] << ") ";
        i++;
    }
}

// Driver Code
int main()
{
    // 1st Example
    // The following figure is to be
    // rotated about (0, 0) by 90 degrees
    int size1 = 4; // No. of vertices
    // Vertex co-ordinates must be in order
    float points_list1[][2] = { { 100, 100 },
                                { 150, 200 },
                                { 200, 200 },
                                { 200, 150 } };
    rotate(points_list1, size1, 0, 0, 90);

    // 2nd Example
    // The following figure is to be
    // rotated about (50, -50) by -45 degrees
    /*int size2 = 3;//No. of vertices
    float points_list2[][2] = {{100, 100}, {100, 200},
                                {200, 200}};
    rotate(points_list2, size2, 50, -50, -45);*/
    return 0;
}

Java

// Java program to rotate an object by
// a given angle about a given point
public class rotation {

  static void rotate(double a[][], int n, int x_pivot,
                     int y_pivot, int angle)
  {
    int i = 0;
    while (i < n)
    {

      // Shifting the pivot point to the origin
      // and the given points accordingly
      int x_shifted = (int)a[i][0] - x_pivot;
      int y_shifted = (int)a[i][1] - y_pivot;

      // Calculating the rotated point co-ordinates
      // and shifting it back
      double x = Math.toRadians(angle);
      a[i][0] = x_pivot
        + (x_shifted * Math.cos(x)
           - y_shifted * Math.sin(x));
      a[i][1] = y_pivot
        + (x_shifted * Math.sin(x)
           + y_shifted * Math.cos(x));
      System.out.printf("(%f, %f) ", a[i][0],
                        a[i][1]);
      i++;
    }
  }

  // Driver Code
  public static void main(String[] args)
  {
    // 1st Example
    // The following figure is to be
    // rotated about (0, 0) by 90 degrees
    int size1 = 4; // No. of vertices

    // Vertex co-ordinates must be in order
    double points_list1[][] = { { 100, 100 },
                               { 150, 200 },
                               { 200, 200 },
                               { 200, 150 } };
    rotate(points_list1, size1, 0, 0, 90);

    // 2nd Example
    // The following figure is to be
    // rotated about (50, -50) by -45 degrees
    /*int size2 = 3;//No. of vertices
        double points_list2[][2] = {{100, 100}, {100, 200},
                                    {200, 200}};
        rotate(points_list2, size2, 50, -50, -45);*/
  }
}

// This code is contributed by karandeep1234

Python3

# Python3 program to rotate an object by
# a given angle about a given point
import math

SIN=lambda x: int(math.sin(x * 3.141592653589 / 180))
COS=lambda x: int(math.cos(x * 3.141592653589 / 180))

# To rotate an object
def rotate(a, n, x_pivot, y_pivot, angle):
    i = 0
    while (i < n) :
        # Shifting the pivot point to the origin
        # and the given points accordingly
        x_shifted = a[i][0] - x_pivot
        y_shifted = a[i][1] - y_pivot

        # Calculating the rotated point co-ordinates
        # and shifting it back
        a[i][0] = x_pivot + (x_shifted * COS(angle) - y_shifted * SIN(angle))
        a[i][1] = y_pivot + (x_shifted * SIN(angle) + y_shifted * COS(angle))
        print("({}, {}) ".format(a[i][0], a[i][1]),end=" ")
        i+=1



# Driver Code
if __name__=='__main__':
    # 1st Example
    # The following figure is to be
    # rotated about (0, 0) by 90 degrees
    size1 = 4 # No. of vertices

    # Vertex co-ordinates must be in order
    points_list1 = [[ 100, 100],
                    [ 150, 200],
                    [ 200, 200],
                    [ 200, 150],]
    rotate(points_list1, size1, 0, 0, 90)

    # 2nd Example
    # The following figure is to be
    # rotated about (50, -50) by -45 degrees
    # size2 = 3#No. of vertices
    # points_list2 = [[100, 100],
    #                     [100, 200],
    #                     [200, 200]]
    # rotate(points_list2, size2, 50, -50, -45)

Javascript

// Javascript program to rotate an object by
// a given angle about a given point
const SIN = (x) => Math.sin(x * Math.PI / 180);
const COS = (x) => Math.cos(x * Math.PI / 180);

function rotate(a, n, x_pivot, y_pivot, angle) {
  let i = 0;
  while (i < n) {
    // Shifting the pivot point to the origin
    // and the given points accordingly
    const x_shifted = a[i][0] - x_pivot;
    const y_shifted = a[i][1] - y_pivot;

    // Calculating the rotated point co-ordinates
    // and shifting it back
    a[i][0] = x_pivot + (x_shifted * COS(angle) - y_shifted * SIN(angle));
    a[i][1] = y_pivot + (x_shifted * SIN(angle) + y_shifted * COS(angle));
    console.log(`(${a[i][0]}, ${a[i][1]}) `);
    i++;
  }
}

// Driver Code
// 1st Example
// The following figure is to be
// rotated about (0, 0) by 90 degrees
const size1 = 4; // No. of vertices

// Vertex co-ordinates must be in order
const points_list1 = [[ 100, 100],
                      [ 150, 200],
                      [ 200, 200],
                      [ 200, 150],];
rotate(points_list1, size1, 0, 0, 90);

// 2nd Example
// The following figure is to be
// rotated about (50, -50) by -45 degrees
// const size2 = 3; // No. of vertices
// const points_list2 = [[100, 100],
//                       [100, 200],
//                       [200, 200]];
// rotate(points_list2, size2, 50, -50, -45);

C#

// C# Program to rotate an object by
// a given angle about a given point
using System;

class rotation
{
    // Function to rotate the given points
    // about the pivot point by angle
    static void rotate(double[,] a, int n,
                       int x_pivot, int y_pivot, int angle)
    {
        int i = 0;
        while (i < n)
        {
            // Shifting the pivot point to the origin
            // and the given points accordingly
            int x_shifted = (int)a[i, 0] - x_pivot;
            int y_shifted = (int)a[i, 1] - y_pivot;

            // Calculating the rotated point co-ordinates
            // and shifting it back
            double x = Math.PI * angle / 180.0;
            a[i, 0] = x_pivot + (x_shifted *
                                   Math.Cos(x) - y_shifted *
                                   Math.Sin(x));
            a[i, 1] = y_pivot + (x_shifted *
                                   Math.Sin(x) + y_shifted *
                                   Math.Cos(x));
            Console.Write("({0}, {1}) ",
                          a[i, 0], a[i, 1]);
            i++;
        }
    }

    // Driver Code
    public static void Main(String[] args)
    {
        // 1st Example
        // The following figure is to be
        // rotated about (0, 0) by 90 degrees
        int size1 = 4; // No. of vertices

        // Vertex co-ordinates must be in order
        double[,] points_list1 = { { 100, 100 },
                               { 150, 200 },
                               { 200, 200 },
                               { 200, 150 } };
        rotate(points_list1, size1, 0, 0, 90);

        // 2nd Example
        // The following figure is to be
        // rotated about (50, -50) by -45 degrees
        /*int size2 = 3;//No. of vertices
        double[,] points_list2 = { { 100, 100 },
                                  { 100, 200 },
                                  { 200, 200 } };
        rotate(points_list2, size2, 50, -50, -45);*/
    }
}

Output: 

(-100, 100), (-200, 150), (-200, 200), (-150, 200)

Time Complexity: O(N)
Auxiliary Space: O(1) 
References: Rotation matrix

This article is contributed by Nabaneet Roy. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.