Bresenham’s circle drawing algorithm
Last Updated :
20 Mar, 2024
It is not easy to display a continuous smooth arc on the computer screen as our computer screen is made of pixels organized in matrix form. So, to draw a circle on a computer screen we should always choose the nearest pixels from a printed pixel so as they could form an arc. There are two algorithm to do this:
- Mid-Point circle drawing algorithm
- Bresenham’s circle drawing algorithm
We have already discussed the Mid-Point circle drawing algorithm in our previous post.In this post we will discuss about the Bresenham’s circle drawing algorithm.
Both of these algorithms uses the key feature of circle that it is highly symmetric. So, for whole 360 degree of circle we will divide it in 8-parts each octant of 45 degree. In order to do that we will use Bresenham’s Circle Algorithm for calculation of the locations of the pixels in the first octant of 45 degrees. It assumes that the circle is centered on the origin. So for every pixel (x, y) it calculates, we draw a pixel in each of the 8 octants of the circle as shown below :
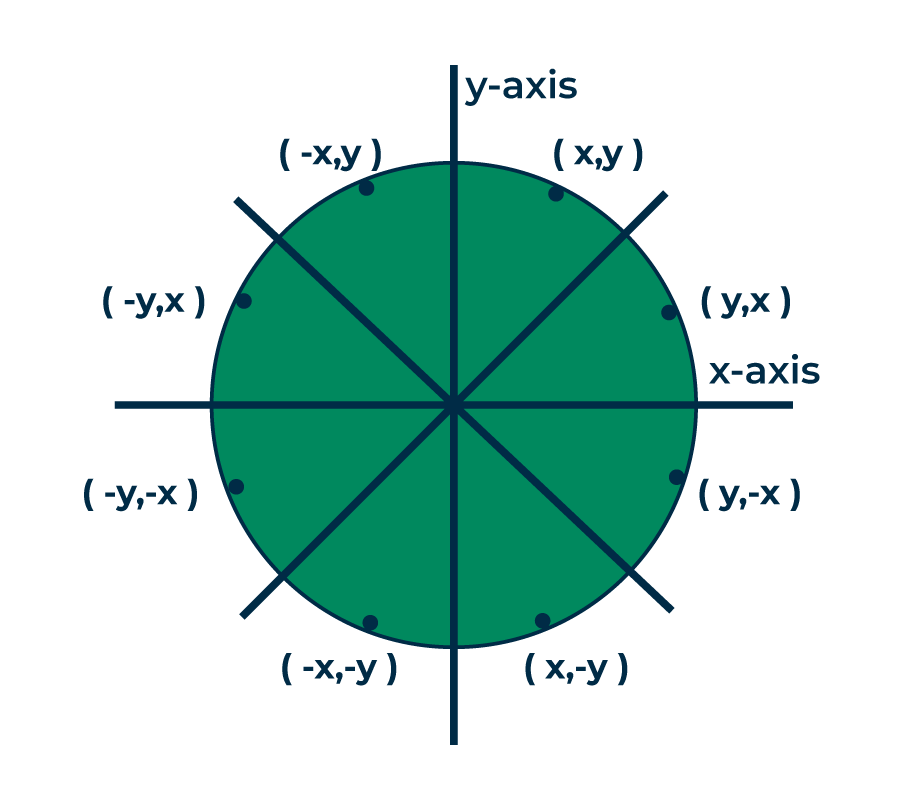
For a pixel (x,y), all possible pixels in 8 octants
Now, we will see how to calculate the next pixel location from a previously known pixel location (x, y). In Bresenham’s algorithm at any point (x, y) we have two option either to choose the next pixel in the east i.e. (x+1, y) or in the south east i.e. (x+1, y-1).
And this can be decided by using the decision parameter d as:
- If d > 0, then (x+1, y-1) is to be chosen as the next pixel as it will be closer to the arc.
- else (x+1, y) is to be chosen as next pixel.
Now to draw the circle for a given radius ‘r’ and centre (xc, yc) We will start from (0, r) and move in first quadrant till x=y (i.e. 45 degree). We should start from listed initial condition:
d = 3 - (2 * r)
x = 0
y = r
Now for each pixel, we will do the following operations:
- Set initial values of (xc, yc) and (x, y)
Set decision parameter d to d = 3 – (2 * r).
- call drawCircle(int xc, int yc, int x, int y) function.
- Repeat steps 5 to 8 until x < = y
- Increment value of x.
- If d < 0, set d = d + (4*x) + 6
- Else, set d = d + 4 * (x – y) + 10 and decrement y by 1.
- call drawCircle(int xc, int yc, int x, int y) function
drawCircle() function:
CPP
// function to draw all other 7 pixels
// present at symmetric position
drawCircle(int xc, int yc, int x, int y)
{
putpixel(xc+x, yc+y, RED);
putpixel(xc-x, yc+y, RED);
putpixel(xc+x, yc-y, RED);
putpixel(xc-x, yc-y, RED);
putpixel(xc+y, yc+x, RED);
putpixel(xc-y, yc+x, RED);
putpixel(xc+y, yc-x, RED);
putpixel(xc-y, yc-x, RED);
}
Below is C implementation of above approach.
CPP
// C-program for circle drawing
// using Bresenham’s Algorithm
// in computer-graphics
#include <stdio.h>
#include <dos.h>
#include <graphics.h>
// Function to put pixels
// at subsequence points
void drawCircle(int xc, int yc, int x, int y)
{
putpixel(xc+x, yc+y, RED);
putpixel(xc-x, yc+y, RED);
putpixel(xc+x, yc-y, RED);
putpixel(xc-x, yc-y, RED);
putpixel(xc+y, yc+x, RED);
putpixel(xc-y, yc+x, RED);
putpixel(xc+y, yc-x, RED);
putpixel(xc-y, yc-x, RED);
}
// Function for circle-generation
// using Bresenham's algorithm
void circleBres(int xc, int yc, int r)
{
int x = 0, y = r;
int d = 3 - 2 * r;
drawCircle(xc, yc, x, y);
while (y >= x)
{
// for each pixel we will
// draw all eight pixels
x++;
// check for decision parameter
// and correspondingly
// update d, x, y
if (d > 0)
{
y--;
d = d + 4 * (x - y) + 10;
}
else
d = d + 4 * x + 6;
drawCircle(xc, yc, x, y);
delay(50);
}
}
// Driver code
int main()
{
int xc = 50, yc = 50, r = 30;
int gd = DETECT, gm;
initgraph(&gd, &gm, ""); // initialize graph
circleBres(xc, yc, r); // function call
return 0;
}
Output:

Advantages
- It is a simple algorithm.
- It can be implemented easily
- It is totally based on the equation of circle i.e. x2 +y2 =r2
Disadvantages
- There is a problem of accuracy while generating points.
- This algorithm is not suitable for complex and high graphic images.
Share your thoughts in the comments
Please Login to comment...