Computer Graphics – 3D Translation Transformation
3-D Transformation :
3-D Transformation is the process of manipulating the view of a three-D object with respect to its original position by modifying its physical attributes through various methods of transformation like Translation, Scaling, Rotation, Shear, etc.
Properties of 3-D Transformation :
- Lines are preserved,
- Parallelism is preserved,
- Proportional distances are preserved.
Types of Transformations :
- Translation
- Scaling
- Rotation
- Shear
- Reflection
Translation :
It is the process of changing the relative location of a 3-D object with respect to the original position by changing its coordinates. Translation transformation matrix in the 3-D image is shown as –
![\\ \newline\hspace{4.48cm} \Large \mathbf{ T[x, y, z]= \left [ \begin{matrix} 1 &0&0& 0\\ 0 & 1&0&0&\\ 0 & 0&1&0\\ D_x&D_y&D_z&1\\ \end{matrix}\right]} \newline \hspace{3.08cm}\\\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c4e57a9cf989d2670e609fde1b77df21_l3.png "Rendered by QuickLaTeX.com")
Where Dx, Dy, Dz are the Translation distances, let a point in 3D space is P(x, y, z) over which we want to apply Translation Transformation operation and we are given with translation distance [Dx, Dy, Dz] So, new position of the point after applying translation operation would be –
![\, \hspace{4.5cm} \textbf{P'[x', y', z', 1] = P[x, y, z, 1].T[x, y, z]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0c17a1ad7ec023ca498efd90cb57ae02_l3.png "Rendered by QuickLaTeX.com")
Problem : Perform translation transformation on the following figure where the given translation distances are Dx = 2, Dy = 4, Dz = 6.
Solution : On applying Translation Transformation we get corresponding points –
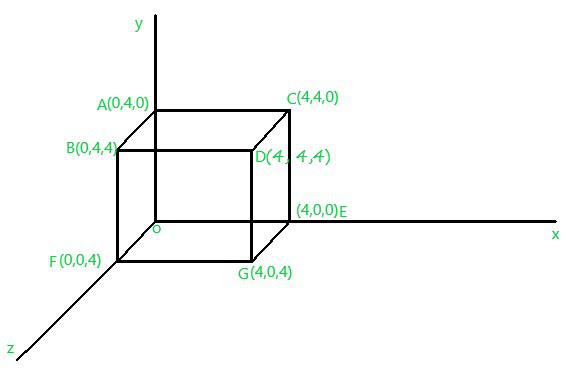
Fig.1
![\large \mathbf{ O'[x, y, z, 1]= [0\, 0\, 0\, 1]\left [ \begin{matrix} 1&0&0&0\\ 0&1&0&0\\ 0&0&1&0\\ 2&4&6&1\\ \end{matrix}\right]=[2\, 4\, 6\, 1]}\\\\ \hspace{4cm}\mathbf{A'[x, y, z, 1]= [0\, 4\, 0\, 1]\left [ \begin{matrix} 1&0&0&0\\ 0&1&0&0\\ 0&0&1&0\\ 2&4&6&1\\ \end{matrix}\right]=[2\, 8\, 6\, 1]}\\\\ \hspace{4cm} \mathbf{B'[x, y, z, 1]= [0\, 4\, 4\, 1]\left [ \begin{matrix} 1&0&0&0\\ 0&1&0&0\\ 0&0&1&0\\ 2&4&6&1\\ \end{matrix}\right]=[2\, 8\, 10\, 1]}\\\\ \hspace{4cm} \mathbf{C'[x, y, z, 1]= [4\, 4\, 0\, 1]\left [ \begin{matrix} 1&0&0&0\\ 0&1&0&0\\ 0&0&1&0\\ 2&4&6&1\\ \end{matrix}\right]=[6\, 8\, 6\, 1]}\\\\ \hspace{4cm} \mathbf{D'[x, y, z, 1]= [4\, 4\, 4\, 1]\left [ \begin{matrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 2 & 4 & 6 & 1\\ \end{matrix}\right]=[6\, 8\, 10\, 1]}\\\\ \hspace{4cm} \mathbf{E'[x, y, z, 1]= [4\, 0\, 0\, 1]\left [ \begin{matrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 2 & 4 & 6 & 1\\ \end{matrix}\right]=[6\, 4\, 6\, 1]}\\\\ \hspace{4cm}\mathbf{ F'[x, y, z, 1]= [0\, 0\, 4\, 1]\left [ \begin{matrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 2 & 4 & 6 & 1\\ \end{matrix}\right]=[2\, 4\, 10\, 1]}\\\\ \hspace{4cm} \mathbf{G'[x, y, z, 1]= [4\, 0\, 4\, 1]\left [ \begin{matrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 2 & 4 & 6 & 1\\ \end{matrix}\right]=[6\, 4\, 10\, 1]}\\\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f0ea962e049f6992169dba8ea1766439_l3.png "Rendered by QuickLaTeX.com")
After performing translation transformation over the Fig.1, it will look like as below –
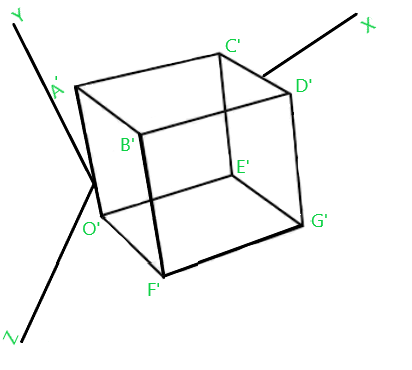
Fig.2
.png)