Natural Numbers are all positive integers from 1 to infinity and are a component of the number system. Natural numbers are also called counting numbers because they are used for counting of various things.

Illustration of Natural Numbers
Let’s learn more about natural numbers, their properties, and examples in detail in this article.
What are Natural Numbers?
Natural numbers or counting numbers are those integers that begin with 1 and go up to infinity.
Only positive integers, such as 1, 2, 3, 4, 5, 6, etc., are included in the set of natural numbers. Natural numbers start from 1 and go up to ∞.
Set of Natural Numbers
In mathematics, the set of natural numbers is expressed as 1, 2, 3, … The set of natural numbers is represented by the symbol N. N = {1, 2, 3, 4, 5, … ∞}. A collection of elements is referred to as a set (numbers in this context). The smallest element in N is 1, and the next element in terms of 1 and N for any element in N. 2 is 1 greater than 1, 3 is 1 greater than 2, and so on. The below table explains the different set forms of natural numbers.
|
Set Form
|
Explanation
|
| Statement Form |
N = Set of numbers generated from 1. |
| Roaster Form |
N = {1, 2, 3, 4, 5, 6, …} |
| Set-builder Form |
N = {x: x is a positive integer starting from 1} |
Natural numbers are the subset of whole numbers, and whole numbers are the subset of integers. Similarly, integers are the subset of real numbers. The below-given diagram explains the relationship w.r.t. the sets of natural numbers, whole numbers, integers, and real numbers.
Types of Natural Numbers
Odd natural numbers
Odd natural numbers are integers greater than zero that cannot be divided evenly by 2, resulting in a remainder of 1 when divided by 2. Examples of odd natural numbers include 1, 3, 5, 7, 9, 11, and so on.
Even natural numbers
Even natural numbers are whole numbers that are divisible by 2 without leaving a remainder. In other words, they are integers greater than zero that can be expressed in the form 2n, where n is an integer. Examples of even natural numbers include 2, 4, 6, 8, 10, and so on.
Natural Numbers from 1 to 100
As Natural Numbers are also called counting numbers, thus natural numbers from 1 to 100 are:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100.
Does 0 belong to Natural numbers?
Natural numbers are counting numbers that start from 1 and go till ∞ and every successor is greater than its predecessor. Thus, 0 is not a natural number. The number 0 precisely belongs to the Whole number.
Natural Numbers and Whole Numbers
The set of whole numbers is identical to the set of natural numbers, with the exception that it includes a 0 as an extra number.
W = {0, 1, 2, 3, 4, 5, …} and N = {1, 2, 3, 4, 5, …}

Difference Between Natural Numbers and Whole Numbers
Let’s discuss the differences between natural numbers and whole numbers.
|
Natural Numbers Vs Whole Numbers
|
|
Natural Numbers
|
Whole Numbers
|
| Smallest natural number is 1. |
Smallest whole number is 0. |
| All natural numbers are whole numbers. |
All whole numbers are not natural numbers. |
| Representation of the set of natural numbers is N = {1, 2, 3, 4, …} |
Representation of the set of whole numbers is W = {0, 1, 2, 3, …} |
Natural Numbers on Number Line
Natural numbers are represented by all positive integers or integers on the right-hand side of 0, whereas whole numbers are represented by all positive integers plus zero.
Here is how we represent natural numbers and whole numbers on the number line:
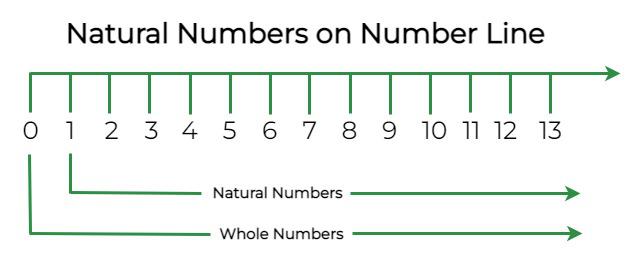
Representation of Natural Numbers on Number Line
Properties of Natural Numbers
All the natural numbers have these properties in common :
- Closure property
- Commutative property
- Associative property
- Distributive property
Let’s learn about these properties in the table below.
| Property |
Description |
Example |
| Closure Property |
| Addition Closure |
Sum of any two natural numbers is a natural number. |
3 + 2 = 5, 9 + 8 = 17 |
| Multiplication Closure |
Product of any two natural numbers is a natural number. |
2 × 4 = 8, 7 × 8 = 56 |
| Associative Property |
| Associative Property of Addition |
Grouping of numbers does not change the sum. |
1 + (3 + 5) = 9, (1 + 3) + 5 = 9 |
| Associative Property of Multiplication |
Grouping of numbers does not change the product. |
2 × (2 × 1) = 4, (2 × 2) × 1 = 4 |
| Commutative Property |
| Commutative Property of Addition |
Order of numbers does not change the sum. |
4 + 5 = 9, 5 + 4 = 9 |
| Commutative Property of Multiplication |
Order of numbers does not change the product. |
3 × 2 = 6, 2 × 3 = 6 |
| Distributive Property |
| Multiplication over Addition |
Distributing multiplication over addition. |
a(b + c) = ab + ac |
| Multiplication over Subtraction |
Distributing multiplication over subtraction. |
a(b – c) = ab – ac |
Note:
- Subtraction and Division may not result in a natural number.
- Associative Property does not hold true for subtraction and division.
Operations With Natural Numbers
We can add, subtract, multiply, and divide the natural numbers together but the result in the subtraction and division is not always a natural number.
Let’s understand the operations on natural numbers:
| Operation |
Description |
Symbol |
Examples |
| Addition |
Combines two or more numbers to find their total. |
+ |
3 + 4 = 7, 11 + 17 = 28 |
| Subtraction |
Finds the difference between two natural numbers; can result in natural or non-natural numbers. |
– |
5 – 3 = 2, 17 – 21 = -4 |
| Multiplication |
Finds the value of repeated addition. |
× or * |
3 × 4 = 12, 7 × 11 = 77 |
| Division |
Divides the number into equal parts; may result in a quotient and a remainder. |
÷ or / |
12 ÷ 3 = 4, 22 ÷ 11 = 2 |
| Exponentiation |
Raises a number to a certain power. |
^ |
23 = 8 |
| Square Root |
The value that, when multiplied by itself, gives the original number. |
√ |
√25 = 5 |
| Factorial |
The product of all positive integers up to and including that number. |
! |
5! = 120 |
Sum of First n Natural Numbers
Sum of first n natural numbers is given by
S = n(n+1)/2
where n is the number of terms taken into consideration.
Mean of First n Natural Numbers
As mean is defined as the ratio of the sum of observations to the number of total observations.
Mean Formula for the first n terms of natural number :
Mean = S/n = (n+1)/2
where,
- S is Sum of all Observations
- n is Number of Terms Taken into Consideration
Sum of Square of First n Natural Numbers
Sum of square of first n natural numbers is given as follows:
S = n(n + 1)(2n + 1)/6
where,
- n is Number Taken into Consideration
Related Articles,
Examples of Natural Numbers
Let’s solve some example problems on Natural Numbers.
Example 1: Identify the natural numbers among the given numbers:
23, 98, 0, -98, 12.7, 11/7, 3.
Solution:
Since negative numbers, 0, decimals, and fractions are not a part of natural numbers.
Therefore, 0, -98, 12.7, and 11/7 are not natural numbers.
Thus, natural numbers are 23, 98, and 3.
Example 2: Prove distributive law of multiplication over addition with an example.
Solution:
Distributive law of multiplication over addition states: a(b + c) = ab + ac
For example, 4(10 + 20), here 4, 10, and 20 are all natural numbers and hence must follow distributive law
4(10 + 20) = 4 × 10 + 4 × 20
4 × 30 = 40 + 80
120 = 120
Hence, proved.
Example 3: Prove distributive law of multiplication over subtraction with an example.
Solution:
Distributive law of multiplication over addition states: a(b – c) = ab – ac.
For example, 7(3 – 6), here 7, 3, and 6 are all natural numbers and hence must follow the distributive law. Therefore,
7(3 – 6) = 7 × 3 – 7 × 6
7 × -3 = 21 + 42
-21 = -21
Hence, proved.
Example 4: List first 10 natural numbers.
Solution:
1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 are the first ten natural numbers.
Practice Questions on Natural Numbers
Various practice question on Natural Numbers are,
Q1: What is Smallest Natural Number?
Q2: What is Biggest Natural Number?
Q3: Simplify, 17(13 – 16)
Q4: Simplify, 11(9 – 2)
Natural Numbers- FAQs
What is Natural Number Definition in Math?
Number used for counting such as 1, 2, 3, 4, 5, . . . so on to infinity, are called natural numbers and any element from this collection is a natural number.
Is 0 a Natural Number?
No, 0 is not a part of natural numbers. 0 is a part of whole numbers, and this is the major difference between whole numbers and natural numbers.
Which is Smallest Natural Number?
Smallest natural number is 1. Natural numbers begin at 1 and go up to infinity. Therefore, the smallest natural number is 1.
How many Natural Numbers are there?
There are infinite natural numbers.
Are Natural Numbers Whole Numbers?
Yes, as set of natural number is subset of the whole number or we can say whole number are natural number with 0. Thus all the natral number are whole number.
Every Whole Number is a Natural Number. True or False?
False. Every whole number is not a natural number as 0 is involved in whole numbers but not in natural numbers. Therefore, the assertion is wrong.
How many Natural Numbers are there between 1 and 100?
As natural number are 1, 2, 3, 4, 5, . . . so on,
Thus, there are exactly 100 natural number till number 100, but as we don’t have to include the 1 and 100.
Thus, there are 100 – 2 = 98, natural number in between 1 and 100.
What is Sum of First n Natural Numbers?
Formula for the sum of first n natural numbers is:
S = n (n + 1)/2
What is Sum of First 10 Natural Numbers?
1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 are the first ten natural numbers. Therefore, the sum of the first 10 natural numbers will be 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55.
Share your thoughts in the comments
Please Login to comment...