Two Clique Problem (Check if Graph can be divided in two Cliques)

A Clique is a subgraph of graph such that all vertices in subgraph are completely connected with each other. Given a Graph, find if it can be divided into two Cliques.

Examples:

Input : G[][] =   {{0, 1, 1, 0, 0},
                  {1, 0, 1, 1, 0},
                  {1, 1, 0, 0, 0},
                  {0, 1, 0, 0, 1},
                  {0, 0, 0, 1, 0}};
Output : Yes

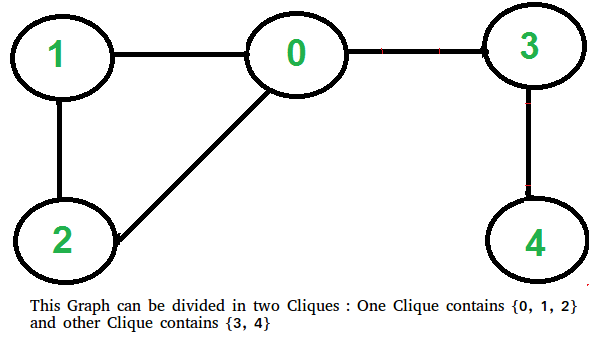
This problem looks tricky at first, but has a simple and interesting solution. A graph can be divided in two cliques if its complement graph is Bipartitite. So below are two steps to find if graph can be divided in two Cliques or not. 

• Find the complement of Graph. Below is the complement graph is above shown graph. In complement, all original edges are removed. And the vertices which did not have an edge between them, now have an edge connecting them. 

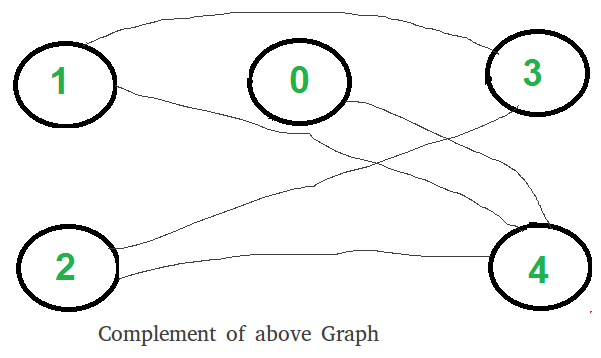
• Return true if complement is Bipartite, else false. The above shown graph is Bipartite. Checking whether a Graph is Bipartite or no is discussed here.

How does this work?
If complement is Bipartite, then graph can be divided into two sets U and V such that there is no edge connecting to vertices of same set. This means in original graph, these sets U and V are completely connected. Hence original graph could be divided in two Cliques.

Implementation:
Below is the implementation of above steps. 

C++

// C++ program to find out whether a given graph can be
// converted to two Cliques or not.
#include <bits/stdc++.h>
using namespace std;

const int V = 5;

// This function returns true if subgraph reachable from
// src is Bipartite or not.
bool isBipartiteUtil(int G[][V], int src, int colorArr[])
{
    colorArr[src] = 1;

    // Create a queue (FIFO) of vertex numbers and enqueue
    // source vertex for BFS traversal
    queue <int> q;
    q.push(src);

    // Run while there are vertices in queue (Similar to BFS)
    while (!q.empty())
    {
        // Dequeue a vertex from queue
        int u = q.front();
        q.pop();

        // Find all non-colored adjacent vertices
        for (int v = 0; v < V; ++v)
        {
            // An edge from u to v exists and destination
            // v is not colored
            if (G[u][v] && colorArr[v] == -1)
            {
                // Assign alternate color to this adjacent
                // v of u
                colorArr[v] = 1 - colorArr[u];
                q.push(v);
            }

            // An edge from u to v exists and destination
            // v is colored with same color as u
            else if (G[u][v] && colorArr[v] == colorArr[u])
                return false;
        }
    }

    // If we reach here, then all adjacent vertices can
    // be colored with alternate color
    return true;
}

// Returns true if a Graph G[][] is Bipartite or not. Note
// that G may not be connected.
bool isBipartite(int G[][V])
{
    // Create a color array to store colors assigned
    // to all vertices. Vertex number is used as index in
    // this array. The value '-1' of  colorArr[i]
    // is used to indicate that no color is assigned to
    // vertex 'i'.  The value 1 is used to indicate first
    // color is assigned and value 0 indicates
    // second color is assigned.
    int colorArr[V];
    for (int i = 0; i < V; ++i)
        colorArr[i] = -1;

    // One by one check all not yet colored vertices.
    for (int i = 0; i < V; i++)
        if (colorArr[i] == -1)
            if (isBipartiteUtil(G, i, colorArr) == false)
                return false;

    return true;
}

// Returns true if G can be divided into
// two Cliques, else false.
bool canBeDividedinTwoCliques(int G[][V])
{
    // Find complement of G[][]
    // All values are complemented except
    // diagonal ones
    int GC[V][V];
    for (int i=0; i<V; i++)
        for (int j=0; j<V; j++)
             GC[i][j] = (i != j)?  !G[i][j] : 0;

    // Return true if complement is Bipartite
    // else false.
    return  isBipartite(GC);
}

// Driver program to test above function
int main()
{
    int G[][V] = {{0, 1, 1, 1, 0},
        {1, 0, 1, 0, 0},
        {1, 1, 0, 0, 0},
        {0, 1, 0, 0, 1},
        {0, 0, 0, 1, 0}
    };

    canBeDividedinTwoCliques(G) ? cout << "Yes" :
                                  cout << "No";
    return 0;
}

Java

// Java program to find out whether a given graph can be
// converted to two Cliques or not.
import java.util.ArrayDeque;
import java.util.Deque;
class GFG {
static int V = 5;

// This function returns true if subgraph reachable from
// src is Bipartite or not.
static boolean isBipartiteUtil(int G[][], int src, int colorArr[])
{
    colorArr[src] = 1;

    // Create a queue (FIFO) of vertex numbers and enqueue
    // source vertex for BFS traversal
    Deque <Integer> q = new ArrayDeque<>();
    q.push(src);

    // Run while there are vertices in queue (Similar to BFS)
    while (!q.isEmpty())
    {
        // Dequeue a vertex from queue
        int u = q.peek();
        q.pop();

        // Find all non-colored adjacent vertices
        for (int v = 0; v < V; ++v)
        {
            // An edge from u to v exists and destination
            // v is not colored
            if (G[u][v] == -1 && colorArr[v] == -1)
            {
                // Assign alternate color to this adjacent
                // v of u
                colorArr[v] = 1 - colorArr[u];
                q.push(v);
            }

            // An edge from u to v exists and destination
            // v is colored with same color as u
            else if (G[u][v] == colorArr[u] && colorArr[v] == colorArr[u])
                return false;
        }
    }

    // If we reach here, then all adjacent vertices can
    // be colored with alternate color
    return true;
}

// Returns true if a Graph G[][] is Bipartite or not. Note
// that G may not be connected.
static boolean isBipartite(int G[][])
{
    // Create a color array to store colors assigned
    // to all vertices. Vertex number is used as index in
    // this array. The value '-1' of  colorArr[i]
    // is used to indicate that no color is assigned to
    // vertex 'i'.  The value 1 is used to indicate first
    // color is assigned and value 0 indicates
    // second color is assigned.
    int colorArr[]=new int[V];
    for (int i = 0; i < V; ++i)
        colorArr[i] = -1;

    // One by one check all not yet colored vertices.
    for (int i = 0; i < V; i++)
        if (colorArr[i] == -1)
            if (isBipartiteUtil(G, i, colorArr) == false)
                return false;

    return true;
}

// Returns true if G can be divided into
// two Cliques, else false.
static boolean canBeDividedinTwoCliques(int G[][])
{
    // Find complement of G[][]
    // All values are complemented except
    // diagonal ones
    int GC[][]=new int[V][V];
    for (int i=0; i<V; i++)
        for (int j=0; j<V; j++)
             GC[i][j] = (i != j)?  -GC[i][j] : 0;

    // Return true if complement is Bipartite
    // else false.
    return  isBipartite(GC);
}

// Driver program to test above function
public static void main(String[] args) {
     int G[][] = {{0, 1, 1, 1, 0},
        {1, 0, 1, 0, 0},
        {1, 1, 0, 0, 0},
        {0, 1, 0, 0, 1},
        {0, 0, 0, 1, 0}
    };

    if(canBeDividedinTwoCliques(G))
             System.out.println("Yes");
    else
        System.out.println("No");
    }
}
/* This code contributed by PrinciRaj1992 */

Python3

# Python3 program to find out whether a given
# graph can be converted to two Cliques or not.
from queue import Queue

# This function returns true if subgraph
# reachable from src is Bipartite or not.
def isBipartiteUtil(G, src, colorArr):
    global V
    colorArr[src] = 1

    # Create a queue (FIFO) of vertex numbers
    # and enqueue source vertex for BFS traversal
    q = Queue()
    q.put(src)

    # Run while there are vertices in
    # queue (Similar to BFS)
    while (not q.empty()):

        # Dequeue a vertex from queue
        u = q.get()

        # Find all non-colored adjacent vertices
        for v in range(V):

            # An edge from u to v exists and
            # destination v is not colored
            if (G[u][v] and colorArr[v] == -1):

                # Assign alternate color to this
                # adjacent v of u
                colorArr[v] = 1 - colorArr[u]
                q.put(v)

            # An edge from u to v exists and destination
            # v is colored with same color as u
            elif (G[u][v] and colorArr[v] == colorArr[u]):
                return False

    # If we reach here, then all adjacent
    # vertices can be colored with alternate color
    return True

# Returns true if a Graph G[][] is Bipartite or not.
# Note that G may not be connected.
def isBipartite(G):
    global V

    # Create a color array to store colors assigned
    # to all vertices. Vertex number is used as index
    # in this array. The value '-1' of colorArr[i]
    # is used to indicate that no color is assigned
    # to vertex 'i'. The value 1 is used to indicate
    # first color is assigned and value 0 indicates
    # second color is assigned.
    colorArr = [-1] * V

    # One by one check all not yet
    # colored vertices.
    for i in range(V):
        if (colorArr[i] == -1):
            if (isBipartiteUtil(G, i, colorArr) == False):
                return False

    return True

# Returns true if G can be divided into
# two Cliques, else false.
def canBeDividedinTwoCliques(G):
    global V

    # Find complement of G[][]
    # All values are complemented
    # except diagonal ones
    GC = [[None] * V for i in range(V)]
    for i in range(V):
        for j in range(V):
            GC[i][j] = not G[i][j] if i != j else 0

    # Return true if complement is
    # Bipartite else false.
    return isBipartite(GC)

# Driver Code
V = 5

G = [[0, 1, 1, 1, 0],
     [1, 0, 1, 0, 0],
     [1, 1, 0, 0, 0],
     [0, 1, 0, 0, 1],
     [0, 0, 0, 1, 0]]

if canBeDividedinTwoCliques(G):
    print("Yes")
else:
    print("No")

# This code is contributed by PranchalK

Javascript

<script>

// JavaScript program to find out whether a given graph can be
// converted to two Cliques or not.

const V = 5;

// This function returns true if subgraph reachable from
// src is Bipartite or not.
function isBipartiteUtil(G,src,colorArr)
{
    colorArr[src] = 1;

    // Create a queue (FIFO) of vertex numbers and enqueue
    // source vertex for BFS traversal
    let q = [];
    q.push(src);

    // Run while there are vertices in queue (Similar to BFS)
    while (q.length > 0)
    {
        // Dequeue a vertex from queue
        let u = q.shift();

        // Find all non-colored adjacent vertices
        for (let v = 0; v < V; ++v)
        {
            // An edge from u to v exists and destination
            // v is not colored
            if (G[u][v] && colorArr[v] == -1)
            {
                // Assign alternate color to this adjacent
                // v of u
                colorArr[v] = 1 - colorArr[u];
                q.push(v);
            }

            // An edge from u to v exists and destination
            // v is colored with same color as u
            else if (G[u][v] && colorArr[v] == colorArr[u])
                return false;
        }
    }

    // If we reach here, then all adjacent vertices can
    // be colored with alternate color
    return true;
}

// Returns true if a Graph G[][] is Bipartite or not. Note
// that G may not be connected.
function isBipartite(G)
{
    // Create a color array to store colors assigned
    // to all vertices. Vertex number is used as index in
    // this array. The value '-1' of  colorArr[i]
    // is used to indicate that no color is assigned to
    // vertex 'i'.  The value 1 is used to indicate first
    // color is assigned and value 0 indicates
    // second color is assigned.
    let colorArr = new Array(V);
    for (let i = 0; i < V; ++i)
        colorArr[i] = -1;

    // One by one check all not yet colored vertices.
    for (let i = 0; i < V; i++)
        if (colorArr[i] == -1)
            if (isBipartiteUtil(G, i, colorArr) == false)
                return false;

    return true;
}

// Returns true if G can be divided into
// two Cliques, else false.
function canBeDividedinTwoCliques(G)
{
    // Find complement of G[][]
    // All values are complemented except
    // diagonal ones
    let GC = new Array(V).fill(0).map(()=>new Array(V));
    for (let i=0; i<V; i++)
        for (let j=0; j<V; j++)
             GC[i][j] = (i != j)?  !G[i][j] : 0;

    // Return true if complement is Bipartite
    // else false.
    return  isBipartite(GC);
}

// Driver program to test above function

let G =[[0, 1, 1, 1, 0],
       [1, 0, 1, 0, 0],
       [1, 1, 0, 0, 0],
       [0, 1, 0, 0, 1],
       [0, 0, 0, 1, 0]
    ];

canBeDividedinTwoCliques(G) ? document.write("Yes"):
                                 document.write("No");

// This code is contributed by shinjanpatra

</script>

C#

using System;
using System.Collections.Generic;

class GFG {
    static int V = 5;

    // This function returns true if subgraph reachable from
    // src is Bipartite or not.
    static bool IsBipartiteUtil(int[, ] G, int src,
                                int[] colorArr)
    {
        colorArr[src] = 1;

        // Create a queue (FIFO) of vertex numbers and
        // enqueue source vertex for BFS traversal
        Queue<int> q = new Queue<int>();
        q.Enqueue(src);

        // Run while there are vertices in queue (Similar to
        // BFS)
        while (q.Count > 0) {
            // Dequeue a vertex from queue
            int u = q.Dequeue();

            // Find all non-colored adjacent vertices
            for (int v = 0; v < V; ++v) {
                // An edge from u to v exists and
                // destination v is not colored
                if (G[u, v] == -1 && colorArr[v] == -1) {
                    // Assign alternate color to this
                    // adjacent v of u
                    colorArr[v] = 1 - colorArr[u];
                    q.Enqueue(v);
                }

                // An edge from u to v exists and
                // destination v is colored with same color
                // as u
                else if (G[u, v] == colorArr[u]
                         && colorArr[v] == colorArr[u])
                    return false;
            }
        }

        // If we reach here, then all adjacent vertices can
        // be colored with alternate color
        return true;
    }

    // Returns true if a Graph G[][] is Bipartite or not.
    // Note that G may not be connected.
    static bool IsBipartite(int[, ] G)
    {
        // Create a color array to store colors assigned
        // to all vertices. Vertex number is used as index
        // in this array. The value '-1' of  colorArr[i] is
        // used to indicate that no color is assigned to
        // vertex 'i'.  The value 1 is used to indicate
        // first color is assigned and value 0 indicates
        // second color is assigned.
        int[] colorArr = new int[V];
        for (int i = 0; i < V; ++i)
            colorArr[i] = -1;

        // One by one check all not yet colored vertices.
        for (int i = 0; i < V; i++)
            if (colorArr[i] == -1)
                if (!IsBipartiteUtil(G, i, colorArr))
                    return false;

        return true;
    }

    // Returns true if G can be divided into
    // two Cliques, else false.
    static bool CanBeDividedInTwoCliques(int[, ] G)
    {
        // Find complement of G[][]
        // All values are complemented except
        // diagonal ones

        int[, ] GC = new int[V, V];
        for (int i = 0; i < V; i++)
            for (int j = 0; j < V; j++)
                GC[i, j] = (i != j) ? -GC[i, j] : 0;

        // Return true if complement is Bipartite
        // else false.
        return IsBipartite(GC);
    }

    // Driver program to test above function
    static void Main(string[] args)
    {
        int[, ] G = { { 0, 1, 1, 1, 0 },
                      { 1, 0, 1, 0, 0 },
                      { 1, 1, 0, 0, 0 },
                      { 0, 1, 0, 0, 1 },
                      { 0, 0, 0, 1, 0 } };

        if (CanBeDividedInTwoCliques(G))
            Console.WriteLine("Yes");
        else
            Console.WriteLine("No");
    }
} // this code is contributed by dany

Output : 

Yes

Time complexity : O(V²)

Space complexity : O(V^2),

Reference: 

If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above