Trigonometric ratios of some Specific Angles

Read

Discuss

Trigonometry is all about triangles or to be more precise the relationship between the angles and sides of a triangle (right-angled triangle). In this article, we will be discussing the ratio of sides of a right-angled triangle concerning its acute angle called trigonometric ratios of the angle and find the trigonometric ratios of specific angles: 0°, 30°, 45°, 60°, and 90°.
Consider the following triangle,

The side BA is opposite to the angle ∠BCA so we call BA the opposite side to ∠C and AC is the hypotenuse; the other side BC is the adjacent side to ∠C.

Trigonometric Ratios of angle C

Sine: Sine of ∠C is the ratio of the side opposite to C (BA) to the hypotenuse (AC).

$sin\, C = \frac{BA}{AC}$

Cosine: Cosine of ∠C is the ratio of the side adjacent to C (BC) and the hypotenuse (AC).

$cos\, C = \frac{BC}{AC}$

Tangent: The tangent of ∠C is the ratio between the side opposite (BA) and adjacent to C (BC).

$tan\, C = \frac{BA}{BC}$

Cosecant: Cosecant of ∠C is the reciprocal of sin C therefore it is the ratio of the hypotenuse (AC) to the side opposite to C (BA).

$cosec\, C = \frac{AC}{BA}$

Secant: Secant of ∠C is the reciprocal of cos C therefore it is the ratio of the hypotenuse (AC) to the side adjacent to C (BC).

$sec\, C = \frac{AC}{BC}$

Cotangent: Cotangent of ∠C is the reciprocal of tan C that is the ratio of the side adjacent to C (BC) to the side opposite to C (BA).

$cot\, C = \frac{BC}{BA}$

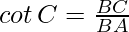
Finding trigonometric ratios for angles 0°, 30°, 45°, 60°, 90°

Considering the length of the hypotenuse AC = a, BC = b and, BA = c.

A. For angles 0° and 90°

If angle A = 0°, the length of the opposite side would be zero and hypotenuse = adjacent side, and if A = 90°, the hypotenuse = opposite side. So, with the help of the above formulas for the trigonometric ratios we get –

if A = 0° $\\ sin A = \frac{BC}{AC} = \frac{b}{a} = 0 \\\quad\\ cos A = \frac{AB}{AC} = \frac{c}{a} =1 \\\quad\\ tan A = \frac{BC}{AB} = \frac{b}{a} = 0 \\\quad\\ cosec A = \frac{AC}{BC} = \frac{a}{b} = not\, defined \\\quad\\ sec A = \frac{AC}{AB} = \frac{a}{c}= 1 \\\quad\\ cot A = \frac{AB}{BC} = \frac{a}{b}= not\, defined \\\quad\\$

if A = 90° $\\ sin A = \frac{BC}{AC} = \frac{b}{a} = 1 \\\quad\\ cos A = \frac{BA}{AC} = \frac{c}{a} = 0 \\\quad\\ tan A = \frac{BC}{BA} = \frac{b}{c} = not\, defined \\\quad\\ cosec A = \frac{AC}{BC} = \frac{b}{a}= 1 \\\quad\\ sec A = \frac{AC}{BA} = \frac{a}{c}= not\, defined \\\quad\\ cot A = \frac{BA}{BC} = 0$

Here some of the trigonometric ratios result as not defined as at the particular angle it is divided by 0 which is undefined.

B. For angles 30° and 60°

Consider an equilateral triangle ABC. Since each angle in an equilateral triangle is 60°, therefore,

∠A = ∠B = ∠C = 60°.

∆ABD is a right triangle, right-angled at D with ∠BAD = 30° and ∠ABD = 60°,

Here ∆ADB and ∆ADC are similar as they are Corresponding parts of Congruent triangles (CPCT).

$In\, \Delta ABD\;,AB=a\,,BD=\frac{a}{2} \\and\,AB^2=BD^2+AD^2\\ \quad\\\implies AD^2=AB^2-BD^2 \\ \quad\\\implies AD^2=a^2-(\frac{a}{2})^2\\ \quad\\ \implies AD^2=a^2-\frac{a^2}{4} \\ \quad\\ \implies AD^2=\frac{3a^2}{4} \\\quad\\ \implies AD= \frac{\sqrt{3} a}{2}$

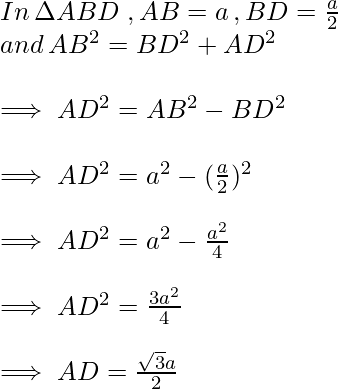
Now we know the values of AB, BD, and AD, So the trigonometric ratios for angle 30° are,

$sin\ 30=\frac{BD}{AB}= \frac{a/2}{a}=\frac{1}{2} \\ \quad\\cos\ 30=\frac{AD}{AB}=\frac{\sqrt{3}a/2}{a} =\frac{\sqrt{3}}{2} \\ \quad\\tan\ 30=\frac{BD}{AD}=\frac{a/2}{\sqrt{3}a/2}=\frac{1}{\sqrt{3}} \\\quad\\cosec\ 30=\frac{AB}{BD}=\frac{a}{a/2}=2 \\\quad\\sec\ 30=\frac{AB}{AD}=\frac{a}{\sqrt{3}a/2} =\frac{2}{\sqrt{3}} \\\quad\\cot\ 30=\frac{AD}{BD}=\frac{\sqrt{3}a/2}{a/2}= \sqrt{3}$

For angle 60°

$sin\ 60=\frac{AD}{AB}= \frac{\sqrt{3}a/2}{a}=\frac{\sqrt{3}}{2} \\ \quad\\cos\ 60=\frac{BD}{AB}=\frac{a/2}{a}=\frac{1}{2} \\\quad\\tan\ 60=\frac{AD}{BD}=\frac{\sqrt{3}a/2}{a/2}=\sqrt{3} \\\quad\\cosec\ 60=\frac{AB}{AD}=\frac{a}{\sqrt{3}a/2}=\frac{2}{\sqrt{3}} \\\quad\\sec=\frac{AB}{BD}=\frac{a}{a/2}=2 \\\quad\\cot\ 60=\frac{BD}{AD}=\frac{a/2}{\sqrt{3}a/2}=\frac{1}{\sqrt{3}}$

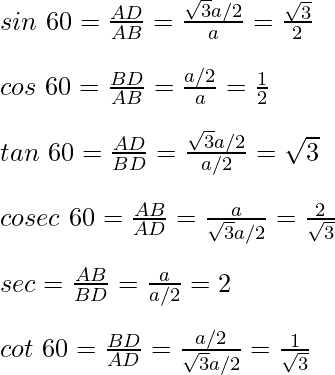
C. For angle 45°

In a right-angled triangle if one angle is 45° then the other angle is also 45° thus, making it an isosceles right-angle triangle.

If the length of side BC = a then length of AB = a and length of AC(hypotenuse) is a√2 using Pythagoras Theorem, then

$sin\ A = \frac{BC}{AC} = \frac{a}{a\sqrt2} = \frac{1}{\sqrt2}\\ \quad\\ cos\ A = \frac{AB}{AC} = \frac{a}{a\sqrt2} = \frac{1}{\sqrt2}\\ \quad\\ tan\ A = \frac{BC}{AB} = \frac{a}{a} = 1\\ \quad\\ cosec\ A = \frac{1}{sin\ A}= \sqrt2\\ \quad\\ sec\ A = \frac{1}{cos\ A} = \sqrt2\\ \quad\\ cot\ A = \frac{1}{tan\ A} = 1\\$

All values

∠A	0°	30°	45°	60°	90°
sin A	0	1/2	1/√2	√3/2	1
cos A	1	√3/2	1/√2	1/2	0
tan A	0	1/√3	1	√3	Not defined
cosec A	Not defined	2	√2	2/√3	1
sec A	1	2/√3	√2	2	Not defined
cot A	Not defined	√3	1	1/√3	0

Whether you're preparing for your first job interview or aiming to upskill in this ever-evolving tech landscape, GeeksforGeeks Courses are your key to success. We provide top-quality content at affordable prices, all geared towards accelerating your growth in a time-bound manner. Join the millions we've already empowered, and we're here to do the same for you. Don't miss out - check it out now!

Last Updated : 24 Jun, 2022