Trigonometric Ratios of Some Specific Angles
Last Updated :
25 Apr, 2024
Trigonometry is all about triangles or to be more precise the relationship between the angles and sides of a triangle (right-angled triangle). In this article, we will be discussing the ratio of sides of a right-angled triangle concerning its acute angle called trigonometric ratios of the angle and find the trigonometric ratios of specific angles: 0°, 30°, 45°, 60°, and 90°.
Consider the following triangle,

The side BA is opposite to the angle ∠BCA so we call BA the opposite side to ∠C and AC is the hypotenuse; the other side BC is the adjacent side to ∠C.
Trigonometric Ratios of Angle C
Sine: Sine of ∠C is the ratio of the side opposite to C (BA) to the hypotenuse (AC).

Cosine: Cosine of ∠C is the ratio of the side adjacent to C (BC) and the hypotenuse (AC).

Tangent: The tangent of ∠C is the ratio between the side opposite (BA) and adjacent to C (BC).

Cosecant: Cosecant of ∠C is the reciprocal of sin C therefore it is the ratio of the hypotenuse (AC) to the side opposite to C (BA).

Secant: Secant of ∠C is the reciprocal of cos C therefore it is the ratio of the hypotenuse (AC) to the side adjacent to C (BC).

Cotangent: Cotangent of ∠C is the reciprocal of tan C that is the ratio of the side adjacent to C (BC) to the side opposite to C (BA).
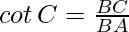
Finding Trigonometric Ratios for Angles 0°, 30°, 45°, 60°, 90°
Considering the length of the hypotenuse AC = a, BC = b and, BA = c.
For angles 0° and 90°
If angle A = 0°, the length of the opposite side would be zero and hypotenuse = adjacent side, and if A = 90°, the hypotenuse = opposite side. So, with the help of the above formulas for the trigonometric ratios we get –
if A = 0° 
if A = 90° 
Here some of the trigonometric ratios result as not defined as at the particular angle it is divided by 0 which is undefined.
For angles 30° and 60°
Consider an equilateral triangle ABC. Since each angle in an equilateral triangle is 60°, therefore,
∠A = ∠B = ∠C = 60°.

∆ABD is a right triangle, right-angled at D with ∠BAD = 30° and ∠ABD = 60°,
Here ∆ADB and ∆ADC are similar as they are Corresponding parts of Congruent triangles (CPCT).
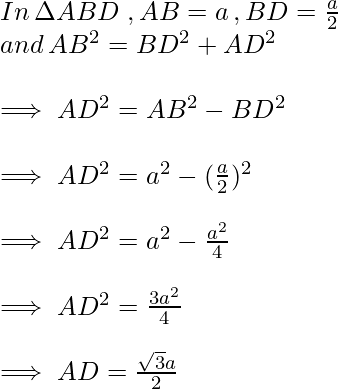
Now we know the values of AB, BD, and AD, So the trigonometric ratios for angle 30° are,

For angle 60°
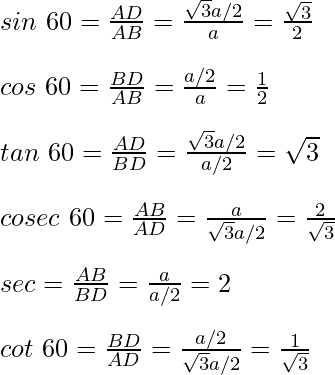
For angle 45°
In a right-angled triangle if one angle is 45° then the other angle is also 45° thus, making it an isosceles right-angle triangle.

If the length of side BC = a then length of AB = a and length of AC(hypotenuse) is a√2 using Pythagoras Theorem, then

All Values of Trigonometric Ratios [Some Specific Angles]
Some of the common values of trigonometric ratios are listed in the following table:
| ∠A | 0° | 30° | 45° | 60° | 90° |
| sin A | 0 | 1/2 | 1/√2 | √3/2 | 1 |
| cos A | 1 | √3/2 | 1/√2 | 1/2 | 0 |
| tan A | 0 | 1/√3 | 1 | √3 | Not defined |
| cosec A | Not defined | 2 | √2 | 2/√3 | 1 |
| sec A | 1 | 2/√3 | √2 | 2 | Not defined |
| cot A | Not defined | √3 | 1 | 1/√3 | 0 |
Related Articles
Share your thoughts in the comments
Please Login to comment...