Applications of various Automata
Last Updated :
09 Mar, 2023
Automata is a machine that can accept the Strings of a Language L over an input alphabet Σ . So far we are familiar with the Types of Automata. Now, let us discuss the expressive power of Automata and further understand its Applications.
Expressive Power of various Automata: The Expressive Power of any machine can be determined from the class or set of Languages accepted by that particular type of Machine. Here is the increasing sequence of expressive power of machines :
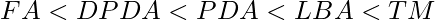
As we can observe that FA is less powerful than any other machine. It is important to note that DFA and NFA are of same power because every NFA can be converted into DFA and every DFA can be converted into NFA . The Turing Machine i.e. TM is more powerful than any other machine
(i) Finite Automata (FA) equivalence:
Finite Automata
≡ PDA with finite Stack
≡ TM with finite tape
≡ TM with unidirectional tape
≡ TM with read only tape
(ii) Pushdown Automata (PDA) equivalence:
PDA ≡ Finite Automata with Stack
(iii) Turing Machine (TM) equivalence:
Turing Machine
≡ PDA with additional Stack
≡ FA with 2 Stacks
The Applications of these Automata are given as follows:
1. Finite Automata (FA) –
- For the designing of lexical analysis of a compiler.
- For recognizing the pattern using regular expressions.
- For the designing of the combination and sequential circuits using Mealy and Moore Machines.
- Used in text editors.
- For the implementation of spell checkers.
- Can be used as a model for learning and decision making.
- Can parse text to extract information and structure data.
2. Push Down Automata (PDA) –
- For designing the parsing phase of a compiler (Syntax Analysis).
- For implementation of stack applications.
- For evaluating the arithmetic expressions.
- For solving the Tower of Hanoi Problem.
- Can be used in software engineering, to verify and validate the correctness of software models.
- Can be used in network protocols, to parse and validate incoming messages and to enforce specific message formats.
- Can be used in cryptography, to implement secure algorithms for encryption and decryption.
- Used in string matching and pattern recognition, to search for specific patterns in input strings.
- Used in XML parsing.
- Used in natural language processing applications like parsing sentences, recognizing parts of speech, and generating syntax trees.
- Used in automatic theorem proving and formal verification.
- Used in formal verification of hardware and software systems.
3. Linear Bounded Automata (LBA) –
- For implementation of genetic programming.
- For constructing syntactic parse trees for semantic analysis of the compiler.
- For recognition of context-sensitive languages.
- Used in game theory to model and analyze interactions between agents.
4. Turing Machine (TM) –
- For solving any recursively enumerable problem.
- For understanding complexity theory.
- For implementation of neural networks.
- For implementation of Robotics Applications.
- For implementation of artificial intelligence.
- Used as a theoretical model to analyze the time and space complexity of algorithms.
- Used in computational biology to model and analyze biological systems.
- Used in artificial intelligence as a model for learning and decision making.
- Used to study the relationship between classical computing and quantum computing.
- Used in digital circuit design to model and verify the behavior of digital circuits.
- Used in human-computer interaction to model and analyze the interaction between humans and computers.
Share your thoughts in the comments
Please Login to comment...