Simple Harmonic Motion is a type of periodic motion that repeats itself after a certain time period. It is seen almost everywhere in real life, for example, a body connected to spring is doing simple harmonic motion. These systems are an important part of our lives and it is essential to understand and study them to be able to model their behaviors. The equations of SHM help us deduce information about the object from the SHM and predict its behavior. Let’s look at how to extract this information from an SHM in detail.
Periodic and Oscillatory Motion
Consider an example of an insect trying to climb up the wall, this insect climbs up to a height and then falls back down again. Notice, that the motion of this insect is repeating itself after some time. This kind of motion is called periodic motion. A periodic motion repeats itself after a certain interval of time. In the figure, some graphs are shown which represent a periodic motion. The graph has a pattern that is repeating, which means that the y-position of the object increases and then decreases periodically.
Periodic and Oscillatory motions may seem the same, but they have a minor difference. Every oscillatory motion is a periodic motion but not vice-versa. Periodic motions just repeat themselves after a certain interval of time, but oscillatory motions move to and fro around a mean position. Simple Harmonic Motion is the simplest type of oscillatory motion.
Simple Harmonic Motion
Simple Harmonic Motion is a kind of periodic motion where the object moves to and fro around its mean position. This motion arises when the force acting on the body is directly proportional to the displacement of the body from its mean position. The time period, in this case, remains constant. The time period is denoted by “T” and the distance of the mean position from the extreme position is called amplitude, it is denoted by A. An oscillating pendulum is an example of Simple Harmonic Motion.
A general equation of SHM is given by,
x(t) = Asin(ωt + φ)
Here, A represents the amplitude and ω represents the angular frequency of the SHM.
Spring Block system and Pendulum system are two examples of the systems around us in real life which perform Simple Harmonic Motion. Under ideal conditions of no frictional and air drag, these systems are able to perform perfect SHMs. Let’s look at both of these systems one by one in detail.
Spring Block System
The figure given below shows a spring-mass system. A spring-mass system consists of a spring of a negligible mass. One end of a spring is attached to a rigid support and the other end carries a block of mass M, this block lies on a frictionless flat surface. For a deformation of length “x” in the spring, the restoring force that is generated in the spring is given by,
F = -kx
Here, k is the spring constant and the negative sign denotes the direction of the restoring force that is always opposite to the deformation caused in the system.

This relation can be combined with Newton’s law,
F = ma = -kx
⇒ a = 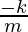 x
x
Comparing this equation with the equation of acceleration in SHM, a = -ω2x,
In this case,
ω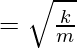
⇒ 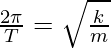
⇒ T = 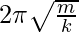
Pendulum
This motion arises when the force acting on the body is directly proportional to the displacement of the body from its mean position. The time period, in this case, remains constant. The time period is denoted by “T” and the distance of the mean position from the extreme position is called amplitude, it is denoted by A. An oscillating pendulum is an example of Simple Harmonic Motion.

The general equation for the displacement(x) of the object at any particular time is given by,
x = A sin (ωt + φ)
Here, ω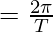 and φ denotes the phase shift.
and φ denotes the phase shift.
Similarly, the equation for the velocity of the object in SHM can be found by differentiating this equation.
v = Aω cos(ωt + φ)
Then, the equation for acceleration becomes,
a = -Aω2 sin(ωt + φ)

Notice in the figure above, that all three values displacement, velocity, and acceleration in SHM have the same time period as SHM, but they have a phase of 90° between each of them.
Sample Problems
Question 1: The equation for the SHM is given below
x(t) = 10cos(t)
Calculate the maximum acceleration and velocity.
Answer:
General equation of SHM is given by,
x(t) = Asin(ωt + φ)
In this case, A = 10, ω = 1
Maximum velocity will be,
v = Aω
⇒ v = (10)(1)
⇒ v = 10 m/s
Maximum acceleration will be,
a = -Aω2
⇒ a = – (10)(1)2
⇒ a = -10 m/s2
Question 2: The equation for the SHM is given below.
x(t) = 20sin(2t)
Calculate the maximum acceleration and velocity.
Answer:
General equation of SHM is given by,
x = A sin (ωt + φ)
In this case, A = 20, ω = 2
Maximum velocity will be,
v = Aω
⇒ v = (20)(2)
⇒ v = 40 m/s
Maximum acceleration will be,
a = -Aω2
⇒ a = – (20)(2)2
⇒ a = -80 m/s2
Question 3: Find the time period of the spring-block system performing SHM. The mass of the block is 25Kg and k = 100N/m.
Answer:
The time period, in this case is given by,
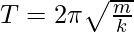
Given:
m =25Kg and k = 100N/m.
Plugging these values into the equation,
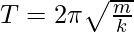
⇒ 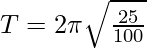
⇒ T = π/2
Question 4: Find the time period of the spring-block system performing SHM. The mass of the block is 100Kg and k = 900N/m.
Answer:
The time period, in this case is given by,
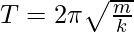
Given:
m =100Kg and k = 900N/m.
Plugging these values into the equation,
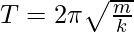
⇒ 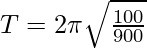
⇒ T = 2π/3
Question 5: The equation for the SHM performed by a pendulum is given below.
x(t) = 10sin(t + 5)
Calculate the time and velocity at t = 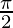
Answer:
General equation of SHM is given by,
x(t) = Asin(ωt + φ)
In this case, A = 10, ω = 1
We know,
ω = 2π/T
Plugging the values into the equation,
ω = 2π/T
⇒ T = 2π/ω
⇒ T = 2π
Equation for velocity will be found by differentiating the given equation,
x(t) = 10sin(t + 5)
⇒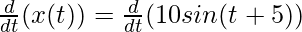
⇒ v(t) = 10cos(t + 5)
At t = 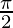
v(t) = 10cos(t + 5)
⇒ v(t) = 10cos(π/2 + 5)
⇒ v(t) = -10sin(5)
Share your thoughts in the comments
Please Login to comment...