Energy in Simple Harmonic Motion
Last Updated :
21 Jul, 2021
Each and every object possesses energy. In a simple harmonic motion, the object goes to the extreme and acquires potential energy. When the object comes back to the mean position, its velocity is at its maximum. Thus, in this case, the potential is converted to kinetic energy and vice versa. In an ideal simple harmonic motion, the energy is conserved. Even though it might change forms, the total energy remains constant. It is essential to study these changes in energy and the total energy to analyze the SHM and its properties. Let’s look at that in detail.
Simple Harmonic Motion
Simple Harmonic Motion is a kind of periodic motion where the object moves to and fro around its mean position. The time period, in this case, remains constant. The time period is denoted by “T” and the distance of the mean position from the extreme position is called amplitude, it is denoted by A. The general equation for the position(x) of the object at any particular time is given by,
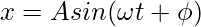
Here,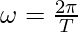 and
and 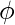 denotes the phase shift.
denotes the phase shift.
Similarly, the equation for the velocity of the object in SHM can be found by differentiating this equation.
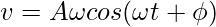
Then, the equation for acceleration becomes,
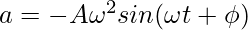
Energy in Simple Harmonic Motion
Kinetic and potential energies in the SHM vary from zero to their maximum values. The equations mentioned above show that the velocity of the object follows the sinusoidal trajectory, which means that the velocity of the object increases and decreases. The velocity is zero at the extreme positions and maximum at the mean positions. The position where the velocity is maximum is the position where the kinetic energy of the object is also maximum.
For an object of mass “m”, with a velocity “v”. Kinetic energy is given by,
KE = 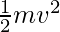
Since the object is in SHM, the value of the velocity can be substituted into the equation,
KE = 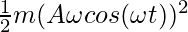
⇒ KE = 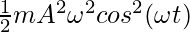
⇒ KE =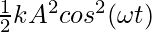
Notice that the KE is also in the form of a periodic equation.
Maximum Value of K.E =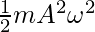 (At the mean position)
(At the mean position)
Minimum Value of K.E = 0 (At the extreme position)
In the case of conservative forces, which are directly proportional to the displacement. The potential energy is given by,
U = 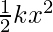
Substituting the value of x(t) in SHM,
U = 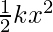
⇒ U(t) = 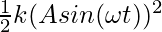
⇒ U(t) = 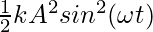
Let’s find the total energy,
E = U + K
⇒ E =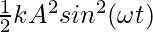 +
+ 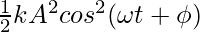
⇒ E = ![Rendered by QuickLaTeX.com \frac{1}{2}kA^2[sin^2(\omega t) + cos^2(\omega t)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-05801571af8e8b19e0adb4e3399bf0cd_l3.png)
⇒ E = 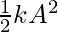

The figure above shows the graph of KE and PE and the total energy E of the SHM. In this case, notice that the total energy of the system remains constant and independent of time.
Sample Problems
Question 1: A particle of mass 10Kg is performing SHM where its position is given by the equation given below,
x(t) = 3sin(5t)
Find its kinetic energy at the mean position.
Answer:
The KE at the mean position is given by,
K.E =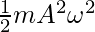
In this case, A = 3, m = 10Kg and 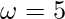
K.E =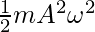
⇒ K.E = 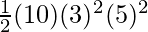
⇒ K.E = 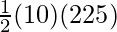
⇒ K.E = 1225 J
Question 2: A particle of mass 2Kg is performing SHM where its position is given by the equation given below,
x(t) = cos(2t)
Find its kinetic energy at the mean position.
Answer:
The KE at the mean position is given by,
K.E =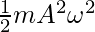
In this case, A = 1, m = 2Kg and 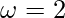
K.E =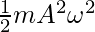
⇒ K.E = 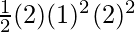
⇒ K.E = 4 J.
Question 3: A particle of mass 2Kg is performing SHM connected to a spring (k = 100 N/m) where its position is given by the equation given below,
x(t) = 20cos(t)
Find its potential energy at the extreme position.
Answer:
The KE at the mean position is given by,
U(t) = 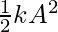
In this case, A = 20, k =100 and 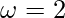
U(t) = 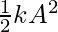
⇒ U(t) = 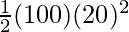
⇒ U(t) = 20000 J
Question 4: A particle of mass 1Kg is performing SHM connected to a spring (k = 10 N/m) where its position is given by the equation given below,
x(t) = 2cos(t)
Find its potential energy at the extreme position.
Answer:
The KE at the mean position is given by,
U(t) = 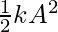
In this case, A = 2, k =10 and 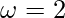
U(t) = 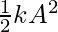
⇒ U(t) = 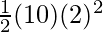
⇒ U(t) = 20 J
Question 5: A particle is performing SHM where its position is given by the equation given below,
x(t) = 2sin(10t)
Find its velocity at the mean position.
Answer:
The KE at the mean position is given by,
K.E =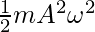
In this case, A = 2 and 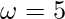
K.E =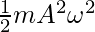
⇒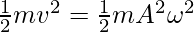
⇒ 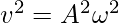
⇒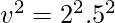
⇒ v = 10 m/s
Question 6: A particle is performing SHM where its position is given by the equation given below,
x(t) = 10cos(10t + 5)
Find its velocity at the mean position.
Answer:
The KE at the mean position is given by,
K.E =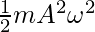
In this case, A = 10 and 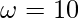
K.E =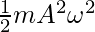
⇒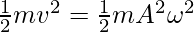
⇒ 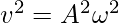
⇒v2 = 102(10)2
⇒ v = 100 m/s
Share your thoughts in the comments
Please Login to comment...