Precomputation Techniques for Competitive Programming
Last Updated :
23 Apr, 2024
What is the Pre-Computation Technique?
Precomputation refers to the process of pre-calculating and storing the results of certain computations or data structures in advance, in order to speed up the execution time of a program. This can be useful in situations where the same calculations or data structures are needed multiple times, as it avoids the need to recalculate them every time.
Time-Space Trade-Off during Pre-Computation: In order to reduce the amount of time, pre-computation relies on quickly accessing the pre-existing data. We need to store that data in some sort of data structure, hence the Auxiliary space requirement increases.
Why to Use Pre-Computation?
A variety of questions in competitive programming requires printing solution for each Query. Test cases are designed in such a way that if a programmer computes solution again and again for each query then it may result in TLE (Time Limit Exceed).
Pre-Computation allows to store a part of solution before processing the queries and then for each query instead of calculating the solution we just need to retrieve that solution.
For example, let’s say you have Q queries and each query requires to traverse an array of size N, this will result in a time complexity of O(Q*N), imagine if we can precompute and store the data in O(N) time and then process each query in O(1) time, then we can clearly see that the complexity drastically drops to O(max(Q,N)).
Use-Cases of Pre-Computation in Competitive Programming:
1. Prefix/Suffix Arrays:
Our Requirement: We have an array arr[] of size N and for T number of test cases we want to get the following information in O(1)
Pre-Computation Approach: Before processing the test cases we can precompute the required data in O(N) as follows:
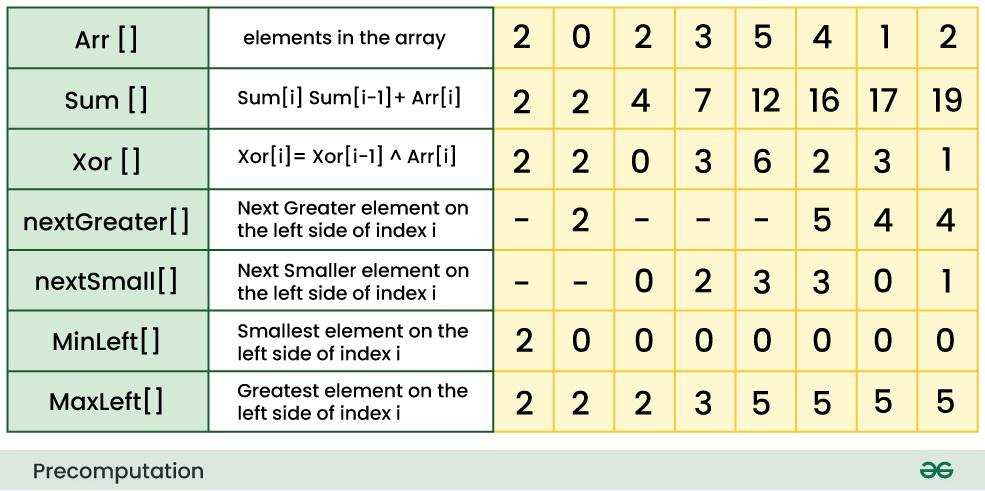
Using the above table we can calcultate our requirement in O(1) as:
- Sum of elements from index L to R = Sum[R]- Sum[L-1]
- Xor of elements from index L to R = Xor[R]- Xor[L-1]
- Next Greater element on left of i = nextGreater[i]
- Next Smaller element on left of i = nextSmall[i]
- Smallest element on left of i = MinLeft[i]
- Greatest element on left of i = MaxLeft[i]
Click here to expand your knowledge about Prefix/Suffix Arrays:
Code Snippet for Pre-Computation:
C++
int prefixSum[100000];
int prefixXor[100000];
int minLeft[100000];
int maxLeft[100000];
void preCompute(int n, vector<int> arr)
{
prefixSum[0] = prefixXor[0] = minLeft[0] = maxLeft[0]
= arr[0];
for (int i = 1; i < n; i++) {
prefixSum[i] = prefixSum[i - 1] + arr[i];
prefixXor[i] = prefixXor[i - 1] + arr[i];
minLeft[i] = min(minLeft[i - 1] + arr[i]);
maxLeft[i] = max(maxLeft[i - 1] + arr[i]);
}
}
int[] prefixSum = new int[100000];
int[] prefixXor = new int[100000];
int[] minLeft = new int[100000];
int[] maxLeft = new int[100000];
void preCompute(int n, int[] arr) {
prefixSum[0] = prefixXor[0] = minLeft[0] = maxLeft[0] = arr[0];
for (int i = 1; i < n; i++) {
prefixSum[i] = prefixSum[i - 1] + arr[i];
prefixXor[i] = prefixXor[i - 1] ^ arr[i];
minLeft[i] = Math.min(minLeft[i - 1], arr[i]);
maxLeft[i] = Math.max(maxLeft[i - 1], arr[i]);
}
}
# Initialize arrays with size 100000
prefixSum = [0] * 100000
prefixXor = [0] * 100000
minLeft = [0] * 100000
maxLeft = [0] * 100000
def preCompute(n, arr):
# Initialize values for the first element
prefixSum[0] = prefixXor[0] = minLeft[0] = maxLeft[0] = arr[0]
# Compute prefix sums, XORs, minimums, and maximums
for i in range(1, n):
prefixSum[i] = prefixSum[i - 1] + arr[i]
prefixXor[i] = prefixXor[i - 1] ^ arr[i]
minLeft[i] = min(minLeft[i - 1], arr[i])
maxLeft[i] = max(maxLeft[i - 1], arr[i])
# Example usage
n = 5
arr = [2, 3, 1, 4, 5]
preCompute(n, arr)
# Print the computed arrays
print("Prefix Sum:", prefixSum)
print("Prefix XOR:", prefixXor)
print("Min Left:", minLeft)
print("Max Left:", maxLeft)
using System;
using System.Collections.Generic;
class Program {
static int[] PrefixSum = new int[100000];
static int[] PrefixXor = new int[100000];
static int[] MinLeft = new int[100000];
static int[] MaxLeft = new int[100000];
static void PreCompute(int n, List<int> arr)
{
PrefixSum[0] = PrefixXor[0] = MinLeft[0]
= MaxLeft[0] = arr[0];
for (int i = 1; i < n; i++) {
PrefixSum[i] = PrefixSum[i - 1] + arr[i];
PrefixXor[i] = PrefixXor[i - 1] ^ arr[i];
MinLeft[i] = Math.Min(MinLeft[i - 1], arr[i]);
MaxLeft[i] = Math.Max(MaxLeft[i - 1], arr[i]);
}
}
static void Main()
{
int n = 5; // Example size
List<int> arr = new List<int>{ 2, 5, 3, 7,
1 }; // Example array
PreCompute(n, arr);
// Print the computed arrays
Console.WriteLine("PrefixSum: ["
+ string.Join(", ", PrefixSum)
+ "]");
Console.WriteLine("PrefixXor: ["
+ string.Join(", ", PrefixXor)
+ "]");
Console.WriteLine("MinLeft: ["
+ string.Join(", ", MinLeft)
+ "]");
Console.WriteLine("MaxLeft: ["
+ string.Join(", ", MaxLeft)
+ "]");
}
}
// Initialize arrays with size 100000
const prefixSum = new Array(100000).fill(0);
const prefixXor = new Array(100000).fill(0);
const minLeft = new Array(100000).fill(0);
const maxLeft = new Array(100000).fill(0);
function preCompute(n, arr) {
// Initialize values for the first element
prefixSum[0] = prefixXor[0] = minLeft[0] = maxLeft[0] = arr[0];
// Compute prefix sums, XORs, minimums, and maximums
for (let i = 1; i < n; i++) {
prefixSum[i] = prefixSum[i - 1] + arr[i];
prefixXor[i] = prefixXor[i - 1] ^ arr[i];
minLeft[i] = Math.min(minLeft[i - 1], arr[i]);
maxLeft[i] = Math.max(maxLeft[i - 1], arr[i]);
}
}
// Example usage
const n = 5;
const arr = [2, 3, 1, 4, 5];
preCompute(n, arr);
// Print the computed arrays
console.log("Prefix Sum:", prefixSum);
console.log("Prefix XOR:", prefixXor);
console.log("Min Left:", minLeft);
console.log("Max Left:", maxLeft);
2. Pre-Computing Prime Number using Sieve of Eratosthenes in O(nlog(log(n)) to check if a number is prime in O(1):
Let assume, there are Q queries and for each query we have to check if a number is Prime or not.
Brute force: For each query we can check if a number n is prime or not in 
Optimal approach: Use sieve of eratosthenes to store the Primality in O(Nlog(logN)) and for each query we can check if a number is prime or not in O(1)
Complexity Analysis:
- Brute force:
 )
) - Pre-Computation: O(max(Q, Nlog(logN)))
Code Snippet of check if a number is prime in O(1):
C++
bool prime[N];
void PreComputeSeive()
{
fill(prime, prime + N, true);
prime[0] = prime[1] = false;
for (int i = 2; i * i <= N; i++) {
if (prime[i] == true) {
for (int j = i * i; j < N; j += i) {
prime[j] = false;
}
}
}
}
public class SieveOfEratosthenes {
static final int N = 1000; // Adjust the size of the array as needed
static boolean[] prime = new boolean[N];
public static void preComputeSieve() {
// Initializing the boolean array
for (int i = 0; i < N; i++) {
prime[i] = true;
}
prime[0] = prime[1] = false;
// Sieve of Eratosthenes algorithm
for (int i = 2; i * i <= N; i++) {
if (prime[i]) {
for (int j = i * i; j < N; j += i) {
prime[j] = false;
}
}
}
}
public static void main(String[] args) {
preComputeSieve();
// Print prime numbers or use them as needed
System.out.println("Prime numbers up to " + (N - 1) + ":");
for (int i = 2; i < N; i++) {
if (prime[i]) {
System.out.print(i + " ");
}
}
}
}
N = 1000
prime = [True] * (N + 1)
def pre_compute_sieve():
global prime
prime[0] = prime[1] = False
for i in range(2, int(N**0.5) + 1):
if prime[i]:
for j in range(i * i, N + 1, i):
prime[j] = False
# Driver Code
pre_compute_sieve()
print(prime)
using System;
public class SieveOfEratosthenes
{
const int N = 1000; // Adjust the size of the array as needed
static bool[] prime = new bool[N];
public static void PreComputeSieve()
{
// Initializing the boolean array
for (int i = 0; i < N; i++)
{
prime[i] = true;
}
prime[0] = prime[1] = false;
// Sieve of Eratosthenes algorithm
for (int i = 2; i * i <= N; i++)
{
if (prime[i])
{
for (int j = i * i; j < N; j += i)
{
prime[j] = false;
}
}
}
}
public static void Main(string[] args)
{
PreComputeSieve();
// Print prime numbers or use them as needed
Console.WriteLine($"Prime numbers up to {N - 1}:");
for (int i = 2; i < N; i++)
{
if (prime[i])
{
Console.Write(i + " ");
}
}
}
}
// Define the value of N
let N = 1000;
// Initialize an array to track whether each number up to N is prime
let prime = Array(N + 1).fill(true);
// Function to pre-compute prime numbers up to N using the Sieve of Eratosthenes algorithm
function preComputeSieve() {
// Mark 0 and 1 as non-prime
prime[0] = prime[1] = false;
// Loop through numbers from 2 up to the square root of N
for (let i = 2; i <= Math.sqrt(N); i++) {
// If i is prime
if (prime[i]) {
// Mark all multiples of i as non-prime
for (let j = i * i; j <= N; j += i) {
prime[j] = false;
}
}
}
}
// Call the pre-computation function
preComputeSieve();
// Output the prime array, indicating whether each number up to N is prime
console.log(prime);
//This code is contributed by Adarsh
3. Pre-Computing Prime Number using Sieve of Eratosthenes in O(nlog(log(n)) to get smallest prime factor of a number in O(1):
Lets assume, there are ‘Q’ queries and for each query we want to get smallest prime factor of a number ‘n’.
Brute force: For each query we can get first prime factor of n in 
Optimal approach: Use sieve of eratosthenes to store the Primality in O(Nlog(logN)) and for each query we can check if a number is prime or not in O(1)
Complexity Analysis:
- Brute force:

- Pre-Computation:

Code Snippet to get smallest prime factor of a number in O(1):
C++
#include <iostream>
#include <vector>
using namespace std;
const int N = 1000000; // Assuming a maximum value for N
// Arrays to store smallest prime factor (spf) and prime flags
int spf[N];
bool prime[N];
// Function to perform Sieve of Eratosthenes algorithm
void sieve() {
// Initialize the spf array with indices
for (int i = 0; i < N; i++) {
spf[i] = i;
}
// Initialize the prime array and mark 0 and 1 as not prime
fill(prime, prime + N, true);
prime[0] = prime[1] = false;
// Iterate over numbers starting from 2 and mark multiples as not prime
for (int i = 2; i * i <= N; i++) {
if (prime[i]) {
// Mark multiples of i as not prime
for (int j = i * i; j < N; j += i) {
prime[j] = false;
// Update smallest prime factor (spf) if not updated before
if (spf[j] == j) {
spf[j] = i;
}
}
}
}
}
// Utility method to fill an array with a given value
template <typename T>
void fill(T arr[], T value, int size) {
for (int i = 0; i < size; i++) {
arr[i] = value;
}
}
// Main method (for testing)
int main() {
// Call the sieve method to generate primes and smallest prime factors
sieve();
// Print some results (you can customize this part)
cout << "Prime numbers up to 100:" << endl;
for (int i = 0; i <= 100; i++) {
if (prime[i]) {
cout << i << " ";
}
}
cout << endl;
cout << "Smallest prime factors up to 20:" << endl;
for (int i = 1; i <= 20; i++) {
cout << "smallest prime factor of " << i << " is: " << spf[i] << endl;
}
return 0;
}
public class SieveOfEratosthenes {
static final int N = 1000000; // Assuming a maximum value for N
// Arrays to store smallest prime factor (spf) and prime flags
static int[] spf = new int[N];
static boolean[] prime = new boolean[N];
// Function to perform Sieve of Eratosthenes algorithm
static void sieve() {
// Initialize the spf array with indices
for (int i = 0; i < N; i++) {
spf[i] = i;
}
// Initialize the prime array and mark 0 and 1 as not prime
fill(prime, true);
prime[0] = prime[1] = false;
// Iterate over numbers starting from 2 and mark multiples as not prime
for (int i = 2; i * i <= N; i++) {
if (prime[i]) {
// Mark multiples of i as not prime
for (int j = i * i; j < N; j += i) {
prime[j] = false;
// Update smallest prime factor (spf) if not updated before
if (spf[j] == j) {
spf[j] = i;
}
}
}
}
}
// Utility method to fill a boolean array with a given value
static void fill(boolean[] arr, boolean value) {
for (int i = 0; i < arr.length; i++) {
arr[i] = value;
}
}
// Main method (for testing)
public static void main(String[] args) {
// Call the sieve method to generate primes and smallest prime factors
sieve();
// Print some results (you can customize this part)
System.out.println("Prime numbers up to 100:");
for (int i = 0; i <= 100; i++) {
if (prime[i]) {
System.out.print(i + " ");
}
}
System.out.println("\nSmallest prime factors up to 20:");
for (int i = 1; i <= 20; i++) {
System.out.println("smallest prime factor of " + i + " is: " + spf[i]);
}
}
}
import math
N = 1000000 # Assuming a maximum value for N
# Lists to store smallest prime factor (spf) and prime flags
spf = [i for i in range(N)]
prime = [True] * N
# Function to perform Sieve of Eratosthenes algorithm
def sieve():
global spf, prime
# Initialize the spf list with indices
for i in range(N):
spf[i] = i
# Initialize the prime list and mark 0 and 1 as not prime
prime[0] = prime[1] = False
# Iterate over numbers starting from 2 and mark multiples as not prime
for i in range(2, int(math.sqrt(N)) + 1):
if prime[i]:
# Mark multiples of i as not prime
for j in range(i * i, N, i):
prime[j] = False
# Update smallest prime factor (spf) if not updated before
if spf[j] == j:
spf[j] = i
# Main method (for testing)
def main():
global spf, prime
# Call the sieve method to generate primes and smallest prime factors
sieve()
# Print some results (you can customize this part)
print("Prime numbers up to 100:")
for i in range(101):
if prime[i]:
print(i, end=" ")
print()
print("Smallest prime factors up to 20:")
for i in range(1, 21):
print("Smallest prime factor of", i, "is:", spf[i])
if __name__ == "__main__":
main()
using System;
public class Program {
const int N = 200001;
static int[] spf = new int[N];
static bool[] prime = new bool[N];
// Method to find all prime numbers up to N using the
// Sieve of Eratosthenes algorithm
static void Sieve()
{
// Initialize spf array with initial values
for (int i = 0; i < N; i++) {
spf[i] = i;
}
// Assume all numbers are prime initially
Array.Fill(prime, true);
prime[0] = prime[1] = false;
// Iterate over numbers up to the square root of N
for (int i = 2; i * i < N; i++) {
// If i is prime
if (prime[i]) {
// Mark multiples of i as non-prime
for (int j = i * i; j < N; j += i) {
prime[j] = false;
// If spf[j] is still j, it means j is
// not yet assigned any prime factor
if (spf[j] == j) {
// Assign i as the smallest prime
// factor of j
spf[j] = i;
}
}
}
}
}
// Main method, entry point of the program
public static void Main(string[] args)
{
// Call the Sieve method to generate prime numbers
Sieve();
// Output for demonstration (optional)
for (int i = 0; i < N; i++) {
if (prime[i]) {
Console.WriteLine($
"{i} is a prime number.");
}
}
}
}
const N = 1000000; // Assuming a maximum value for N
// Arrays to store smallest prime factor (spf) and prime flags
const spf = new Array(N).fill(0);
const prime = new Array(N).fill(true);
// Function to perform Sieve of Eratosthenes algorithm
function sieve() {
// Initialize the spf array with indices
for (let i = 0; i < N; i++) {
spf[i] = i;
}
// Initialize the prime array and mark 0 and 1 as not prime
fill(prime, true);
prime[0] = prime[1] = false;
// Iterate over numbers starting from 2 and mark multiples as not prime
for (let i = 2; i * i <= N; i++) {
if (prime[i]) {
// Mark multiples of i as not prime
for (let j = i * i; j < N; j += i) {
prime[j] = false;
// Update smallest prime factor (spf) if not updated before
if (spf[j] === j) {
spf[j] = i;
}
}
}
}
}
// Utility method to fill an array with a given value
function fill(arr, value) {
for (let i = 0; i < arr.length; i++) {
arr[i] = value;
}
}
// Main method (for testing)
function main() {
// Call the sieve method to generate primes and smallest prime factors
sieve();
// Print some results (you can customize this part)
console.log("Prime numbers up to 100:");
for (let i = 0; i <= 100; i++) {
if (prime[i]) {
process.stdout.write(i + " ");
}
}
console.log("\nSmallest prime factors up to 20:");
for (let i = 1; i <= 20; i++) {
console.log("smallest prime factor of " + i + " is: " + spf[i]);
}
}
// Call the main method to execute the code
main();
4. Pre-Computing Factorial and Inverse Factorial in O(N) to compute nCr in O(1):
Lets assume, We have T number of test cases and for each test case we want to get FATORIAL , INVERSE FACTORIAL for a number ‘n‘ , also we want calculate to calculate nCr in O(1)
Brute Force: For each test case we can calculate the above requirements in O(N) for a number N.
Optimal approach:
- We can pre-compute the factorial of all the numbers for 1 to N in O(N) using the following recurence:
- factorial[i] = i * factorial[i-1]
- Also inverse factorial can be calculated as:
- invfact[i]= (i+1) * invfact[i+1];
- nCr can be calculated as:
- factorial[n] * inverseFactorial[r] * inverseFactorial[n-r]
Complexity Analysis:
- Brute Force: O(T * N)
- Precomputaion approach: O(max(T, N))
Code Snippet to to compute nCr in O(1):
C++
#include <iostream>
using namespace std;
const int N = 1000001;
const int mod = 1000000007;
int fact[N], invfact[N];
int mul(int a, int b) {
return (1LL * a * b) % mod;
}
int power(int x, int y) {
int res = 1;
x = x % mod;
while (y > 0) {
if (y & 1) {
res = mul(res, x);
}
y >>= 1;
x = mul(x, x);
}
return res;
}
void initNCR() {
fact[0] = 1;
int i;
for (i = 1; i < N; i++) {
fact[i] = mul(i, fact[i - 1]);
}
i--;
invfact[i] = power(fact[i], mod - 2);
for (i--; i >= 0; i--) {
invfact[i] = mul((i + 1), invfact[i + 1]);
}
}
int ncr(int n, int r) {
if (r > n || n < 0 || r < 0)
return 0;
return mul(mul(fact[n], invfact[r]), invfact[n - r]);
}
int main() {
// Initialize the precomputed factorials and inverse factorials
initNCR();
// Example usage:
int n = 5;
int r = 2;
cout << "ncr(" << n << "," << r << ") = " << ncr(n, r) << endl;
return 0;
}
public class Main {
static final int N = 1000001;
static final int mod = 1000000007;
static int[] fact = new int[N];
static int[] invfact = new int[N];
static int mul(int a, int b) {
return (int) (((long) a * b) % mod);
}
static int power(int x, int y) {
int res = 1;
x = x % mod;
while (y > 0) {
if ((y & 1) == 1) {
res = mul(res, x);
}
y >>= 1;
x = mul(x, x);
}
return res;
}
static void initNCR() {
fact[0] = 1;
for (int i = 1; i < N; i++) {
fact[i] = mul(i, fact[i - 1]);
}
int i = N - 1;
invfact[i] = power(fact[i], mod - 2);
i--;
while (i >= 0) {
invfact[i] = mul((i + 1), invfact[i + 1]);
i--;
}
}
static int ncr(int n, int r) {
if (r > n || n < 0 || r < 0) {
return 0;
}
return mul(mul(fact[n], invfact[r]), invfact[n - r]);
}
public static void main(String[] args) {
// Initialize the precomputed factorials and inverse factorials
initNCR();
// Example usage:
int n = 5;
int r = 2;
System.out.println("ncr(" + n + "," + r + ") = " + ncr(n, r));
}
}
N = 1000001
mod = 1000000007
fact = [0] * N
invfact = [0] * N
def mul(a, b):
return (a * b) % mod
def power(x, y):
res = 1
x = x % mod
while y > 0:
if y & 1:
res = (res * x) % mod
y = y >> 1
x = (x * x) % mod
return res
def initNCR():
fact[0] = 1
for i in range(1, N):
fact[i] = mul(i, fact[i - 1])
i = N - 1
invfact[i] = power(fact[i], mod - 2)
i -= 1
while i >= 0:
invfact[i] = mul((i + 1), invfact[i + 1])
i -= 1
def ncr(n, r):
if r > n or n < 0 or r < 0:
return 0
return mul(mul(fact[n], invfact[r]), invfact[n - r])
# Initialize the precomputed factorials and inverse factorials
initNCR()
# Example usage:
n = 5
r = 2
print("ncr(", n, ",", r, ") =", ncr(n, r))
#this code is contributed b y Adarsh
const N = 1000001;
const mod = 1000000007;
// Function to compute the modular exponentiation (a^b) % mod
function power(a, b) {
let result = 1;
a = a % mod;
while (b > 0) {
if (b % 2 === 1)
result = (result * a) % mod;
b = Math.floor(b / 2);
a = (a * a) % mod;
}
return result;
}
// Function to compute the modular multiplication (a * b) % mod
function mul(a, b) {
return ((a % mod) * (b % mod)) % mod;
}
// Function to initialize the factorial and inverse factorial arrays
function initNCR() {
const fact = new Array(N);
const invfact = new Array(N);
fact[0] = 1;
for (let i = 1; i < N; i++) {
fact[i] = mul(i, fact[i - 1]);
}
let i = N - 1;
invfact[i] = power(fact[i], mod - 2);
for (i--; i >= 0; i--) {
invfact[i] = mul((i + 1), invfact[i + 1]);
}
// Return the initialized arrays
return { fact, invfact };
}
// Function to compute nCr using precomputed factorials and inverse factorials
function ncr(n, r, fact, invfact) {
if (r > n || n < 0 || r < 0)
return 0;
return mul(mul(fact[n], invfact[r]), invfact[n - r]);
}
// Initialize the factorial and inverse factorial arrays
const { fact, invfact } = initNCR();
// Example usage:
const n = 5;
const r = 2;
console.log(ncr(n, r, fact, invfact)); // Output: 10
5. Pre-Computation On Strings:
Lets assume, We have a string S and Q queries, for each query we want to get the number of occurance of a character in index range L to R.
Brute Force: For each query we can iterate the string from index L to R to know the occurance of desired character in O(N)
Pre-computation approach: We can precompute a 2-D prefix array pSum[][] such that pSum[i][j] stores the number of occurences of j’th aphabet till index i. To compute our require we can use the following formula:
- Occurrence of j’th character between index L to R = pSum[R][j] – pSum[L-1][j]
Code Snippet of Pre-Computation On Strings:
C++
#include <bits/stdc++.h>
using namespace std;
vector<int> preComputation(string s,
vector<vector<int>>& queries,
vector<char>& character)
{
int n = s.size();
// Create a 2D vector to store prefix sum of
// character occurrences
vector<vector<int>> psum(n + 1, vector<int>(26, 0));
// Calculate prefix sums
for (int i = 1; i <= n; i++) {
for (int j = 0; j < 26; j++) {
// Update prefix sum
psum[i][j] = psum[i - 1][j];
}
// Increment the count of current character
psum[i][s[i - 1] - 'a']++;
}
int m = queries.size();
vector<int> ans(m);
// Calculate answers for each query
for (int i = 0; i < m; i++) {
// Calculate the count of character within the
// specified range
ans[i] = psum[queries[i][1]][character[i] - 'a'] - psum[queries[i][0] - 1][character[i] - 'a'];
}
return ans;
}
import java.util.*;
public class Main {
// Function to perform precomputation and answer queries
public static List<Integer> preComputation(String s, List<List<Integer>> queries, List<Character> characters) {
int n = s.length();
// Create a 2D array to store prefix sum of character occurrences
int[][] psum = new int[n + 1][26];
// Calculate prefix sums
for (int i = 1; i <= n; i++) {
for (int j = 0; j < 26; j++) {
// Update prefix sum
psum[i][j] += psum[i - 1][j];
}
// Increment the count of current character
psum[i][s.charAt(i - 1) - 'a']++;
}
int m = queries.size();
List<Integer> ans = new ArrayList<>();
// Calculate answers for each query
for (int i = 0; i < m; i++) {
// Calculate the count of character within the specified range
ans.add(psum[queries.get(i).get(1)][characters.get(i) - 'a']
- psum[queries.get(i).get(0) - 1][characters.get(i) - 'a']);
}
return ans;
}
}
//This code is contributed by MoNu.
6. Pre-Computation on Trees:
Pre-Computation on trees mainly rely on a node storing information about its subtree, this allows the tree traversal to skip certain nodes and hence reduces the complexity to the height of he tree in most of the cases.
Below data can be pre-computed in case of a tree:
Real World Application of Pre-Computation:
- Precomputation in Databases
- Precomputation in Data Analytics
- Machine Learning and AI
- Pathfinding
- Recommendation Systems
Key Takeaways:
- Precomputation is a common technique that uses fast information retrieval rather than computing again and again.
- It’s a trade-off between time and space.
- Different question requires different pre-computation techniques hence to tackle those problem the best we can do is to practice a lot of problems.
Practice problems on Precomputation Techniques:
Share your thoughts in the comments
Please Login to comment...