Range sum query using Sparse Table
Last Updated :
21 Aug, 2022
We have an array arr[]. We need to find the sum of all the elements in the range L and R where 0 <= L <= R <= n-1. Consider a situation when there are many range queries.
Examples:
Input : 3 7 2 5 8 9
query(0, 5)
query(3, 5)
query(2, 4)
Output : 34
22
15
Note : array is 0 based indexed
and queries too.
Since there are no updates/modifications, we use the Sparse table to answer queries efficiently. In a sparse table, we break queries in powers of 2.
Suppose we are asked to compute sum of
elements from arr[i] to arr[i+12].
We do the following:
// Use sum of 8 (or 23) elements
table[i][3] = sum(arr[i], arr[i + 1], ...
arr[i + 7]).
// Use sum of 4 elements
table[i+8][2] = sum(arr[i+8], arr[i+9], ..
arr[i+11]).
// Use sum of single element
table[i + 12][0] = sum(arr[i + 12]).
Our result is sum of above values.
Notice that it took only 4 actions to compute the result over a subarray of size 13.
Flowchart:
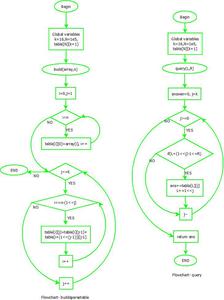
Flowchart
C++
#include <bits/stdc++.h>
using namespace std;
const int k = 16;
const int N = 1e5;
long long table[N][k + 1];
void buildSparseTable(int arr[], int n)
{
for (int i = 0; i < n; i++)
table[i][0] = arr[i];
for (int j = 1; j <= k; j++)
for (int i = 0; i <= n - (1 << j); i++)
table[i][j] = table[i][j - 1] +
table[i + (1 << (j - 1))][j - 1];
}
long long query(int L, int R)
{
long long answer = 0;
for (int j = k; j >= 0; j--) {
if (L + (1 << j) - 1 <= R) {
answer = answer + table[L][j];
L += 1 << j;
}
}
return answer;
}
int main()
{
int arr[] = { 3, 7, 2, 5, 8, 9 };
int n = sizeof(arr) / sizeof(arr[0]);
buildSparseTable(arr, n);
cout << query(0, 5) << endl;
cout << query(3, 5) << endl;
cout << query(2, 4) << endl;
return 0;
}
|
Java
class GFG
{
static int k = 16;
static int N = 100000;
static long table[][] = new long[N][k + 1];
static void buildSparseTable(int arr[],
int n)
{
for (int i = 0; i < n; i++)
table[i][0] = arr[i];
for (int j = 1; j <= k; j++)
for (int i = 0; i <= n - (1 << j); i++)
table[i][j] = table[i][j - 1] +
table[i + (1 << (j - 1))][j - 1];
}
static long query(int L, int R)
{
long answer = 0;
for (int j = k; j >= 0; j--)
{
if (L + (1 << j) - 1 <= R)
{
answer = answer + table[L][j];
L += 1 << j;
}
}
return answer;
}
public static void main(String args[])
{
int arr[] = { 3, 7, 2, 5, 8, 9 };
int n = arr.length;
buildSparseTable(arr, n);
System.out.println(query(0, 5));
System.out.println(query(3, 5));
System.out.println(query(2, 4));
}
}
|
C#
using System;
class GFG
{
static int k = 16;
static int N = 100000;
static long [,]table =
new long[N, k + 1];
static void buildSparseTable(int []arr,
int n)
{
for (int i = 0; i < n; i++)
table[i, 0] = arr[i];
for (int j = 1; j <= k; j++)
for (int i = 0;
i <= n - (1 << j); i++)
table[i, j] = table[i, j - 1] +
table[i + (1 << (j - 1)), j - 1];
}
static long query(int L, int R)
{
long answer = 0;
for (int j = k; j >= 0; j--)
{
if (L + (1 << j) - 1 <= R)
{
answer = answer +
table[L, j];
L += 1 << j;
}
}
return answer;
}
static void Main()
{
int []arr = new int[]{3, 7, 2,
5, 8, 9};
int n = arr.Length;
buildSparseTable(arr, n);
Console.WriteLine(query(0, 5));
Console.WriteLine(query(3, 5));
Console.WriteLine(query(2, 4));
}
}
|
Python3
k = 16
n = 100000
table = [[0 for j in range(k+1)] for i in range(n)]
def buildSparseTable(arr, n):
global table, k
for i in range(n):
table[i][0] = arr[i]
for j in range(1,k+1):
for i in range(0,n-(1<<j)+1):
table[i][j] = table[i][j-1] + \
table[i + (1 << (j - 1))][j - 1]
def query(L, R):
global table, k
answer = 0
for j in range(k,-1,-1):
if (L + (1 << j) - 1 <= R):
answer = answer + table[L][j]
L+=1<<j
return answer
if __name__ == '__main__':
arr = [3, 7, 2, 5, 8, 9]
n = len(arr)
buildSparseTable(arr, n)
print(query(0,5))
print(query(3,5))
print(query(2,4))
|
Javascript
<script>
const k = 16;
const N = 1e5;
const table = new Array(N).fill(0).map(() => new Array(k + 1).fill(0));
function buildSparseTable(arr, n)
{
for (let i = 0; i < n; i++)
table[i][0] = arr[i];
for (let j = 1; j <= k; j++)
for (let i = 0; i <= n - (1 << j); i++)
table[i][j] = table[i][j - 1] +
table[i + (1 << (j - 1))][j - 1];
}
function query(L, R)
{
let answer = 0;
for (let j = k; j >= 0; j--)
{
if (L + (1 << j) - 1 <= R)
{
answer = answer + table[L][j];
L += 1 << j;
}
}
return answer;
}
let arr = [ 3, 7, 2, 5, 8, 9 ];
let n = arr.length;
buildSparseTable(arr, n);
document.write(query(0, 5) + "<br>");
document.write(query(3, 5) + "<br>");
document.write(query(2, 4) + "<br>");
</script>
|
Output:
34
22
15
This algorithm for answering queries with Sparse Table works in O(k), which is O(log(n)) because we choose minimal k such that 2^k+1 > n.
Time complexity of sparse table construction : Outer loop runs in O(k), inner loop runs in O(n). Thus, in total we get O(n * k) = O(n * log(n))
Auxiliary Space: O(n*k), since n*k extra space has been taken.
Share your thoughts in the comments
Please Login to comment...