Painting Fence Algorithm
Last Updated :
12 Apr, 2024
Given a fence with n posts and k colors, find out the number of ways of painting the fence such that at most 2 adjacent posts have the same color. Since the answer can be large, return it modulo 10^9 + 7.
Examples:
Input : n = 2 k = 4
Output : 16
Explanation: We have 4 colors and 2 posts.
Ways when both posts have same color : 4
Ways when both posts have diff color :4(choices for 1st post) * 3(choices for 2nd post) = 12
Input : n = 3 k = 2
Output : 6
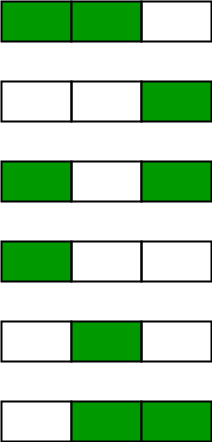
The following image depicts the 6 possible ways of painting 3 posts with 2 colors:
Consider the following image, in which c, c’ and c” are the respective colors of posts i, i-1, and i -2.
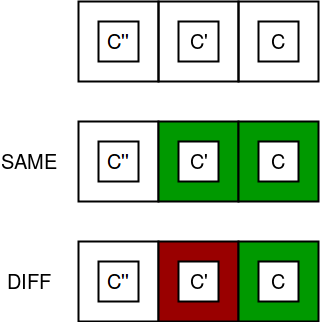
According to the constraint of the problem, c = c’ = c” is not possible simultaneously, so either c’ != c or c” != c or both. There are k – 1 possibility for c’ != c and k – 1 for c” != c.
diff = number of ways when color of last
two posts is different
same = number of ways when color of last
two posts is same
Total ways = diff + same
for n = 1
diff = k, same = 0
total = k
for n = 2
diff = k * (k-1) //k choices for
first post, k-1 for next
same = k/k choices for common
color of two posts
total = k + k * (k-1)
for n = 3
diff = (previous total ways) * (k - 1)
(k + k * (k - 1) * (k - 1)
same = previous diff ways
k * (k-1)
Hence, we deduce that,
total[i] = same[i] + diff[i]
same[i] = diff[i-1]
diff[i] = total[i-1] * (k-1)
Below is the implementation of the problem:
C++
// C++ program for Painting Fence Algorithm
// optimised version
#include <bits/stdc++.h>
using namespace std;
// Returns count of ways to color k posts
long countWays(int n, int k)
{
long dp[n + 1];
memset(dp, 0, sizeof(dp));
long long mod = 1000000007;
dp[1] = k;
dp[2] = k * k;
for (int i = 3; i <= n; i++) {
dp[i] = ((k - 1) * (dp[i - 1] + dp[i - 2])) % mod;
}
return dp[n];
}
// Driver code
int main()
{
int n = 3, k = 2;
cout << countWays(n, k) << endl;
return 0;
}
// Java program for Painting Fence Algorithm
import java.util.*;
class GfG {
// Returns count of ways to color k posts
// using k colors
static long countWays(int n, int k)
{
// To store results for subproblems
long dp[] = new long[n + 1];
Arrays.fill(dp, 0);
int mod = 1000000007;
// There are k ways to color first post
dp[1] = k;
// There are 0 ways for single post to
// violate (same color_ and k ways to
// not violate (different color)
int same = 0, diff = k;
// Fill for 2 posts onwards
for (int i = 2; i <= n; i++) {
// Current same is same as previous diff
same = diff;
// We always have k-1 choices for next post
diff = (int)(dp[i - 1] * (k - 1));
diff = diff % mod;
// Total choices till i.
dp[i] = (same + diff) % mod;
}
return dp[n];
}
// Driver code
public static void main(String[] args)
{
int n = 3, k = 2;
System.out.println(countWays(n, k));
}
}
// This code contributed by Rajput-Ji
# Python3 program for Painting Fence Algorithm
# optimised version
# Returns count of ways to color k posts
def countWays(n, k):
dp = [0] * (n + 1)
total = k
mod = 1000000007
dp[1] = k
dp[2] = k * k
for i in range(3,n+1):
dp[i] = ((k - 1) * (dp[i - 1] + dp[i - 2])) % mod
return dp[n]
# Driver code
n = 3
k = 2
print(countWays(n, k))
# This code is contributed by shubhamsingh10
// C# program for Painting Fence Algorithm
using System;
public class GFG
{
// Returns count of ways to color k posts
// using k colors
static long countWays(int n, int k)
{
// To store results for subproblems
long[] dp = new long[n + 1];
Array.Fill(dp, 0);
int mod = 1000000007;
// There are k ways to color first post
dp[1] = k;
// There are 0 ways for single post to
// violate (same color_ and k ways to
// not violate (different color)
int same = 0, diff = k;
// Fill for 2 posts onwards
for (int i = 2; i <= n; i++)
{
// Current same is same as previous diff
same = diff;
// We always have k-1 choices for next post
diff = (int)(dp[i - 1] * (k - 1));
diff = diff % mod;
// Total choices till i.
dp[i] = (same + diff) % mod;
}
return dp[n];
}
// Driver code
static public void Main ()
{
int n = 3, k = 2;
Console.WriteLine(countWays(n, k));
}
}
// This code is contributed by avanitrachhadiya2155
<script>
// Javascript program for Painting Fence Algorithm
// Returns count of ways to color k posts
// using k colors
function countWays(n, k)
{
// To store results for subproblems
let dp = new Array(n + 1);
dp.fill(0);
let mod = 1000000007;
// There are k ways to color first post
dp[1] = k;
// There are 0 ways for single post to
// violate (same color_ and k ways to
// not violate (different color)
let same = 0, diff = k;
// Fill for 2 posts onwards
for (let i = 2; i <= n; i++)
{
// Current same is same as previous diff
same = diff;
// We always have k-1 choices for next post
diff = (dp[i - 1] * (k - 1));
diff = diff % mod;
// Total choices till i.
dp[i] = (same + diff) % mod;
}
return dp[n];
}
let n = 3, k = 2;
document.write(countWays(n, k));
// This code is contributed by divyeshrabadiya07.
</script>
Time Complexity: O(N)
Auxiliary Space: O (N)
Space optimization :
We can optimize the above solution by use one variable instead of a table.
Below is the implementation of the problem:
C++
// C++ program for Painting Fence Algorithm
#include <bits/stdc++.h>
using namespace std;
// Returns count of ways to color k posts
// using k colors
long countWays(int n, int k)
{
// There are k ways to color first post
long total = k;
int mod = 1000000007;
// There are 0 ways for single post to
// violate (same color) and k ways to
// not violate (different color)
int same = 0, diff = k;
// Fill for 2 posts onwards
for (int i = 2; i <= n; i++) {
// Current same is same as previous diff
same = diff;
// We always have k-1 choices for next post
diff = (total * (k - 1)) % mod;
// Total choices till i.
total = (same + diff) % mod;
}
return total;
}
// Driver code
int main()
{
int n = 3, k = 2;
cout << countWays(n, k) << endl;
return 0;
}
// Java program for Painting Fence Algorithm
class GFG {
// Returns count of ways to color k posts
// using k colors
static long countWays(int n, int k)
{
// There are k ways to color first post
long total = k;
int mod = 1000000007;
// There are 0 ways for single post to
// violate (same color_ and k ways to
// not violate (different color)
int same = 0, diff = k;
// Fill for 2 posts onwards
for (int i = 2; i <= n; i++) {
// Current same is same as previous diff
same = diff;
// We always have k-1 choices for next post
diff = ((int)total * (k - 1) )% mod;
// Total choices till i.
total = (same + diff) % mod;
}
return total;
}
// Driver code
public static void main(String[] args)
{
int n = 3, k = 2;
System.out.println(countWays(n, k));
}
}
// This code is contributed by Mukul Singh
# Python3 program for Painting
# Fence Algorithm
# Returns count of ways to color
# k posts using k colors
def countWays(n, k) :
# There are k ways to color first post
total = k
mod = 1000000007
# There are 0 ways for single post to
# violate (same color_ and k ways to
# not violate (different color)
same, diff = 0, k
# Fill for 2 posts onwards
for i in range(2, n + 1) :
# Current same is same as
# previous diff
same = diff
# We always have k-1 choices
# for next post
diff = (total * (k - 1)) % mod
# Total choices till i.
total = (same + diff) % mod
return total
# Driver code
if __name__ == "__main__" :
n, k = 3, 2
print(countWays(n, k))
# This code is contributed by Ryuga
// C# program for Painting Fence Algorithm
using System;
class GFG {
// Returns count of ways to color k posts
// using k colors
static long countWays(int n, int k)
{
// There are k ways to color first post
long total = k;
int mod = 1000000007;
// There are 0 ways for single post to
// violate (same color_ and k ways to
// not violate (different color)
long same = 0, diff = k;
// Fill for 2 posts onwards
for (int i = 2; i <= n; i++) {
// Current same is same as previous diff
same = diff;
// We always have k-1 choices for next post
diff = (total * (k - 1))%mod;
// Total choices till i.
total = (same + diff) % mod;
}
return total;
}
// Driver code
static void Main()
{
int n = 3, k = 2;
Console.Write(countWays(n, k));
}
}
// This code is contributed by DrRoot_
<script>
// JavaScript program for Painting Fence Algorithm
// Returns count of ways to color k posts
// using k colors
function countWays(n, k)
{
// There are k ways to color first post
let total = k;
let mod = 1000000007;
// There are 0 ways for single post to
// violate (same color_ and k ways to
// not violate (different color)
let same = 0, diff = k;
// Fill for 2 posts onwards
for (let i = 2; i <= n; i++) {
// Current same is same as previous diff
same = diff;
// We always have k-1 choices for next post
diff = (total * (k - 1))%mod;
// Total choices till i.
total = (same + diff) % mod;
}
return total;
}
let n = 3, k = 2;
document.write(countWays(n, k));
</script>
<?php
// PHP program for Painting Fence Algorithm
// Returns count of ways to color k
// posts using k colors
function countWays($n, $k)
{
// There are k ways to color first post
$total = $k;
$mod = 1000000007;
// There are 0 ways for single post to
// violate (same color_ and k ways to
// not violate (different color)
$same = 0;
$diff = $k;
// Fill for 2 posts onwards
for ($i = 2; $i <= $n; $i++)
{
// Current same is same as previous diff
$same = $diff;
// We always have k-1 choices for next post
$diff = ($total * ($k - 1)) % $mod;
// Total choices till i.
$total = ($same + $diff) % $mod;
}
return $total;
}
// Driver code
$n = 3;
$k = 2;
echo countWays($n, $k) . "\n";
// This code is contributed by ita_c
?>
Time Complexity: O(N)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...