NPDA for accepting the language L = {an bn cm | m,n>=1}
Last Updated :
28 Aug, 2019
Prerequisite –
Pushdown automata,
Pushdown automata acceptance by final state
Problem – Design a non deterministic PDA for accepting the language L = {
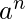
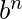
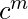
| m, n>=1}, i.e.,
L = { abc, abcc, abccc, aabbc, aaabbbcc, aaaabbbbccccc, ...... }
In each of the string, the number of a’s is equal to number of b’s. And the number of c’s is independent of the number of a’s and b’s. This problem is quite similar to the NPDA for accepting the language L = {
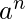
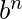
| n>=1 }. The only difference is that here we add
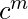
.
Explanation –
Here, we need to maintain the order of a’s, b’s and c’s.That is, all the a’s are coming first and then all the b’s and then c’s are coming. Thus, we need a stack along with the state diagram. The count of a’s and b’s is maintained by the stack. We will take 2 stack alphabets:
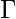 = { a, z }
= { a, z }
Where,
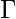
= set of all the stack alphabet
z = stack start symbol
Approach used in the construction of PDA –
As we want to design a NPDA, thus every time ‘a’ comes before ‘b’. When ‘a’ comes then push it in stack and if again ‘a’ comes then also push it. After that, when ‘b’ comes then pop one ‘a’ from the stack each time . Then for ‘c’, we will do nothing.
So, at the end if the stack becomes empty then we can say that the string is accepted by the PDA.
Stack transition functions –
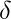 (q0, a, z)
(q0, a, z) 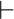 (q0, az)
(q0, az)
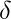 (q0, a, a)
(q0, a, a) 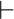 (q0, aa)
(q0, aa)
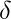 (q0, b, a)
(q0, b, a) 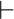 (q1,
(q1, 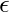 )
)
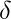 (q1, b, a)
(q1, b, a) 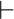 (q1,
(q1, 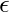 )
)
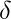 (q1, c, z)
(q1, c, z) 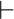 (qf, z )
(qf, z )
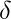 (qf, c, z)
(qf, c, z) 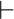 (qf, z )
(qf, z )
Where, q0 = Initial state
qf = Final state
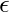
= indicates pop operation

So, this is our required non deterministic PDA for accepting the language L = {
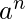
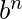
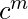
| m, n>=1 }
Share your thoughts in the comments
Please Login to comment...