Construct a Turing machine for L = {aibjck | i < j < k or i > j > k}
Last Updated :
26 Aug, 2021
Prerequisite – Turing Machine
The language L = {aibjck | i < j < k or i > j > k} is same as the union of two languages L1={aibjck | i < j < k } and L2={aibjck | i > j > k }
In this language, every string of ‘a’, ‘b’ and ‘c’ have certain number of a’s, then certain number of b’s and then certain number of c’s.
Input: a a a b b c
Here a = 3, b = 2, c = 1
Output: ACCEPTED
Input: a b b c c c
Here a = 1, b = 2, c = 3
Output: ACCEPTED
Input: a a b b c c c
Here a = 2, b = 2, c = 3 but |a|>|b|>|c| or |a|<|b|<|c|
Output: NOT ACCEPTED
Tape Representation:

Approach:
- Comparing two elements by making two element as a single element.
- After that the elements which are treated as single element are compared again .
- If |First| is greater than |(Second, Third)| and |Second| greater than |Third|, then it is accepted.
- If |Third| is greater than |(First, Second)| and |First| greater than |Second|, then it is accepted.
- Else it is not accepted.
Steps:
- Step-1: Convert A into X and move right and goto step 2.If Y is found ignore it and move right to step-5.
- Step-2: Keep ignoring A and Y and move towards right. Convert D into Y and move right and goto step-3.
- Step-3: Keep ignoring D and Z and move towards right.If C is found make it Z and move left to step 4.If B is found ignore it and move left and goto step-8.
- Step-4: Keep ignoring Z, A, Y and D and move towards left.If X is found ignore it and move right and goto step-1.
- Step-5: Keep ignoring Y and move towards right. Ignore Z move left and goto step-11.If D is found make it Y and move right to step-6.
- Step-6: Keep ignoring D and Z and move towards right.Convert C into Z and move left and goto step-7.
- Step-7: Keep ignoring D and Z and move towards left.If Y is found ignore it and move right and goto step-5.
- Step-8: Keep ignoring D, Y and A and move towards left. Ignore X move right and goto step-9.
- Step-9: Convert A into X and move right and goto step-10.
- Step-10: Keep ignoring Y and A and move towards right.If B is found ignore it and move left and goto step-11.If D make it Y and move right and goto step-8.
- Step-11: Stop the Machine (String is accepted)
State transition diagram :
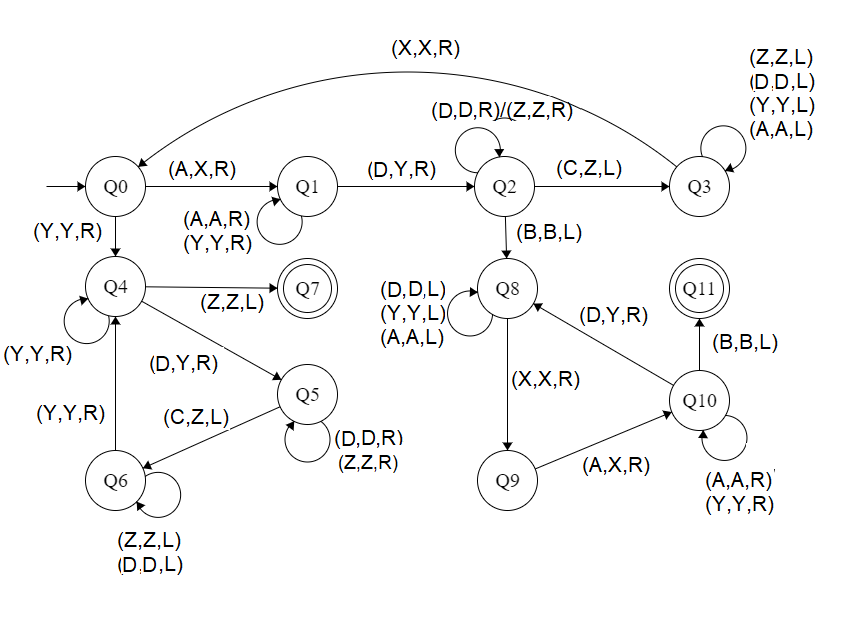
Here, Q0 shows the initial state and Q1, Q2, Q3, Q4, Q5, Q6, Q8, Q9, Q10 shows the transition state and Q7 and Q11 shows the final state. A, C, D are the variables used and R, L shows right and left.
Explanation:
- Using Q0, when A is found make it X and go to right and to state Q1.And, when Y is found ignore it and go to right and to state Q4
- On the state Q1, ignore all A and Y and goto right.If D found make it Y and goto right into next state Q2.
- In Q2, ignore all D, Z and move right.If B found ignore it, move left and goto the state Q4, If C found make it Z move left and to Q3.
- In Q3 state, ignore all Z, D, Y, A and move left.If X found ignore it move right to Q0.
- In Q4, ignore all Y and move right.If Z found ignore it move left to state Q6.If D is found make it Y and move to right to Q5.
- In Q5 state, ignore all D, Z and move right.If C found make it Z move left to state Q6
- In Q6, ignore all D, Z and move left.If Y found ignore it and move right to state Q4.
- If Q7 state is reached it will produced the result of acceptance of string.
- In Q8, ignore all A, Y, D and move left.If X found ignore it move right to state Q9.
- In Q9 state, if A found make it X move right to state Q10
- In Q10, ignore all A, Y and move right.If D found make it Y and move right to state Q8.If B is found ignore it and move left to Q11
- If Q11 state is reached it will produced the result of acceptance of string.
Note: For comparison of |A|, |D|, |C|, the concept of Turing Machine as Comparator is used
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...