Skip to content
Related Articles

Related Articles

Multistage Graph (Shortest Path)

View Discussion
Improve Article
Save Article
View Discussion
Improve Article
Save Article

A Multistage graph is a directed, weighted graph in which the nodes can be divided into a set of stages such that all edges are from a stage to next stage only (In other words there is no edge between vertices of same stage and from a vertex of current stage to previous stage).

The vertices of a multistage graph are divided into n number of disjoint subsets S = { S1 , S2 , S3 ……….. Sn },  where S1 is the source and Sn is the sink ( destination ). The cardinality of S1 and Sn are equal to 1. i.e., |S1| = |Sn| = 1.
We are given a multistage graph, a source and a destination, we need to find shortest path from source to destination. By convention, we consider source at stage 1 and destination as last stage.
Following is an example graph we will consider in this article :-
 

 

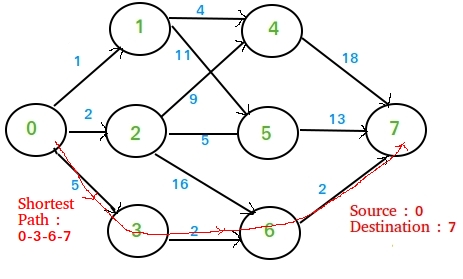
Now there are various strategies we can apply :-

  • The Brute force method of finding all possible paths between Source and Destination and then finding the minimum. That’s the WORST possible strategy.
  • Dijkstra’s Algorithm of Single Source shortest paths. This method will find shortest paths from source to all other nodes which is not required in this case. So it will take a lot of time and it doesn’t even use the SPECIAL feature that this MULTI-STAGE graph has.
  • Simple Greedy Method – At each node, choose the shortest outgoing path. If we apply this approach to the example graph give above we get the solution as 1 + 4 + 18 = 23. But a quick look at the graph will show much shorter paths available than 23. So the greedy method fails !
  • The best option is Dynamic Programming. So we need to find Optimal Sub-structure, Recursive Equations and Overlapping Sub-problems.

Optimal Substructure and Recursive Equation :- 
We define the notation :- M(x, y) as the minimum cost to T(target node) from Stage x, Node y. 
 

Shortest distance from stage 1, node 0 to 
destination, i.e., 7 is M(1, 0).

// From 0, we can go to 1 or 2 or 3 to
// reach 7.              
M(1, 0) = min(1 + M(2, 1),
              2 + M(2, 2),
              5 + M(2, 3))

This means that our problem of 0 —> 7 is now sub-divided into 3 sub-problems :-
 

So if we have total 'n' stages and target
as T, then the stopping condition  will be :-
M(n-1, i) = i ---> T + M(n, T) = i ---> T

Recursion Tree and Overlapping Sub-Problems:- 
So, the hierarchy of M(x, y) evaluations will look something like this :-
 

In M(i, j), i is stage number and
j is node number

                   M(1, 0)
           /          |         \                             
          /           |          \                            
       M(2, 1)      M(2, 2)        M(2, 3)
    /      \        /     \         /    \
M(3, 4)  M(3, 5)  M(3, 4)  M(3, 5) M(3, 6)  M(3, 6)
 .         .       .       .          .        .
 .         .       .       .          .        .
 .         .       .       .          .        .

So, here we have drawn a very small part of the Recursion Tree and we can already see Overlapping Sub-Problems. We can largely reduce the number of M(x, y) evaluations using Dynamic Programming.
Implementation details: 
The below implementation assumes that nodes are numbered from 0 to N-1 from first stage (source) to last stage (destination). We also assume that the input graph is multistage. 

We use top to bottom approach, and use dist[] array to store the value of overlapping sub-problem.

dist[i] will store the value of minimum distance from node i to node n-1 (target node).

Therefore, dist[0] will store minimum distance between from source node to target node.
 

C++




// CPP program to find shortest distance
// in a multistage graph.
#include<bits/stdc++.h>
using namespace std;
 
#define N 8
#define INF INT_MAX
 
// Returns shortest distance from 0 to
// N-1.
int shortestDist(int graph[N][N]) {
 
    // dist[i] is going to store shortest
    // distance from node i to node N-1.
    int dist[N];
 
    dist[N-1] = 0;
 
    // Calculating shortest path for
    // rest of the nodes
    for (int i = N-2 ; i >= 0 ; i--)
    {
 
        // Initialize distance from i to
        // destination (N-1)
        dist[i] = INF;
 
        // Check all nodes of next stages
        // to find shortest distance from
        // i to N-1.
        for (int j = i ; j < N ; j++)
        {
            // Reject if no edge exists
            if (graph[i][j] == INF)
                continue;
 
            // We apply recursive equation to
            // distance to target through j.
            // and compare with minimum distance
            // so far.
            dist[i] = min(dist[i], graph[i][j] +
                                        dist[j]);
        }
    }
 
    return dist[0];
}
 
// Driver code
int main()
{
    // Graph stored in the form of an
    // adjacency Matrix
    int graph[N][N] =
      {{INF, 1, 2, 5, INF, INF, INF, INF},
       {INF, INF, INF, INF, 4, 11, INF, INF},
       {INF, INF, INF, INF, 9, 5, 16, INF},
       {INF, INF, INF, INF, INF, INF, 2, INF},
       {INF, INF, INF, INF, INF, INF, INF, 18},
       {INF, INF, INF, INF, INF, INF, INF, 13},
       {INF, INF, INF, INF, INF, INF, INF, 2},
      {INF, INF, INF, INF, INF, INF, INF, INF}};
 
    cout << shortestDist(graph);
    return 0;
}

Java



// Java program to find shortest distance
// in a multistage graph.
class GFG
{
 
    static int N = 8;
    static int INF = Integer.MAX_VALUE;
 
    // Returns shortest distance from 0 to
    // N-1.
    public static int shortestDist(int[][] graph)
    {
 
        // dist[i] is going to store shortest
        // distance from node i to node N-1.
        int[] dist = new int[N];
 
        dist[N - 1] = 0;
 
        // Calculating shortest path for
        // rest of the nodes
        for (int i = N - 2; i >= 0; i--)
        {
 
            // Initialize distance from i to
            // destination (N-1)
            dist[i] = INF;
 
            // Check all nodes of next stages
            // to find shortest distance from
            // i to N-1.
            for (int j = i; j < N; j++)
            {
                // Reject if no edge exists
                if (graph[i][j] == INF)
                {
                    continue;
                }
 
                // We apply recursive equation to
                // distance to target through j.
                // and compare with minimum distance
                // so far.
                dist[i] = Math.min(dist[i], graph[i][j]
                        + dist[j]);
            }
        }
 
        return dist[0];
    }
 
    // Driver code
    public static void main(String[] args)
    {
        // Graph stored in the form of an
        // adjacency Matrix
        int[][] graph = new int[][]{{INF, 1, 2, 5, INF, INF, INF, INF},
        {INF, INF, INF, INF, 4, 11, INF, INF},
        {INF, INF, INF, INF, 9, 5, 16, INF},
        {INF, INF, INF, INF, INF, INF, 2, INF},
        {INF, INF, INF, INF, INF, INF, INF, 18},
        {INF, INF, INF, INF, INF, INF, INF, 13},
        {INF, INF, INF, INF, INF, INF, INF, 2}};
 
        System.out.println(shortestDist(graph));
    }
}
 
// This code has been contributed by 29AjayKumar
Python3



# Python3 program to find shortest
# distance in a multistage graph.
 
# Returns shortest distance from
# 0 to N-1.
def shortestDist(graph):
    global INF
 
    # dist[i] is going to store shortest
    # distance from node i to node N-1.
    dist = [0] * N
 
    dist[N - 1] = 0
 
    # Calculating shortest path
    # for rest of the nodes
    for i in range(N - 2, -1, -1):
 
        # Initialize distance from 
        # i to destination (N-1)
        dist[i] = INF
 
        # Check all nodes of next stages
        # to find shortest distance from
        # i to N-1.
        for j in range(N):
             
            # Reject if no edge exists
            if graph[i][j] == INF:
                continue
 
            # We apply recursive equation to
            # distance to target through j.
            # and compare with minimum
            # distance so far.
            dist[i] = min(dist[i],
                          graph[i][j] + dist[j])
 
    return dist[0]
 
# Driver code
N = 8
INF = 999999999999
 
# Graph stored in the form of an
# adjacency Matrix
graph = [[INF, 1, 2, 5, INF, INF, INF, INF],
         [INF, INF, INF, INF, 4, 11, INF, INF],
         [INF, INF, INF, INF, 9, 5, 16, INF],
         [INF, INF, INF, INF, INF, INF, 2, INF],
         [INF, INF, INF, INF, INF, INF, INF, 18],
         [INF, INF, INF, INF, INF, INF, INF, 13],
         [INF, INF, INF, INF, INF, INF, INF, 2]]
 
print(shortestDist(graph))
 
# This code is contributed by PranchalK
C#



// C# program to find shortest distance
// in a multistage graph.
using System;
   
class GFG
{
    static int N = 8;
    static int INF = int.MaxValue;
       
    // Returns shortest distance from 0 to
    // N-1.
    public static int shortestDist(int[,] graph) {
       
        // dist[i] is going to store shortest
        // distance from node i to node N-1.
        int[] dist = new int[N];
       
        dist[N-1] = 0;
       
        // Calculating shortest path for
        // rest of the nodes
        for (int i = N-2 ; i >= 0 ; i--)
        {
       
            // Initialize distance from i to
            // destination (N-1)
            dist[i] = INF;
       
            // Check all nodes of next stages
            // to find shortest distance from
            // i to N-1.
            for (int j = i ; j < N ; j++)
            {
                // Reject if no edge exists
                if (graph[i,j] == INF)
                    continue;
       
                // We apply recursive equation to
                // distance to target through j.
                // and compare with minimum distance 
                // so far.
                dist[i] = Math.Min(dist[i], graph[i,j] +
                                            dist[j]);
            }
        }
       
        return dist[0];
    }
       
    // Driver code
    static void Main()
    {
        // Graph stored in the form of an
        // adjacency Matrix
        int[,] graph = new int[,]
          {{INF, 1, 2, 5, INF, INF, INF, INF},
           {INF, INF, INF, INF, 4, 11, INF, INF},
           {INF, INF, INF, INF, 9, 5, 16, INF},
           {INF, INF, INF, INF, INF, INF, 2, INF},
           {INF, INF, INF, INF, INF, INF, INF, 18},
           {INF, INF, INF, INF, INF, INF, INF, 13},
           {INF, INF, INF, INF, INF, INF, INF, 2}};
       
        Console.Write(shortestDist(graph));
    }
}
 
// This code is contributed by DrRoot_
Javascript



<script>
 
// JavaScript program to find shortest distance
// in a multistage graph.
 
let N = 8;
let INF = Number.MAX_VALUE;
 
// Returns shortest distance from 0 to
    // N-1.
function shortestDist(graph)
{
    // dist[i] is going to store shortest
        // distance from node i to node N-1.
        let dist = new Array(N);
  
        dist[N - 1] = 0;
  
        // Calculating shortest path for
        // rest of the nodes
        for (let i = N - 2; i >= 0; i--)
        {
  
            // Initialize distance from i to
            // destination (N-1)
            dist[i] = INF;
  
            // Check all nodes of next stages
            // to find shortest distance from
            // i to N-1.
            for (let j = i; j < N; j++)
            {
                // Reject if no edge exists
                if (graph[i][j] == INF)
                {
                    continue;
                }
  
                // We apply recursive equation to
                // distance to target through j.
                // and compare with minimum distance
                // so far.
                dist[i] = Math.min(dist[i], graph[i][j]
                        + dist[j]);
            }
        }
  
        return dist[0];
}
 
let graph = [[INF, 1, 2, 5, INF, INF, INF, INF],
         [INF, INF, INF, INF, 4, 11, INF, INF],
         [INF, INF, INF, INF, 9, 5, 16, INF],
         [INF, INF, INF, INF, INF, INF, 2, INF],
         [INF, INF, INF, INF, INF, INF, INF, 18],
         [INF, INF, INF, INF, INF, INF, INF, 13],
         [INF, INF, INF, INF, INF, INF, INF, 2]];
document.write(shortestDist(graph));
 
 
// This code is contributed by rag2127
 
</script>
Output: 
9
 
Time Complexity : O(n2)
 

My Personal Notes
arrow_drop_up
Previous
Find the Largest Cube formed by Deleting minimum Digits from a number
Next

Maximize array elements upto given number
Recommended Articles
Page :
Difference between the shortest and second shortest path in an Unweighted Bidirectional Graph
04, Aug 21
Shortest path from source to destination such that edge weights along path are alternatively increasing and decreasing
24, Apr 19
0-1 BFS (Shortest Path in a Binary Weight Graph)
23, Apr 17
Check if given path between two nodes of a graph represents a shortest paths
28, Nov 19
Shortest path in a graph from a source S to destination D with exactly K edges for multiple Queries
14, Feb 20
Shortest path with exactly k edges in a directed and weighted graph | Set 2
31, Jan 20
Shortest path in a directed graph by Dijkstra’s algorithm
12, Jun 20
Building an undirected graph and finding shortest path using Dictionaries in Python
20, Jun 20
Shortest path in a complement graph
02, Jul 20
Create a Graph by connecting divisors from N to M and find shortest path
24, Aug 20
Detect a negative cycle in a Graph using Shortest Path Faster Algorithm
30, Sep 20
1st to Kth shortest path lengths from node 1 to N in given Graph
12, Jul 21
Shortest Path in Directed Acyclic Graph
13, May 13
Monotonic shortest path from source to destination in Directed Weighted Graph
27, Jul 22
Shortest path in an unweighted graph
10, Apr 18
Multi Source Shortest Path in Unweighted Graph
07, Jun 18
Shortest Path in a weighted Graph where weight of an edge is 1 or 2
13, Mar 16
Shortest path with exactly k edges in a directed and weighted graph
19, Aug 14
Find all remaining vertices in Graph after marking shortest path for neighbours
17, Aug 22
Convert the undirected graph into directed graph such that there is no path of length greater than 1
05, Apr 19
Shortest Path Faster Algorithm
17, Mar 20
Shortest path on a Square
01, Feb 19
D'Esopo-Pape Algorithm : Single Source Shortest Path
30, Mar 20
Maximize shortest path between given vertices by adding a single edge
07, Aug 20
Article Contributed By :
https://media.geeksforgeeks.org/auth/avatar.png
Siddhant-Bajaj
@Siddhant-Bajaj
Vote for difficulty
Current difficulty :
Medium





Improved By :
Article Tags :
Practice Tags :
Report Issue

We use cookies to ensure you have the best browsing experience on our website. By using our site, you
acknowledge that you have read and understood our
Cookie Policy &
        Privacy Policy

Lightbox

Start Your Coding Journey Now!