Building an undirected graph and finding shortest path using Dictionaries in Python
Last Updated :
15 Dec, 2021
Prerequisites:
In this article, we will be looking at how to build an undirected graph and then find the shortest path between two nodes/vertex of that graph easily using dictionaries in Python Language.
Building a Graph using Dictionaries
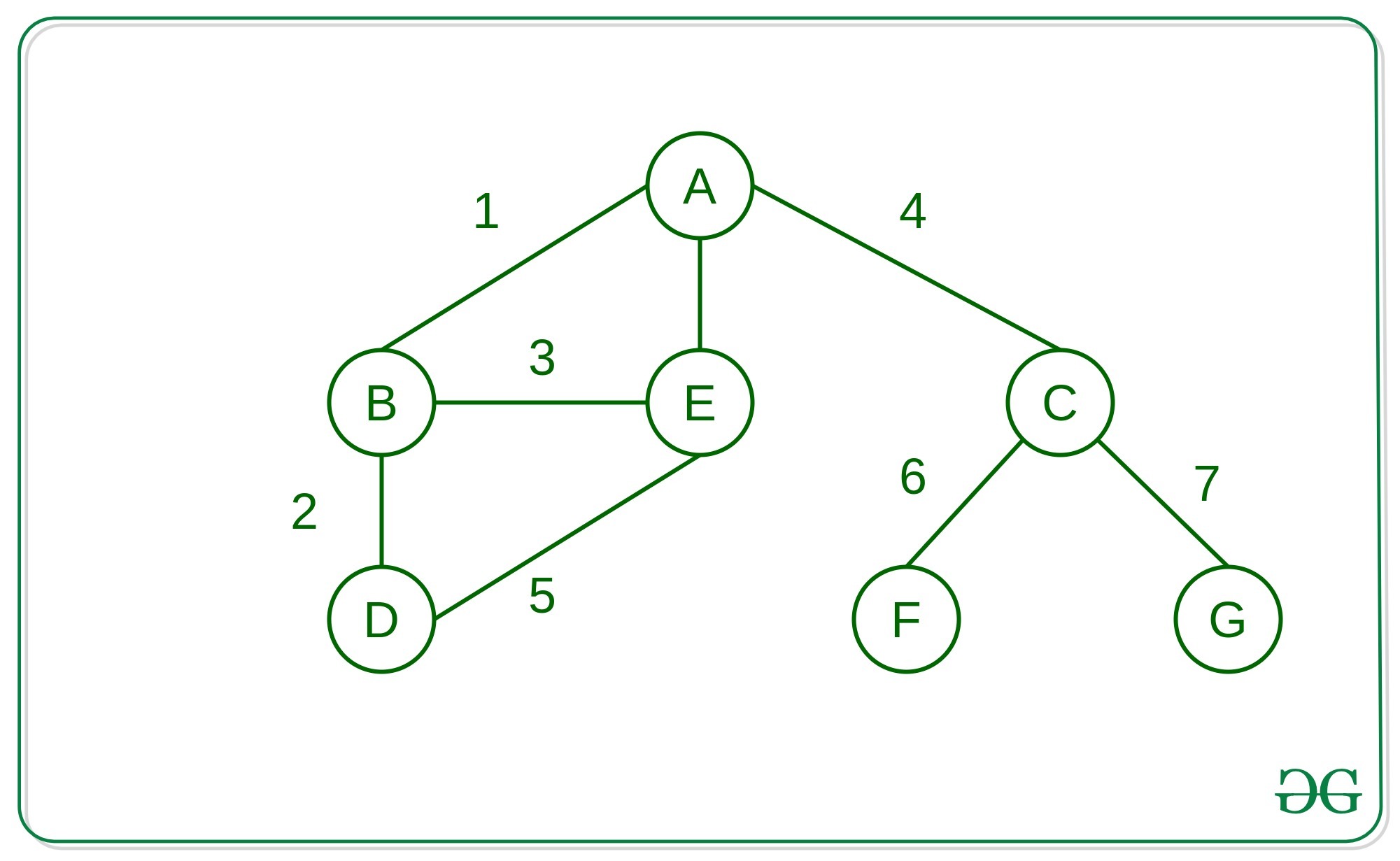
Approach: The idea is to store the adjacency list into the dictionaries, which helps to store the graph in any format not only in the form of the integers. Here we have used characters as a reference on those places any custom objects can also be used.
Below is the implementation of the above approach:
Python3
from collections import defaultdict
def build_graph():
edges = [
["A", "B"], ["A", "E"],
["A", "C"], ["B", "D"],
["B", "E"], ["C", "F"],
["C", "G"], ["D", "E"]
]
graph = defaultdict(list)
for edge in edges:
a, b = edge[0], edge[1]
graph[a].append(b)
graph[b].append(a)
return graph
if __name__ == "__main__":
graph = build_graph()
print(graph)
|
Output:
{
'G': ['C'],
'F': ['C'],
'E': ['A', 'B', 'D'],
'A': ['B', 'E', 'C'],
'B': ['A', 'D', 'E'],
'D': ['B', 'E'],
'C': ['A', 'F', 'G']
}
Shortest Path between two nodes of graph
Approach: The idea is to use queue and visit every adjacent node of the starting nodes that traverses the graph in Breadth-First Search manner to find the shortest path between two nodes of the graph.
Below is the implementation of the above approach:
Python3
def BFS_SP(graph, start, goal):
explored = []
queue = [[start]]
if start == goal:
print("Same Node")
return
while queue:
path = queue.pop(0)
node = path[-1]
if node not in explored:
neighbours = graph[node]
for neighbour in neighbours:
new_path = list(path)
new_path.append(neighbour)
queue.append(new_path)
if neighbour == goal:
print("Shortest path = ", *new_path)
return
explored.append(node)
print("So sorry, but a connecting"\
"path doesn't exist :(")
return
if __name__ == "__main__":
graph = {'A': ['B', 'E', 'C'],
'B': ['A', 'D', 'E'],
'C': ['A', 'F', 'G'],
'D': ['B', 'E'],
'E': ['A', 'B', 'D'],
'F': ['C'],
'G': ['C']}
BFS_SP(graph, 'A', 'D')
|
Output:
Shortest path = A B D
Share your thoughts in the comments
Please Login to comment...