Maximum sum rectangle in a 2D matrix | DP-27

Given a 2D array, find the maximum sum submatrix in it. For example, in the following 2D array, the maximum sum submatrix is highlighted with blue rectangle and sum of all elements in this submatrix is 29.

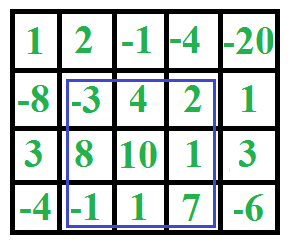
This problem is mainly an extension of Largest Sum Contiguous Subarray for 1D array.  

The Naive Solution for this problem is to check every possible rectangle in the given 2D array. This solution requires 6 nested loops –  

• 4 for start and end coordinate of the 2 axis O(n⁴)
• and 2 for the summation of the sub-matrix O(n²).

Below is the implementation of the above approach:

C++

#include <bits/stdc++.h>
using namespace std;

void maxMatrixSum(vector<vector<int> >& matrix)
{
    int n = matrix.size(); // no of rows in a matrix;
    int m = matrix[0].size(); // no of columns in matrix;
    int maxsum = INT_MIN;
    int top = 0, bottom = 0, left = 0, right = 0;
    // a loop for top row position in  the
    // rectangle
    for (int i = 0; i < n; i++) {
        // a loop for  left column position
        // of the rectangle
        for (int j = 0; j < m; j++) {
            // a loop for bottom  row in the
            // rectangle
            for (int k = 0; k < n; k++) {
                for (int l = 0; l < m; l++) {
                    // a loop for right column in
                    // the rectangle
                    int curr = 0;
                    for (int x = i; x <= k; x++) {
                        // a loops execute for
                        // finding sum of elements in the
                        // rectangle
                        for (int y = j; y <= l; y++) {
                            // for all possibble
                            // points of rectangle
                            curr += matrix[x][y];
                        }
                    }
                  // updating the resultant variables if curr > maxsum
                    if (curr > maxsum) {
                        maxsum = curr;
                        top = i;
                        left = j;
                        right = k;
                        bottom = l;
                    }
                }
            }
        }
    }
    cout << "( Top , Left )"
         << "( " << top << " , " << left << " )" << endl;
    cout << "( Bottom , Right )"
         << "( " << bottom << " , " << right << " )"
         << endl;
    cout << "The sum of this rectangle is: " << maxsum
         << endl;
}
int main()
{
    vector<vector<int> > v = { { 1, 2, -1, -4, -20 },
                               { -8, -3, 4, 2, 1 },
                               { 3, 8, 10, 1, 3 },
                               { -4, -1, 1, 7, -6 } };
    maxMatrixSum(v);
    return 0;
}
// contributed by hungry_coder_109(Naveen);

Java

import java.io.*;
import java.lang.*;
import java.util.*;
class GFG {
    public static void maxMatrixSum(int[][] matrix)
    {
        int n = matrix.length; // no of rows in a matrix;
        int m
            = matrix[0].length; // no of columns in matrix;
        int maxsum = -999999999;
        int top = 0, bottom = 0, left = 0, right = 0;
        for (int i = 0; i < n;
             i++) { // This loop for top row position in the
                    // rectangle
            for (int j = 0; j < m;
                 j++) { // This loop for  left column
                        // position of the rectangle
                for (int k = 0; k < n;
                     k++) { // This loop for bottom  row in
                            // the rectangle
                    for (int l = 0; l < m;
                         l++) { // This loop for right
                                // column in the rectangle

                        int curr = 0;
                        for (int x = i; x <= k;
                             x++) { // This  loops execute
                                    // for finding sum of
                                    // elements in the
                                    // rectangle
                            for (int y = j; y <= l;
                                 y++) { // for all possibble
                                        // points of
                                        // rectangle
                                curr += matrix[x][y];
                            }
                        }
                        if (curr > maxsum) {
                            maxsum = curr;
                            top = i;
                            left = j;
                            right = k;
                            bottom = l;
                        }
                    }
                }
            }
        }
        System.out.println("Top , Left ) ( " + top + " , "
                           + left + " )");
        System.out.println("Bottom , Right) ( " + bottom
                           + " , " + right + " )");
        System.out.println("The sum of the rectangle is: "
                           + maxsum);
    }
    public static void main(String[] args)
    {
        int arr[][] = new int[][] { { 1, 2, -1, -4, -20 },
                                    { -8, -3, 4, 2, 1 },
                                    { 3, 8, 10, 1, 3 },
                                    { -4, -1, 1, 7, -6 } };

        // Function call
        maxMatrixSum(arr);
    }
}
// contributed by hungry_coder_109(Naveen);

Python3

def max_matrix_sum(matrix):
    n = len(matrix)  # number of rows in the matrix
    m = len(matrix[0])  # number of columns in the matrix
    max_sum = float('-inf')
    top = 0
    bottom = 0
    left = 0
    right = 0

    # Loop for top row position in the rectangle
    for i in range(n):
        # Loop for left column position of the rectangle
        for j in range(m):
            # Loop for bottom row in the rectangle
            for k in range(n):
                # Loop for right column in the rectangle
                for l in range(m):
                    curr = 0
                    # Loop to find the sum of elements in the rectangle
                    for x in range(i, k+1):
                        # Loop for all possible points of the rectangle
                        for y in range(j, l+1):
                            curr += matrix[x][y]
                    # Update the result variables if curr > max_sum
                    if curr > max_sum:
                        max_sum = curr
                        top = i
                        left = j
                        right = l
                        bottom = k

    print("(Top, Left): ({}, {})".format(top, left))
    print("(Bottom, Right): ({}, {})".format(bottom, right))
    print("The sum of this rectangle is:", max_sum)

matrix = [[1, 2, -1, -4, -20],
          [-8, -3, 4, 2, 1],
          [3, 8, 10, 1, 3],
          [-4, -1, 1, 7, -6]]

max_matrix_sum(matrix)

C#

using System;

class GFG {
    // Function to find the maximum sum subrectangle in a
    // given matrix
    static void MaxMatrixSum(int[][] matrix)
    {
        int n
            = matrix.Length; // Number of rows in the matrix
        int m = matrix[0].Length; // Number of columns in
                                  // the matrix
        int maxsum
            = int.MinValue; // Variable to store the maximum
                            // sum found so far
        int top = 0, bottom = 0, left = 0,
            right
            = 0; // Variables to store the coordinates of
                 // the subrectangle with the maximum sum

        // Loop for the top row position of the rectangle
        for (int i = 0; i < n; i++) {
            // Loop for the left column position of the
            // rectangle
            for (int j = 0; j < m; j++) {
                // Loop for the bottom row position of the
                // rectangle
                for (int k = i; k < n; k++) {
                    // Loop for the right column position of
                    // the rectangle
                    for (int l = j; l < m; l++) {
                        int curr
                            = 0; // Variable to store the
                                 // current sum of elements
                                 // in the rectangle

                        // Nested loops execute for finding
                        // the sum of elements in the
                        // rectangle
                        for (int x = i; x <= k; x++) {
                            for (int y = j; y <= l; y++) {
                                curr += matrix[x][y];
                            }
                        }

                        // Updating the resultant variables
                        // if curr > maxsum
                        if (curr > maxsum) {
                            maxsum = curr;
                            top = i;
                            left = j;
                            right = l;
                            bottom = k;
                        }
                    }
                }
            }
        }

        // Printing the coordinates and sum of the maximum
        // sum subrectangle
        Console.WriteLine("(Top, Left) (" + top + ", "
                          + left + ")");
        Console.WriteLine("(Bottom, Right) (" + bottom
                          + ", " + right + ")");
        Console.WriteLine("The sum of this rectangle is: "
                          + maxsum);
    }

    static void Main()
    {
        int[][] v
            = new int[][] { new int[] { 1, 2, -1, -4, -20 },
                            new int[] { -8, -3, 4, 2, 1 },
                            new int[] { 3, 8, 10, 1, 3 },
                            new int[] { -4, -1, 1, 7,
                                        -6 } };

        MaxMatrixSum(v);
    }
}

Javascript

function maxMatrixSum(matrix) {
    const n = matrix.length;
    const m = matrix[0].length;
    let maxsum = Number.MIN_SAFE_INTEGER;
    let top = 0, bottom = 0, left = 0, right = 0;
    // A loop for the top row position in
    // the rectangle
    for (let i = 0; i < n; i++) {
        // A loop for the left column
        // position of the rectangle
        for (let j = 0; j < m; j++) {
            for (let k = i; k < n; k++) {
                for (let l = j; l < m; l++) {
                    let curr = 0;
                    // Loop to calculate the sum of
                    // elements in the rectangle
                    for (let x = i; x <= k; x++) {
                        for (let y = j; y <= l; y++) {
                            curr += matrix[x][y];
                        }
                    }
                    // Update the result variables if curr > maxsum
                    if (curr > maxsum) {
                        maxsum = curr;
                        top = i;
                        left = j;
                        bottom = k;
                        right = l;
                    }
                }
            }
        }
    }
    console.log(`( Top , Left ) ( ${top} , ${left} )`);
    console.log(`( Bottom , Right ) ( ${bottom} , ${right} )`);
    console.log(`The sum of this rectangle is: ${maxsum}`);
}
const matrix = [
    [1, 2, -1, -4, -20],
    [-8, -3, 4, 2, 1],
    [3, 8, 10, 1, 3],
    [-4, -1, 1, 7, -6]
];
maxMatrixSum(matrix);

Output:

( Top , Left )( 1 , 1 )

( Bottom , Right )( 3 , 3 )

The sum of this rectangle is: 29

Time Complexity: O(n^3 * m^3) where n is the number of rows and m is the numbr of columns in the given matrix.

Efficient Approach – 

Kadane’s algorithm for 1D array can be used to reduce the time complexity to O(n^3). The idea is to fix the left and right columns one by one and find the maximum sum contiguous rows for every left and right column pair. We basically find top and bottom row numbers (which have maximum sum) for every fixed left and right column pair. To find the top and bottom row numbers, calculate the sum of elements in every row from left to right and store these sums in an array say temp[]. So temp[i] indicates sum of elements from left to right in row i. If we apply Kadane’s 1D algorithm on temp[], and get the maximum sum subarray of temp, this maximum sum would be the maximum possible sum with left and right as boundary columns. To get the overall maximum sum, we compare this sum with the maximum sum so far.

Implementation:

C++

// Program to find maximum sum subarray
// in a given 2D array
#include <bits/stdc++.h>
using namespace std;

#define ROW 4
#define COL 5

// Implementation of Kadane's algorithm for
// 1D array. The function returns the maximum
// sum and stores starting and ending indexes
// of the maximum sum subarray at addresses
// pointed by start and finish pointers
// respectively.
int kadane(int* arr, int* start, int* finish, int n)
{
    // initialize sum, maxSum and
    int sum = 0, maxSum = INT_MIN, i;

    // Just some initial value to check
    // for all negative values case
    *finish = -1;

    // local variable
    int local_start = 0;

    for (i = 0; i < n; ++i) {
        sum += arr[i];
        if (sum < 0) {
            sum = 0;
            local_start = i + 1;
        }
        else if (sum > maxSum) {
            maxSum = sum;
            *start = local_start;
            *finish = i;
        }
    }

    // There is at-least one
    // non-negative number
    if (*finish != -1)
        return maxSum;

    // Special Case: When all numbers
    // in arr[] are negative
    maxSum = arr[0];
    *start = *finish = 0;

    // Find the maximum element in array
    for (i = 1; i < n; i++) {
        if (arr[i] > maxSum) {
            maxSum = arr[i];
            *start = *finish = i;
        }
    }
    return maxSum;
}

// The main function that finds
// maximum sum rectangle in M[][]
void findMaxSum(int M[][COL])
{
    // Variables to store the final output
    int maxSum = INT_MIN, finalLeft, finalRight, finalTop,
        finalBottom;

    int left, right, i;
    int temp[ROW], sum, start, finish;

    // Set the left column
    for (left = 0; left < COL; ++left) {
        // Initialize all elements of temp as 0
        memset(temp, 0, sizeof(temp));

        // Set the right column for the left
        // column set by outer loop
        for (right = left; right < COL; ++right) {

            // Calculate sum between current left
            // and right for every row 'i'
            for (i = 0; i < ROW; ++i)
                temp[i] += M[i][right];

            // Find the maximum sum subarray in temp[].
            // The kadane() function also sets values
            // of start and finish. So 'sum' is sum of
            // rectangle between (start, left) and
            // (finish, right) which is the maximum sum
            // with boundary columns strictly as left
            // and right.
            sum = kadane(temp, &start, &finish, ROW);

            // Compare sum with maximum sum so far.
            // If sum is more, then update maxSum and
            // other output values
            if (sum > maxSum) {
                maxSum = sum;
                finalLeft = left;
                finalRight = right;
                finalTop = start;
                finalBottom = finish;
            }
        }
    }

    // Print final values
    cout << "(Top, Left) (" << finalTop << ", " << finalLeft
         << ")" << endl;
    cout << "(Bottom, Right) (" << finalBottom << ", "
         << finalRight << ")" << endl;
    cout << "Max sum is: " << maxSum << endl;
}

// Driver Code
int main()
{
    int M[ROW][COL] = { { 1, 2, -1, -4, -20 },
                        { -8, -3, 4, 2, 1 },
                        { 3, 8, 10, 1, 3 },
                        { -4, -1, 1, 7, -6 } };

    // Function call
    findMaxSum(M);

    return 0;
}

// This code is contributed by
// rathbhupendra

C

// Program to find maximum sum subarray
// in a given 2D array
#include <limits.h>
#include <stdio.h>
#include <string.h>
#define ROW 4
#define COL 5

// Implementation of Kadane's algorithm
// for 1D array. The function returns the
// maximum sum and stores starting and
// ending indexes of the maximum sum subarray
// at addresses pointed by start and finish
// pointers respectively.
int kadane(int* arr, int* start, int* finish, int n)
{
    // initialize sum, maxSum and
    int sum = 0, maxSum = INT_MIN, i;

    // Just some initial value to check for all negative
    // values case
    *finish = -1;

    // local variable
    int local_start = 0;

    for (i = 0; i < n; ++i) {
        sum += arr[i];
        if (sum < 0) {
            sum = 0;
            local_start = i + 1;
        }
        else if (sum > maxSum) {
            maxSum = sum;
            *start = local_start;
            *finish = i;
        }
    }

    // There is at-least one non-negative number
    if (*finish != -1)
        return maxSum;

    // Special Case: When all numbers in arr[]
    // are negative
    maxSum = arr[0];
    *start = *finish = 0;

    // Find the maximum element in array
    for (i = 1; i < n; i++) {
        if (arr[i] > maxSum) {
            maxSum = arr[i];
            *start = *finish = i;
        }
    }
    return maxSum;
}

// The main function that finds maximum
// sum rectangle in
// M[][]
void findMaxSum(int M[][COL])
{
    // Variables to store the final output
    int maxSum = INT_MIN, finalLeft, finalRight, finalTop,
        finalBottom;

    int left, right, i;
    int temp[ROW], sum, start, finish;

    // Set the left column
    for (left = 0; left < COL; ++left) {
        // Initialize all elements of temp as 0
        memset(temp, 0, sizeof(temp));

        // Set the right column for the left column set by
        // outer loop
        for (right = left; right < COL; ++right) {
            // Calculate sum between current left and right
            // for every row 'i'
            for (i = 0; i < ROW; ++i)
                temp[i] += M[i][right];

            // Find the maximum sum subarray in temp[].
            // The kadane() function also sets values of
            // start and finish.  So 'sum' is sum of
            // rectangle between (start, left) and (finish,
            //  right) which is the maximum sum with
            //  boundary columns strictly as left and right.
            sum = kadane(temp, &start, &finish, ROW);

            // Compare sum with maximum sum so far. If sum
            // is more, then update maxSum and other output
            // values
            if (sum > maxSum) {
                maxSum = sum;
                finalLeft = left;
                finalRight = right;
                finalTop = start;
                finalBottom = finish;
            }
        }
    }

    // Print final values
    printf("(Top, Left) (%d, %d)\n", finalTop, finalLeft);
    printf("(Bottom, Right) (%d, %d)\n", finalBottom,
           finalRight);
    printf("Max sum is: %d\n", maxSum);
}

// Driver Code
int main()
{
    int M[ROW][COL] = { { 1, 2, -1, -4, -20 },
                        { -8, -3, 4, 2, 1 },
                        { 3, 8, 10, 1, 3 },
                        { -4, -1, 1, 7, -6 } };

    // Function call
    findMaxSum(M);

    return 0;
}

Java

// Java Program to find max sum rectangular submatrix

import java.io.*;
import java.lang.*;
import java.util.*;

class MaximumSumRectangle {

    // Function to find maximum sum rectangular
    // submatrix
    private static int maxSumRectangle(int[][] mat)
    {
        int m = mat.length;
        int n = mat[0].length;
        int preSum[][] = new int[m + 1][n];

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                preSum[i + 1][j] = preSum[i][j] + mat[i][j];
            }
        }

        int maxSum = -1;
        int minSum = Integer.MIN_VALUE;
        int negRow = 0, negCol = 0;
        int rStart = 0, rEnd = 0, cStart = 0, cEnd = 0;
        for (int rowStart = 0; rowStart < m; rowStart++) {
            for (int row = rowStart; row < m; row++) {
                int sum = 0;
                int curColStart = 0;
                for (int col = 0; col < n; col++) {
                    sum += preSum[row + 1][col]
                           - preSum[rowStart][col];
                    if (sum < 0) {
                        if (minSum < sum) {
                            minSum = sum;
                            negRow = row;
                            negCol = col;
                        }
                        sum = 0;
                        curColStart = col + 1;
                    }
                    else if (maxSum < sum) {
                        maxSum = sum;
                        rStart = rowStart;
                        rEnd = row;
                        cStart = curColStart;
                        cEnd = col;
                    }
                }
            }
        }

        // Printing final values
        if (maxSum == -1) {
            System.out.println("from row - " + negRow
                               + " to row - " + negRow);
            System.out.println("from col - " + negCol
                               + " to col - " + negCol);
        }
        else {
            System.out.println("from row - " + rStart
                               + " to row - " + rEnd);
            System.out.println("from col - " + cStart
                               + " to col - " + cEnd);
        }
        return maxSum == -1 ? minSum : maxSum;
    }

    // Driver Code
    public static void main(String[] args)
    {
        int arr[][] = new int[][] { { 1, 2, -1, -4, -20 },
                                    { -8, -3, 4, 2, 1 },
                                    { 3, 8, 10, 1, 3 },
                                    { -4, -1, 1, 7, -6 } };

        // Function call
        System.out.println(maxSumRectangle(arr));
    }
}

// This code is contributed by Nayanava De

Python3

# Python3 program to find maximum sum
# subarray in a given 2D array

# Implementation of Kadane's algorithm
# for 1D array. The function returns the
# maximum sum and stores starting and
# ending indexes of the maximum sum subarray
# at addresses pointed by start and finish
# pointers respectively.


def kadane(arr, start, finish, n):

    # initialize sum, maxSum and
    Sum = 0
    maxSum = -999999999999
    i = None

    # Just some initial value to check
    # for all negative values case
    finish[0] = -1

    # local variable
    local_start = 0

    for i in range(n):
        Sum += arr[i]
        if Sum < 0:
            Sum = 0
            local_start = i + 1
        elif Sum > maxSum:
            maxSum = Sum
            start[0] = local_start
            finish[0] = i

    # There is at-least one
    # non-negative number
    if finish[0] != -1:
        return maxSum

    # Special Case: When all numbers
    # in arr[] are negative
    maxSum = arr[0]
    start[0] = finish[0] = 0

    # Find the maximum element in array
    for i in range(1, n):
        if arr[i] > maxSum:
            maxSum = arr[i]
            start[0] = finish[0] = i
    return maxSum

# The main function that finds maximum
# sum rectangle in M[][]


def findMaxSum(M):
    global ROW, COL

    # Variables to store the final output
    maxSum, finalLeft = -999999999999, None
    finalRight, finalTop, finalBottom = None, None, None
    left, right, i = None, None, None

    temp = [None] * ROW
    Sum = 0
    start = [0]
    finish = [0]

    # Set the left column
    for left in range(COL):

        # Initialize all elements of temp as 0
        temp = [0] * ROW

        # Set the right column for the left
        # column set by outer loop
        for right in range(left, COL):

            # Calculate sum between current left
            # and right for every row 'i'
            for i in range(ROW):
                temp[i] += M[i][right]

            # Find the maximum sum subarray in
            # temp[]. The kadane() function also
            # sets values of start and finish.
            # So 'sum' is sum of rectangle between
            # (start, left) and (finish, right) which
            # is the maximum sum with boundary columns
            # strictly as left and right.
            Sum = kadane(temp, start, finish, ROW)

            # Compare sum with maximum sum so far.
            # If sum is more, then update maxSum
            # and other output values
            if Sum > maxSum:
                maxSum = Sum
                finalLeft = left
                finalRight = right
                finalTop = start[0]
                finalBottom = finish[0]

    # Prfinal values
    print("(Top, Left)", "(", finalTop,
          finalLeft, ")")
    print("(Bottom, Right)", "(", finalBottom,
          finalRight, ")")
    print("Max sum is:", maxSum)


# Driver Code
ROW = 4
COL = 5
M = [[1, 2, -1, -4, -20],
     [-8, -3, 4, 2, 1],
     [3, 8, 10, 1, 3],
     [-4, -1, 1, 7, -6]]

# Function call
findMaxSum(M)

# This code is contributed by PranchalK

C#

// C# Given a 2D array, find the
// maximum sum subarray in it
using System;

class GFG {

    /**
     * To find maxSum in 1d array
     *
     * return {maxSum, left, right}
     */
    public static int[] kadane(int[] a)
    {
        int[] result = new int[] { int.MinValue, 0, -1 };
        int currentSum = 0;
        int localStart = 0;

        for (int i = 0; i < a.Length; i++) {
            currentSum += a[i];
            if (currentSum < 0) {
                currentSum = 0;
                localStart = i + 1;
            }
            else if (currentSum > result[0]) {
                result[0] = currentSum;
                result[1] = localStart;
                result[2] = i;
            }
        }

        // all numbers in a are negative
        if (result[2] == -1) {
            result[0] = 0;
            for (int i = 0; i < a.Length; i++) {
                if (a[i] > result[0]) {
                    result[0] = a[i];
                    result[1] = i;
                    result[2] = i;
                }
            }
        }
        return result;
    }

    /**
    * To find and print maxSum,
     (left, top),(right, bottom)
    */
    public static void findMaxSubMatrix(int[, ] a)
    {
        int cols = a.GetLength(1);
        int rows = a.GetLength(0);
        int[] currentResult;
        int maxSum = int.MinValue;
        int left = 0;
        int top = 0;
        int right = 0;
        int bottom = 0;

        for (int leftCol = 0; leftCol < cols; leftCol++) {
            int[] tmp = new int[rows];

            for (int rightCol = leftCol; rightCol < cols;
                 rightCol++) {

                for (int i = 0; i < rows; i++) {
                    tmp[i] += a[i, rightCol];
                }
                currentResult = kadane(tmp);
                if (currentResult[0] > maxSum) {
                    maxSum = currentResult[0];
                    left = leftCol;
                    top = currentResult[1];
                    right = rightCol;
                    bottom = currentResult[2];
                }
            }
        }

        Console.Write("MaxSum: " + maxSum + ", range: [("
                      + left + ", " + top + ")(" + right
                      + ", " + bottom + ")]");
    }

    // Driver Code
    public static void Main()
    {
        int[, ] arr = { { 1, 2, -1, -4, -20 },
                        { -8, -3, 4, 2, 1 },
                        { 3, 8, 10, 1, 3 },
                        { -4, -1, 1, 7, -6 } };

        // Function call
        findMaxSubMatrix(arr);
    }
}

// This code is contributed
// by PrinciRaj1992

Javascript

<script>

// Program to find maximum sum subarray
// in a given 2D array

var ROW = 4
var COL = 5
var start = 0
var finish = 0

// Implementation of Kadane's algorithm for
// 1D array. The function returns the maximum
// sum and stores starting and ending indexes
// of the maximum sum subarray at addresses
// pointed by start and finish pointers
// respectively.
function kadane(arr, n)
{
    // initialize sum, maxSum and
    var sum = 0, maxSum = -1000000000, i;

    // Just some initial value to check
    // for all negative values case
    finish = -1;

    // local variable
    var local_start = 0;

    for (i = 0; i < n; ++i)
    {
        sum += arr[i];
        if (sum < 0)
        {
            sum = 0;
            local_start = i + 1;
        }
        else if (sum > maxSum)
        {
            maxSum = sum;
            start = local_start;
            finish = i;
        }
    }

    // There is at-least one
    // non-negative number
    if (finish != -1)
        return maxSum;

    // Special Case: When all numbers
    // in arr[] are negative
    maxSum = arr[0];
    start = finish = 0;

    // Find the maximum element in array
    for (i = 1; i < n; i++)
    {
        if (arr[i] > maxSum)
        {
            maxSum = arr[i];
            start = finish = i;
        }
    }
    return maxSum;
}

// The main function that finds
// maximum sum rectangle in M[][]
function findMaxSum(M)
{
    // Variables to store the final output
    var maxSum = -1000000000,
                 finalLeft=0,
                 finalRight=0,
                 finalTop=0,
                 finalBottom=0;

    var left, right, i;
    var temp = Array(ROW);
    var sum;

    // Set the left column
    for (left = 0; left < COL; ++left) {
        // Initialize all elements of temp as 0
        temp = Array(ROW).fill(0);

        // Set the right column for the left
        // column set by outer loop
        for (right = left; right < COL; ++right) {

            // Calculate sum between current left
            // and right for every row 'i'
            for (i = 0; i < ROW; ++i)
                temp[i] += M[i][right];

            // Find the maximum sum subarray in temp[].
            // The kadane() function also sets values
            // of start and finish. So 'sum' is sum of
            // rectangle between (start, left) and
            // (finish, right) which is the maximum sum
            // with boundary columns strictly as left
            // and right.
            sum = kadane(temp, ROW);

            // Compare sum with maximum sum so far.
            // If sum is more, then update maxSum and
            // other output values
            if (sum > maxSum) {
                maxSum = sum;
                finalLeft = left;
                finalRight = right;
                finalTop = start;
                finalBottom = finish;
            }
        }
    }

    // Print final values
    document.write("(Top, Left) ("
         + finalTop + ", "
         + finalLeft
         + ")" + "<br>");
    document.write("(Bottom, Right) ("
         + finalBottom + ", "
         + finalRight + ")" + "<br>");
    document.write("Max sum is: " + maxSum + "<br>");
}

// Driver Code
var M = [ [ 1, 2, -1, -4, -20 ],
                    [ -8, -3, 4, 2, 1 ],
                    [ 3, 8, 10, 1, 3 ],
                    [ -4, -1, 1, 7, -6 ] ];
// Function call
findMaxSum(M);

// This code is contributed by rutvik_56.
</script>

Output

(Top, Left) (1, 1)
(Bottom, Right) (3, 3)
Max sum is: 29

Time Complexity: O(c*c*r), where c represents the number of columns and r represents the number of rows in the given matrix.
Auxiliary Space: O(r), where r represents the number of rows in the given matrix.