Maximum area of a Rectangle that can be circumscribed about a given Rectangle of size LxW

Given a rectangle of dimensions L and W. The task is to find the maximum area of a rectangle that can be circumscribed about a given rectangle with dimensions L and W.

Examples:

Input: L = 10, W = 10
Output: 200

Input: L = 18, W = 12
Output: 450

Approach: Let below is the given rectangle EFGH of dimensions L and W. We have to find the area of rectangle ABCD which is circumscribing rectangle EFGH. 

In the above figure: 
If 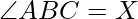then 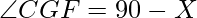as GCF is right angled triangle. 
Therefore, 

=> 
=> 
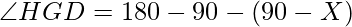
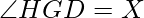
Similarly, 


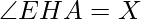
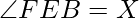
Now, The area of rectangle ABCD is given by: 

Area = AB * AD 
Area = (AE + EB)*(AH + HD) …..(1) 

According to the projection rule: 
AE = L*sin(X) 
EB = W*cos(X) 
AH = L*cos(X) 
HD = W*sin(X) 

Substituting the value of the above projections in equation (1) we have: 

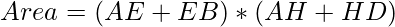
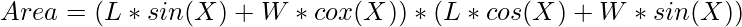
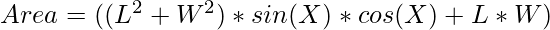
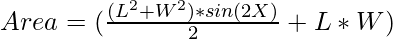
Now to maximize the area, the value of sin(2X) must be maximum i.e., 1. 
Therefore after substituting sin(2X) as 1 we have, 

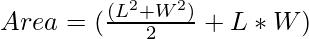
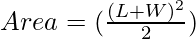
Below is the implementation of the above approach: 

C++

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;

// Function to find area of rectangle
// inscribed another rectangle of
// length L and width W
double AreaofRectangle(int L, int W)
{

    // Area of rectangle
    double area = (W + L) * (W + L) / 2;

    // Return the area
    return area;
}

// Driver Code
int main()
{

    // Given dimensions
    int L = 18;
    int W = 12;

    // Function call
    cout << AreaofRectangle(L, W);
    return 0;
}

// This code is contributed by Princi Singh

Java

// Java program for the above approach
import java.io.*;
import java.util.*;

class GFG{

// Function to find area of rectangle
// inscribed another rectangle of
// length L and width W
static double AreaofRectangle(int L, int W)
{

    // Area of rectangle
    double area = (W + L) * (W + L) / 2;

    // Return the area
    return area;
}

// Driver Code
public static void main(String args[])
{

    // Given dimensions
    int L = 18;
    int W = 12;

    // Function call
    System.out.println(AreaofRectangle(L, W));
}
}

// This code is contributed by offbeat

Python3

# Python3 program for the above approach

# Function to find area of rectangle
# inscribed another rectangle of
# length L and width W
def AreaofRectangle(L, W):

  # Area of rectangle
  area =(W + L)*(W + L)/2

# Return the area
  return area

# Driver Code
if __name__ == "__main__":

  # Given Dimensions
  L = 18
  W = 12

  # Function Call
  print(AreaofRectangle(L, W))

C#

// C# program for the above approach
using System;

class GFG{

// Function to find area of rectangle
// inscribed another rectangle of
// length L and width W
static double AreaofRectangle(int L, int W)
{

    // Area of rectangle
    double area = (W + L) * (W + L) / 2;

    // Return the area
    return area;
}

// Driver Code
public static void Main(String []args)
{

    // Given dimensions
    int L = 18;
    int W = 12;

    // Function call
    Console.Write(AreaofRectangle(L, W));
}
}

// This code is contributed by shivanisinghss2110

Javascript

<script>
      // JavaScript program for the above approach

      // Function to find area of rectangle
      // inscribed another rectangle of
      // length L and width W
      function AreaofRectangle(L, W) {
        // Area of rectangle
        var area = parseFloat(((W + L) * (W + L)) / 2).toFixed(1);

        // Return the area
        return area;
      }

      // Driver Code
      // Given dimensions
      var L = 18;
      var W = 12;

      // Function call
      document.write(AreaofRectangle(L, W));
    </script>

Output:

450.0

Time Complexity: O(1)
Auxiliary Space: O(1)