Count ways to reach target cell in a rectangle with restricted sub-rectangle

Given a grid of size M x N and two integers X and Y. A restricted area is defined as the lower left sub-rectangle consisting of X x Y blocks. Starting from the upper left cell find the number of ways to reach the bottom right cell where a legal move is defined to move right or down but never into the restricted area or outside the given grid.  Note: As the number of ways can be very large output the answer modulo 1e9+7.

Given below is the pictorial representation of the rectangle and restricted sub-rectangle:

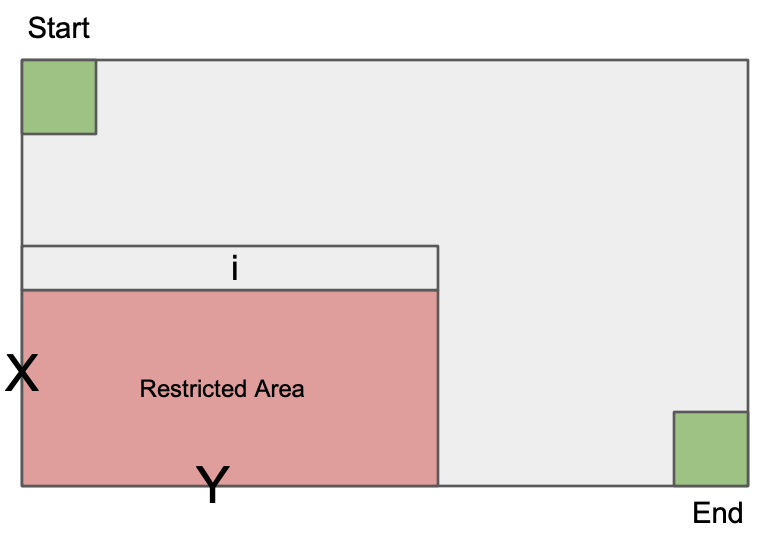
The value of i ranges from 1 to Y.

Examples:

Input: M = 3, N = 2, X = 1, Y = 1
Output: 2
Explanation: Only possible movies are RDD or DRD where R means Right and D means Down

Input: M = 8, N = 7, X = 2, Y = 4
Output: 1344

Input: M = 8, N = 7, X = 2, Y = 7
Output: 0
Explanation: The destination cell itself is restricted. Hence there is no way to reach there.

Approach: This can be solved with the following idea:

Suppose the obstacle starts at the Kth row and ends at the Lth column. The total number of combinations to reach from starting cell to end cell is ^(M+N-2)C_(M-1) as there are total M-1+N-1 moves out of which M-1 moves are to be selected. Then subtract the number of moves that lead the person into the restricted area. The restricted moves will be going into the restricted area down and moving inside the restricted area. The total combination for going into the restricted area will be due to DOWN movement going from non restricted row to a restricted row and the total moves will be column dependent for a range 1 ≤ i ≤ y and will be ^(M-X-1-i-1)C_(i-1). 

ANS = ^m+n−2C_m−1 − [ ^{m−x−1+i−1}C_m−x−1 + ^x−1+n−iC_x−1 ]

Steps involved in the code:

• First, calculate the factorial of the numbers with modulo inverse and also the inverse of the factorial under the same modulo. This can be done using Compute n! under modulo p
• Implement the nCr function by using binary exponentiation for fast power calculation. As we want the answer to be under modulo P use Fermat’s little theorem.
• Now find the total number of ways to reach the end block without the restricted area and let that be stored in res.
• Create a loop that runs from 1 to y with variable i and subtract for each i the combination discussed in step 8 and 9 of the efficient approach. That is subtracted from the res variable and those are the product of ^(M-X-1-i-1)C_(i-1) and ^(X-1+N-i)C_(X-1).
• The remaining number in the res variable will be the answer.

Below is the code for the given approach:

C++

// C++ program for the above approach

#include <bits/stdc++.h>
using namespace std;

// Maximum size of M+N
long long N = 200004;
const long long mod = 1e9 + 7;

// Binary exponentiation to calculate n^m
// in O(logn) time
long long binpow(long long a, long long b)
{
    long long res = 1;
    while (b > 0) {
        if (b & 1)
            res = (res % mod * a % mod) % mod;
        a = (a % mod * a % mod) % mod;
        b >>= 1;
    }
    return res % mod;
}

// Precalculate the factorial of numbers
// till N
void countFactorial(vector<long long>& fact)
{
    // Factorial of 0 = 1
    fact[0] = 1;

    // F[i] = F[i-1]*i
    for (int i = 1; i <= N; i++) {
        fact[i] = (fact[i - 1] % mod * i % mod) % mod;
    }
}

// Calculate inverse till N for nCr%p

void countInverse(vector<long long>& inv,
                  vector<long long> fact)
{

    // Inverse 0 = 1
    inv[0] = 1;

    inv[N] = binpow(fact[N], mod - 2);

    for (int i = N - 1; i > 0; i--) {
        inv[i] = (inv[i + 1] % mod * (i + 1) % mod) % mod;
    }
}

// Function to calculate nCr%p using DP
// or Fermat's Little Theorem
long long nCr(long long n, long long r,
              vector<long long> inv, vector<long long> fact)
{
    return (fact[n] % mod * inv[r] % mod * inv[n - r] % mod)
           % mod;
}

// Function to calculate number of ways
// to reach destination cell
long long countNumberOfWays(long long m, long long n,
                            long long x, long long y,
                            vector<long long> inv,
                            vector<long long> fact)
{

    // Total number of ways to reach
    // destination if there is no
    // restricted area
    long long res = nCr(m + n - 2, m - 1, inv, fact);

    // Traverse along the penultimate
    // row of restricted area
    // The first subrectangle
    for (int i = 1; i <= y; i++) {

        // Subtract the possibilities of
        // entering restricted area
        res -= (nCr(m - x - 1 + i - 1, m - x - 1, inv, fact)
                % mod * nCr(x - 1 + n - i, x - 1, inv, fact)
                % mod)
               % mod;

        // Add the mod id modulos
        // operation gives negative answer
        // due to subtraction
        res = (res + mod) % mod;
    }

    // Final answer return
    return res;
}

// Driver Code
int main()
{
    vector<long long> fact(200005);
    vector<long long> inv(200005);

    countFactorial(fact);
    countInverse(inv, fact);

    long long m = 8, n = 7, x = 2, y = 4;

    // Function call
    long long ans
        = countNumberOfWays(m, n, x, y, inv, fact);
    cout << ans << "\n";

    return 0;
}

Java

// JAVA program for the above approach

import java.util.*;

public class GFG {

    // Maximum size of M+N
    static long N = 200004;
    static final long mod = 1000000007;

    // Binary exponentiation to calculate n^m
    // in O(logn) time
    static long binpow(long a, long b)
    {
        long res = 1;
        while (b > 0) {
            if ((b & 1) != 0)
                res = (res % mod * a % mod) % mod;
            a = (a % mod * a % mod) % mod;
            b >>= 1;
        }
        return res % mod;
    }

    // Precalculate the factorial of numbers
    // till N
    static void countFactorial(long[] fact)
    {
        // Factorial of 0 = 1
        fact[0] = 1;

        // F[i] = F[i-1]*i
        for (int i = 1; i <= N; i++) {
            fact[i] = (fact[i - 1] % mod * i % mod) % mod;
        }
    }

    // Calculate inverse till N for nCr%p
    static void countInverse(long[] inv, long[] fact)
    {
        // Inverse 0 = 1
        inv[0] = 1;

        inv[(int)N] = binpow(fact[(int)N], mod - 2);

        for (int i = (int)N - 1; i > 0; i--) {
            inv[i]
                = (inv[i + 1] % mod * (i + 1) % mod) % mod;
        }
    }

    // Function to calculate nCr%p using DP
    // or Fermat's Little Theorem
    static long nCr(long n, long r, long[] inv, long[] fact)
    {
        return (fact[(int)n] % mod * inv[(int)r] % mod
                * inv[(int)(n - r)] % mod)
            % mod;
    }

    // Function to calculate number of ways
    // to reach destination cell
    static long countNumberOfWays(long m, long n, long x,
                                  long y, long[] inv,
                                  long[] fact)
    {

        // Total number of ways to reach
        // destination if there is no
        // restricted area
        long res = nCr(m + n - 2, m - 1, inv, fact);

        // Traverse along the penultimate
        // row of restricted area
        // The first subrectangle
        for (int i = 1; i <= y; i++) {

            // Subtract the possibilities of
            // entering restricted area
            res -= (nCr(m - x - 1 + i - 1, m - x - 1, inv,
                        fact)
                    % mod
                    * nCr(x - 1 + n - i, x - 1, inv, fact)
                    % mod)
                   % mod;

            // Add the mod id modulos
            // operation gives negative answer
            // due to subtraction
            res = (res + mod) % mod;
        }

        // Final answer return
        return res;
    }

    // Driver Code
    public static void main(String[] args)
    {
        long[] fact = new long[200005];
        long[] inv = new long[200005];

        countFactorial(fact);
        countInverse(inv, fact);

        long m = 8, n = 7, x = 2, y = 4;

        // Function call
        long ans = countNumberOfWays(m, n, x, y, inv, fact);
        System.out.println(ans);
    }
}

C#

using System;

public class GFG {
    // Maximum size of M+N
    static int N = 200004;
    const int mod = 1000000007;

    // Binary exponentiation to calculate n^m
    // in O(logn) time
    static int Binpow(int a, int b)
    {
        int res = 1;
        while (b > 0) {
            if ((b & 1) == 1)
                res = (int)((1L * res * a) % mod);
            a = (int)((1L * a * a) % mod);
            b >>= 1;
        }
        return res % mod;
    }

    // Precalculate the factorial of numbers
    // till N
    static void CountFactorial(int[] fact)
    {
        // Factorial of 0 = 1
        fact[0] = 1;

        // F[i] = F[i-1]*i
        for (int i = 1; i <= N; i++) {
            fact[i] = (int)((1L * fact[i - 1] * i) % mod);
        }
    }

    // Calculate inverse till N for nCr%p
    static void CountInverse(int[] inv, int[] fact)
    {
        // Inverse 0 = 1
        inv[0] = 1;

        inv[N] = Binpow(fact[N], mod - 2);

        for (int i = N - 1; i > 0; i--) {
            inv[i]
                = (int)((1L * inv[i + 1] * (i + 1)) % mod);
        }
    }

    // Function to calculate nCr%p using DP
    // or Fermat's Little Theorem
    static int NCr(int n, int r, int[] inv, int[] fact)
    {
        return (
            int)((1L * fact[n] * inv[r] % mod * inv[n - r])
                 % mod);
    }

    // Function to calculate the number of ways
    // to reach the destination cell
    static int CountNumberOfWays(int m, int n, int x, int y,
                                 int[] inv, int[] fact)
    {
        // Total number of ways to reach
        // the destination if there is no
        // restricted area
        int res = NCr(m + n - 2, m - 1, inv, fact);

        // Traverse along the penultimate
        // row of the restricted area
        // The first subrectangle
        for (int i = 1; i <= y; i++) {
            // Subtract the possibilities of
            // entering the restricted area
            res = (res
                   - (int)((1L
                            * NCr(m - x - 1 + i - 1,
                                  m - x - 1, inv, fact)
                            % mod
                            * NCr(x - 1 + n - i, x - 1, inv,
                                  fact))
                           % mod)
                   + mod)
                  % mod;
        }

        // Final answer return
        return res;
    }

    // Driver Code
    static void Main()
    {
        int[] fact = new int[200005];
        int[] inv = new int[200005];

        CountFactorial(fact);
        CountInverse(inv, fact);

        int m = 8, n = 7, x = 2, y = 4;

        // Function call
        int ans = CountNumberOfWays(m, n, x, y, inv, fact);
        Console.WriteLine(ans);

        // Uncomment the below line to see the result
        // Console.ReadLine();
    }
}

JavaScript

const mod = BigInt(1e9 + 7);

// Binary exponentiation to calculate a^b % mod
function binpow(a, b) {
    let res = BigInt(1);
    while (b > 0n) {
        if (b & 1n) {
            res = (res * a) % mod;
        }
        a = (a * a) % mod;
        b >>= 1n;
    }
    return res % mod;
}

// Precalculate the factorial of numbers till N
function countFactorial() {
    const fact = [BigInt(1)];

    // F[i] = F[i-1]*i
    for (let i = 1; i <= 200004; i++) {
        fact[i] = (fact[i - 1] * BigInt(i)) % mod;
    }
    return fact;
}

// Calculate inverse till N for nCr % mod
function countInverse(fact) {
    const inv = [BigInt(1)];

    inv[200004] = binpow(fact[200004], mod - 2n);

    for (let i = 200003; i >= 0; i--) {
        inv[i] = (inv[i + 1] * BigInt(i + 1)) % mod;
    }

    return inv;
}

// Function to calculate nCr % mod using DP or Fermat's Little Theorem
function nCr(n, r, inv, fact) {
    return (
        (fact[n] * inv[r] * inv[n - r]) % mod
    );
}

// Function to calculate number of ways to reach destination cell
function countNumberOfWays(m, n, x, y, inv, fact) {
    // Total number of ways to reach destination if there is 
    // no restricted area
    let res = nCr(m + n - 2, m - 1, inv, fact);

    // Traverse along the penultimate row of restricted area
    // The first subrectangle
    for (let i = 1; i <= y; i++) {
        // Subtract the possibilities of entering restricted area
        res -= (
            (nCr(m - x - 1 + i - 1, m - x - 1, inv, fact) *
                nCr(x - 1 + n - i, x - 1, inv, fact)) % mod
        );

        // Add the mod if modulo operation gives negative answer 
        // due to subtraction
        res = (res + mod) % mod;
    }

    // Final answer return
    return res;
}

// Driver Code
function main() {
    const fact = countFactorial();
    const inv = countInverse(fact);

    const m = 8;
    const n = 7;
    const x = 2;
    const y = 4;

    // Function call
    const ans = countNumberOfWays(m, n, x, y, inv, fact);
    console.log(ans.toString());
}

main();

Python3

# Python code for the above approach

# Maximum size of M+N
N = 200004
mod = int(1e9 + 7)

# Binary exponentiation to calculate a^b % mod
def binpow(a, b):
    res = 1
    while b > 0:
        if b & 1:
            res = (res % mod * a % mod) % mod
        a = (a % mod * a % mod) % mod
        b >>= 1
    return res % mod

# Precalculate the factorial of numbers till N
def countFactorial(fact):
    # Factorial of 0 = 1
    fact[0] = 1

    # F[i] = F[i-1]*i
    for i in range(1, N+1):
        fact[i] = (fact[i - 1] % mod * i % mod) % mod

# Calculate inverse till N for nCr % mod
def countInverse(inv, fact):
    # Inverse 0 = 1
    inv[0] = 1

    inv[N] = binpow(fact[N], mod - 2)

    for i in range(N-1, 0, -1):
        inv[i] = (inv[i + 1] % mod * (i + 1) % mod) % mod

# Function to calculate nCr % mod using DP or Fermat's Little Theorem
def nCr(n, r, inv, fact):
    return (fact[n] % mod * inv[r] % mod * inv[n - r] % mod) % mod

# Function to calculate number of ways to reach destination cell
def countNumberOfWays(m, n, x, y, inv, fact):
    # Total number of ways to reach destination if there is 
    # no restricted area
    res = nCr(m + n - 2, m - 1, inv, fact)

    # Traverse along the penultimate row of restricted area
    # The first subrectangle
    for i in range(1, y + 1):
        # Subtract the possibilities of entering restricted area
        res -= (nCr(m - x - 1 + i - 1, m - x - 1, inv, fact) % mod * 
                nCr(x - 1 + n - i, x - 1, inv, fact) % mod) % mod

        # Add the mod id modulos operation gives negative answer 
        # due to subtraction
        res = (res + mod) % mod

    # Final answer return
    return res

# Driver Code
if __name__ == "__main__":
    fact = [0] * 200005
    inv = [0] * 200005

    countFactorial(fact)
    countInverse(inv, fact)

    m = 8
    n = 7
    x = 2
    y = 4

    # Function call
    ans = countNumberOfWays(m, n, x, y, inv, fact)
    print(ans)

Output

1344

Time Complexity: O(N)
Auxiliary Space: O(N)