Matrix Operations are the operations that are operated on the matrix. Matrix Operation includes operations such as Addition of Matrix, Subtraction of Matrix, Multiplication of Matrix, etc, and others. These operations are very b useful for solving various problems of matrices and help us to find the transpose, inverse, rank, and others of the matrix. These operations help us to combine two or matrices.
In this article, we will learn about, Matrix Operations, Examples, and others in detail.
What are Matrix Operations?
Matrix operations are the operations that are used to combine various matrices to form a single matrix. The operations such as addition, subtraction, and multiplication are easily performed on the matrix. These matrix operations are very useful to solve matrix problems and to find the transpose and the inverse of the matrix.
Various matrix operations that are used to solve matrix problems are,
- Addition of Matrix
- Subtraction of Matrix
- Scaler Multiplication of Matrix
- Multiplication of Matrix
Now let’s learn about all the operations in detail.
Addition of Matrices
As we add two numbers we can easily add two matrices. The only thing we have to note is that the order of both the matrices that are to be added must be the same. That is to add two matrices we have to make sure that they are of the same order and then each element of the first matrix adds with each element of the second matrix to get a single matrix and thus the addition operation gets completed.
For any matrix A = 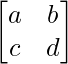 and matrix B =
and matrix B = 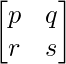 the sum of the matrix A and matrix B is C matrix then,
the sum of the matrix A and matrix B is C matrix then,
C = A + B = 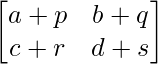
Example: Take three matrices A, B, and C of order 2×2, 2×2, and 3×3 respectively.
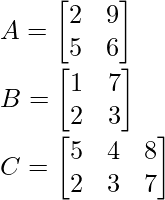
Find the sum of (A+B) and (A+C)
Solution:
Matrix A and Matrix B can be easily added as their order is the same. The addition of matrix A and matrix B is found as,
A + B = P = 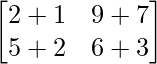
P = 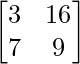
Matrix A and matrix C can not be added as their order is not the same.
Properties of Matrix Addition
There are various properties associated with matrix addition that are, for matrices A, B, and C of the same order, then
- Commutative Law: A + B = B + A
- Associative Law: (A + B) + C = A + (B + C)
- Identity of Matrix: A + O = O + A = A, where O is a zero matrix which is the Additive Identity of Matrix
- Additive Inverse: A + (-A) = O = (-A) + A, where (-A) is obtained by changing the sign of every element of A, which is the additive inverse of the matrix.
Subtraction of Matrices
As we add two matrices e can also easily subtract two matrices. The only thing we have to note is that the order of both the matrices that are to be subtracted must be the same. That is to subtract two matrices we have to make sure that they are of the same order and then each element of the first matrix is subtracted with each element of the second matrix to get a single matrix and thus the subtraction operation gets completed.
For any matrix A = 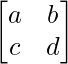 and matrix B =
and matrix B = 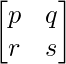 the difference of the matrix A and matrix B is C matrix then,
the difference of the matrix A and matrix B is C matrix then,
C = A – B = 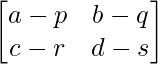
Example: For matrices A and B subtract the matrix B from matrix A
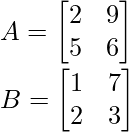
Solution:
Matrix A and Matrix B can be easily subtracted as their order is the same. The subtraction of matrix A and matrix B is found as,
A – B = P = 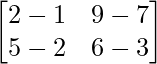
P = 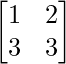
Scalar Multiplication of Matrices
For any matrix A = [aij]m×n if we multiply the matrix A with any scaler (say k) then the scaler is multiplied by each element of the matrix and this is called the scalar multiplication of matrices.
For any matrix A = 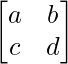 if it is multiplied by any scaler k then,
if it is multiplied by any scaler k then,
kA = 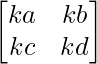
Properties of Scalar Multiplication
For any matrices, A and B of the same order and λ and μ are any two scalars, then,
- λ(A + B) = λA + λB
- (λ + μ)A = λA + μA
- λ(μA) = (λμA) = μ(λA)
- (-λA) = -(λA) = λ(-A)
Multiplication of Matrix
Matrix multiplication is the operation that helps us to multiply two matrices. This is different from algebraic multiplication and not all the matrices can be multiplied. Only those matrices can be multiplied where the number of columns in the first is equal to the number of rows in the second, i.e for matrix Am×n and matrix Bn×p the multiplication is possible for any other matrices where the column of the first matrix is not equal to the row in the second matrix the multiplication is not possible.
Also, the multiplication of the matrices is not commutative, i.e. if matrix A and matrix B are taken then A×B ≠ B×A.
Learn more about, Matrix Multiplication
Transpose Operation of a Matrix
Tramspose operation of a matrix is used to find the transpose of any matrix. Transpose of any matrix is a matrix in which the rows of the matrix are changed to the column of the matrix and the column of the matrix is changed to the rows of the matrix. Suppose we have a matrix A of order m×n such that A =[ij]m×n then the transpose of matrix A is represented as (A)T and its value is,
(A)T = [ji]n×m
Learn more about, Transpose of a Matrix
Inverse Operation of a Matrix
For any matrix A its inverse is found only when A is a square matrix and its determinant is equal to 1, i.e.
A = [ij]n×n and |A| = 1
Now the inverse of a matrix A is a matrix that on multiplying with the matrix A results in the identity matrix. It is represented as (A)-1, and the inverse operation of the matrix is an operation that helps us to find the inverse of the matrix. For any square matrix A we know that,
A×(A)-1 = I
where “I” is the identity matrix of the same order as A.
Read More,
Solved Examples on Matrix Operations
Example 1: Find the sum of matrix A and B when,
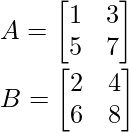
Solution:
Matrix A and Matrix B can be easily added as their order is the same. The addition of matrix A and matrix B is found as,
A + B = P = 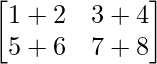
P = 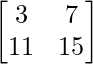
Example 2: Find (A – B) when,
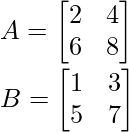
Solution:
Matrix A and Matrix B can be easily subtracted as their order is the same. The value of (A-B) is found as,
(A – B) = P = 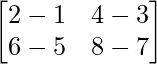
P = 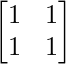
Example 2: Find the transpose of matrix A
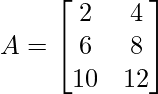
Solution:
Transpose of matrix A is the matrix in which the rows of matrix A are its column and the column are its rows.
Tranpose of matrix A is represented as, (A)T
(A)T= 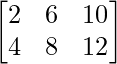
FAQs on Matrix Operation
1. What Product of a Matrix with an Identity Matrix?
The product of any matrix with the identity matrix is the same matrix itself. Suppose we have a matrix A and an identity matrix I of the same order, then
A × I = I × A = A
2. What is a Singular Matrix?
Any square matrix whose value of the determinant is one is called the singular matrix, i.e. for any square matrix A to be singular,
|A| = 1
3. Is Matrix Addition Commutative?
Yes, matrix addition holds commutative law, i.e. for any two matrices A and B that can be added,
A + B = B + A
4. Is Matrix Multiplication Commutative?
No, matrix multiplication does not hold commutative law, i.e. for any two matrices A and B that can be multiplied,
A × B ≠ B × A
5. What are Three Important Matrix Operations?
The three important matrix operations are,
- Addition of Matrix
- Subtraction of Matrix
- Multiplication of Matrix
Share your thoughts in the comments
Please Login to comment...