Determinant of a Matrix is defined as the function that gives the unique output (real number) for every input value of the matrix. Determinant of the matrix is considered the scaling factor that is used for the transformation of a matrix. It is useful for finding the solution of a system of linear equations, the inverse of the square matrix, and others. The determinant of only square matrices exists.
Determinant of Matrix Calculator
A determinant of a matrix calculator is a tool used to compute the determinant of a given matrix quickly and accurately.
Definition of Determinant of Matrix
Determinant of a Matrix is defined as the sum of products of the elements of any row or column along with their corresponding co-factors. Determinant is defined only for square matrices.
Determinant of any square matrix of order 2×2, 3×3, 4×4, or n × n, where n is the number of rows or the number of columns. (For a square matrix number of rows and columns are equal). Determinant can also be defined as the function which maps every matrix with the real numbers.
For any set S of all square matrices, and R the set of all numbers the function f, f: S → R is defined as f (x) = y, where x ∈ S and y ∈ R, then f (x) is called the determinant of the input matrix.
Symbol of Determinant
Let’s take any square matrix A, then the determinant of A is denoted as det A (or) |A|. Determinant is also denoted by the symbol Δ.
Minor of Element of Matrix
Minor is required to find determinant for single elements (every element) of the matrix. They are the determinants for every element obtained by eliminating the rows and columns of that element. If the matrix given is:

Minor of a12 will be the determinant:
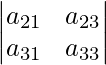
Question: Find the Minor of element 5 in the determinant 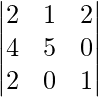
Answer:
The minor of element 5 will be the determinant of 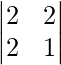
Calculating the determinant, the minor is obtained as:
(2 × 1) – (2 × 2) = -2
Cofactors of Element of Matrix
Cofactors are related to minors by a small formula, for an element aij, the cofactor of this element is Cij and the minor is Mij then, the cofactor can be written as:
Cij = (-1)i+jMij
Question: Find the cofactor of the element placed in the first row and second column of the determinant:

Answer:
In order to find out the cofactor of the first row and second column element i.e the cofactor for 1. First find out the minor for 1, which will be:
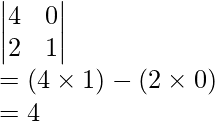
M12 = 4
Now, applying the formula for cofactor:
C12 = (-1)1 + 2M12
C12 = (-1)3 × 4
C12 = -4
Adjoint of a Matrix
The Adjoint of a matrix for order n can be defined as the transpose of its cofactors. For a matrix A:
Adj. A = [Cij]n×nT
Transpose of a Matrix
Transpose of a Matrix A is denoted as AT or A’. It is clear that the vertical side in the matrix is known as a column and the horizontal side is known as a row, Transposing a Matrix means replacing the Rows with columns and Vice-Versa, since the Rows and Columns are changing, the Order of the Matrix also changes.
If a Matrix is given as A= [aij]m×n, then its Transpose will become
AT or A’ = [aji]n×m
Question: What will be the transpose of the Matrix A =
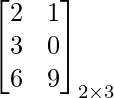
Answer:
Interchanging Rows and Columns, AT = 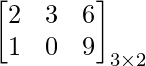
Determinant of a 1×1 Matrix
Let X = [a] be the matrix of order one, then its determinant is given by det(X) = a.
Determinant of 2×2 Matrix
The determinant of any 2×2 square matrix A = 
is calculated using the formula |A| = ad – bc.
Example: Find the Determinant of A =
Solution:
Determinant of A =  is calculated as,
is calculated as,
| A | = 
| A | = 3×3 – 2×2
= 9 – 4
= 5
Determinant of a 3×3 Matrix
Determinant of a 3×3 Matrix is determined by expressing it in terms of 2nd-order determinants. It can be expanded either along rows(R1, R2 or R3) or column(C1, C2 or C3). Consider a matrix A of order 3×3
det(A) = a11(a22a33 – a23a32) – a12(a21a33 – a23a31) + a13(a21a32 – a22a31)
How to Find Determinant of 3×3 Matrix
For calculating the Determinant of 3×3 Matrix use the following step:
Step 1: Multiply the first element a11 of row R1 with (-1)(1 + 1)[(-1)sum of suffixes in a11] and with the second order determinant obtained by deleting the elements of row R1 and C1 of A as a11 lies in R1 and C1. 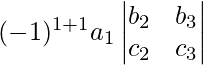
Step 2: Similarly, multiply the second element of the first rowR1, with the determinant obtained after deleting the first row and second column. 
Step 3: Multiply the third element of row R1 with the determinant obtained after deleting the first row and third column. 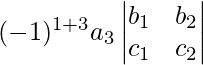
Step 4: Now the expansion of the determinant of A, that is |A| can be written as |A| = 
Similarly, in this way, we can expand it along any row and any column.
Example: Evaluate the determinant det(A) = 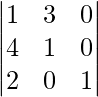
Solution:
We see that the third column has most number of zeros, so it will be easier to expand along that column.
det(A) = 
Determinant of 4×4 Matrix
Determining the determinant of a 4×4 matrix involves more complex methods such as expansion by minors or Gaussian elimination. These techniques require breaking down the matrix into smaller submatrices and recursively finding their determinants. While there isn’t a direct formula like Sarrus’ Rule for 3×3 matrices, the process involves systematic calculations based on the properties of determinants.
How to Find Determinant of 4×4 Matrix
By following these step-by-step instructions, you can efficiently find the determinant of a 4×4 matrix using cofactor expansion:
- Identify a Row or Column for Expansion: Choose a row or column along which you will perform cofactor expansion. While any row or column can be chosen, it’s often easiest to select the row or column with the most zeros to simplify calculations.
- Calculate Cofactors: For each element aij of the chosen row or column, calculate its cofactor Cij. To find the cofactor, follow these steps:
- For each element aij, find the determinant of the 3×3 submatrix formed by eliminating the row and column containing aij.
- Apply the alternating sign pattern: positive for elements in even positions and negative for elements in odd positions.
- Multiply the determinant of the 3×3 submatrix by the appropriate sign to obtain the cofactor Cij.
- Multiply Elements by Their Cofactors: Multiply each element of the chosen row or column by its corresponding cofactor.
- Sum Up the Results: Sum up the products obtained in the previous step. This will give you the determinant of the 4×4 matrix.
- Repeat for Other Rows or Columns (Optional): If needed, repeat the process of cofactor expansion along other rows or columns until you find the determinant. However, it’s generally most efficient to choose the row or column with the most zeros initially.
- Verify the Determinant: Double-check your calculations and verify the determinant obtained.
- Result: The final result is the determinant of the 4×4 matrix.
Determinant of Identity Matrix
An identity matrix is a square matrix in which all the elements of the main diagonal are ones, and all other elements are zeros. For example, a 3×3 identity matrix looks like this:

The determinant of an identity matrix of any size is always 1. This property can be understood intuitively by considering that the identity matrix represents a transformation that leaves vectors unchanged when multiplied by it. Since the determinant measures how a matrix scales the space, the determinant of an identity matrix, which doesn’t scale the space at all, is 1.
Mathematically, we can express this as:
det (I) = 1
Determinant of Symmetric Matrix
A symmetric matrix is a square matrix that is equal to its transpose. In other words, if A is a symmetric matrix, then A = AT. Symmetric matrices have several interesting properties, one of which is that their determinants remain unchanged under transpose.
Hence, for a symmetric matrix A, we have:
det(A) = det(AT)
This property simplifies the computation of determinants for symmetric matrices since you can work with either the original matrix or its transpose, whichever is more convenient.
Determinant of Skew-Symmetric Matrix
A skew-symmetric (or antisymmetric) matrix is a square matrix whose transpose is equal to its negative. In other words, if A is a skew-symmetric matrix, then A = −AT. Skew-symmetric matrices have interesting properties, one of which is that their determinants have specific values based on the order of the matrix.
For skew-symmetric matrices of odd order, the determinant is always 0. This is because the determinant of a skew-symmetric matrix is always the square of its eigenvalues, and a non-zero square is always positive. Since the order of the matrix is odd, at least one eigenvalue must be zero, resulting in a determinant of 0.
For skew-symmetric matrices of even order, the determinant is a non-zero value, which can be calculated based on the elements of the matrix. However, determining the exact value typically involves more complex methods such as cofactor expansion or using properties of determinants.
Determinant of Inverse Matrix
To understand the determinant of the inverse matrix, let’s first define what the inverse of a matrix is.
The inverse of a square matrix A, denoted as A−1, is a matrix such that when it’s multiplied by A, the result is the identity matrix I. Mathematically, if A⋅A−1 = I, then A−1 is the inverse of A.
Now, the determinant of the inverse matrix, denoted as det(A−1), is related to the determinant of the original matrix A. Specifically, it can be expressed by the formula:
det(A−1) = 1/det(A)
This formula illustrates an important relationship between the determinants of a matrix and its inverse. If the determinant of A is non-zero, meaning det(A)≠0, then the inverse matrix exists, and its determinant is the reciprocal of the determinant of A. Conversely, if det(A)=0, the matrix A is said to be singular, and it does not have an inverse.
Here are some key points about the determinant of the inverse matrix:
- Non-Singular Matrices: For non-singular matrices (those with non-zero determinants), their inverses exist, and the determinant of the inverse is the reciprocal of the determinant of the original matrix.
- Singular Matrices: Singular matrices (those with zero determinants) do not have inverses. Attempting to find the inverse of a singular matrix results in an undefined or non-existent inverse.
- Geometric Interpretation: The determinant of a matrix measures how it scales the space. Similarly, the determinant of the inverse matrix measures the scaling effect of the inverse transformation. If the original transformation expands the space, its inverse contraction will be inversely proportional, and vice versa.
Determinant of Orthogonal Matrix
An orthogonal matrix is a square matrix whose rows and columns are orthonormal vectors, meaning that the dot product of any two distinct rows or columns equals zero, and the dot product of each row or column with itself equals one. Mathematically, if A is an orthogonal matrix, then AT⋅A=I, where AT denotes the transpose of A and I represents the identity matrix.
The determinant of an orthogonal matrix has a special property:
det (A) = ±1
The determinant of an orthogonal matrix is either +1+1 or −1−1. This property arises from the fact that the determinant represents the scaling factor of the matrix transformation. Since orthogonal transformations preserve lengths, the determinant must be either positive (for preserving orientation) or negative (for reversing orientation).
The determinant of an orthogonal matrix being +1+1 implies that the transformation preserves orientation, while a determinant of −1−1 indicates a transformation that reverses orientation.
Physical Significance of Determinant
Consider a 2D matrix, each column of this matrix can be considered as a vector on the x-y plane. So, the determinant between two vectors on a 2d plane gives us the area enclosed between them. If we extend this concept, in 3D the determinant will give us the volume enclosed between two vectors.

Area enclosed between two vectors in 2D
Laplace’s formula, is used to expressed the determinant of a matrix in terms of the minors of the matrix.
If An×n is the given square matrix and Cij is the cofactor of Aij the solving for any row i or column j
det (A) = 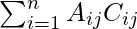
Properties of Determinants of Matrix
Various Properties of the Determinants of the square matrix are discussed below:
- Reflection Property: Value of the determinant remains unchanged even after rows and columns are interchanged. That determinant of a matrix and its transpose remains the same.
- Switching Property: If any two rows or columns of a determinant are interchanged, then the sign of the determinant changes.
- Scalar Multiplication Property: If each element in a row or column of a matrix A is multiplied by a scalar k, then the determinant of the resulting matrix is k times the determinant of A. Mathematically, if B is the matrix obtained by multiplying each element of a row or column of A by k, then det(B) = k⋅det(A).
- Additivity Property: The determinant of the sum of two matrices A and B is equal to the sum of their determinants. Symbolically, det(A+B) = det(A) + det(B). However, this property applies only if the matrices have the same dimensions.
- Multiplicative Property: The determinant of the product of two matrices A and B is equal to the product of their determinants. Symbolically, det(AB) = det(A)⋅det(B). However, this property holds true only for square matrices.
- Determinant of Transpose: The determinant of a matrix A is equal to the determinant of its transpose AT. Mathematically, det(A) = det(AT).
Example: 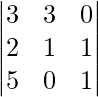
Solution:
det. A = [3×{(1×1)-(0×1)}]-[3×{(2×1)-(5×1)}]+[0×{(2×0)-(5×1)}]
= {3×(1-0)}-{3×(2-5)+0
= [3-{3(-3)}+0]
= (3+9)
=12
Now, Interchanging Row 1 with Row 2, determinant will be:
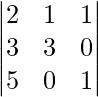
det. A = [2×{(3×1)-(0×0)}]-[1×{(3×1)-(5×0)}]+[1×{(3×0)-(5×3)}]
= (6-3-15)
= -12
- Repetition Property/Proportionality Property: If any two rows or any two columns of a determinant are identical, then the value of the determinant becomes zero.
- Scalar Multiple Property: If each element of a row (or a column) of a determinant is multiplied by a constant k, then its value gets multiplied by k

- Sum Property: If some or all elements of a row or column can be expressed as the sum of two or more terms, then the determinant can also be expressed as the sum of two or more determinants.

Solved Questions on Determinant of Matrix
Question 1: If x, y, and z are different. and A =  , then show that 1 + xyz = 0.
, then show that 1 + xyz = 0.
Solution:
Using Sum Property

On solving this determinant and expanding it,
A = (1 + xyz)(y- x)(z-y)(z-x)
Since it’s given in the question, that all x, y and z have different values and A =0. So the only term that can be zero is 1 + xyz.
Hence, 1 + xyz = 0
Question 2: Evaluate  .
.
Solution:
Using Scalar Multiple Property and Repetition Property

Question 3: Evaluate the determinant 
Solution:
Using Proportionality Property
Two of the rows of the matrix are identical.
So, 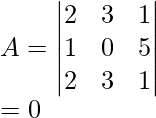
FAQs on Determinant of Matrix
What is meant by the determinant formula?
For any 3×3 matrix A =  the shortcut formula for computing its determinant is:
the shortcut formula for computing its determinant is:
|A| = a (ei − fh) − b (di − fg) + c (dh − eg)
Can determinant of any matrix be negative?
Yes, the determinant of any matrix can be negative.
Can determinant of any matrix ever be equal to 0?
Yes, the determinant of any matrix can be zero if any one row or column of the matrix has all the zero values. It can also be zero if any two rows or columns of the matrix are equal.
How to find the determinant of matrix?
The determinant of any matrix can be found by using the following steps:
Step 1: Select any row or column of our choice.
Step 2: Calculate the cofactors of all the elements of the selected row or column
Step 3: The product of the elements of the row or column by their corresponding cofactors is found. The calculated product is added with alternate negative sign.
Share your thoughts in the comments
Please Login to comment...